5.2: Рівномірний розподіл
- Page ID
- 99944
Рівномірний розподіл є безперервним розподілом ймовірностей і стосується подій, які однаково ймовірні. При розробці проблем, які мають рівномірний розподіл, будьте обережні, якщо дані є включними або виключними з кінцевих точок.
Математичне твердження рівномірного розподілу дорівнює
\(f(x) = \frac{1}{b-a}\)для\(a \leq x \leq b\)
де\(a =\) найнижче значення\(x\)\(b =\) і найбільше значення\(x\).
Формули теоретичного середнього і стандартного відхилення
\(\mu=\frac{a+b}{2}\)і\(\sigma=\sqrt{\frac{(b-a)^{2}}{12}}\)
Вправа\(\PageIndex{1}\)
Дані, які слідують за кількістю пасажирів на 35 різних чартерних рибальських човнів. Середнє значення зразка = 7,9, а стандартне відхилення вибірки = 4,33. Дані слідують за рівномірним розподілом, де всі значення між нулем і 14 включно однаково вірогідні. Викладіть значення\(a\) і\(b\). Запишіть розподіл в належних позначеннях, і обчисліть теоретичне середнє і стандартне відхилення.
\ (\ індекс сторінки {1}\) «>| 1 | 12 | 4 | 10 | 4 | 14 | 11 |
| 7 | 11 | 4 | 13 | 2 | 4 | 6 |
| 3 | 10 | 0 | 12 | 6 | 9 | 10 |
| 5 | 13 | 4 | 10 | 14 | 12 | 11 |
| 6 | 10 | 11 | 0 | 11 | 13 | 2 |
-
Таблиця 5.1
Приклад\(\PageIndex{2}\)
Кількість часу, в хвилинах, яке людина повинна чекати автобуса, рівномірно розподіляється між нулем і 15 хвилинами включно.
а. яка ймовірність того, що людина чекає менше 12,5 хвилин?
- Відповідь
-
а. нехай\(X\) = кількість хвилин, які людина повинна чекати автобуса. \(a = 0\)і\(b = 15\). \(X \sim U(0, 15)\). Запишіть функцію щільності ймовірності. \(f(x) = \frac{1}{15-0}=\frac{1}{15}\)для\(0 \leq x \leq 15\).
Знайти\(P(x < 12.5)\). Намалюйте графік.
\[P(x<k)=\text { (base) (height) }=(12.5-0)\left(\frac{1}{15}\right)=0.8333\nonumber\]
Імовірність того, що людина чекає менше 12,5 хвилин, становить 0,8333.
Малюнок 5.11
б. в середньому, скільки часу повинен чекати людина? Знайти середнє\(\mu\), і стандартне відхилення,\(\sigma\).
- Відповідь
-
б\(\mu=\frac{a+b}{2}=\frac{15+0}{2}=7.5\). В середньому людина повинна почекати 7,5 хвилин.
\(\sigma=\sqrt{\frac{(b-a)^{2}}{12}}=\sqrt{\frac{(15-\theta)^{2}}{12}}=4.3\). Стандартне відхилення становить 4,3 хвилини.
c Дев'яносто відсотків часу, час, який людина повинна чекати, падає нижче якого значення?
Примітка
Це просить 90-й процентиль.
- Відповідь
-
c. знайти 90-й процентиль. Намалюйте графік. Нехай\(k =\) 90-й процентиль.
\ (P (x<k) >
\(0.90=(k)\left(\frac{1}{15}\right)\)
\(k=(0.90)(15)=13.5\)
90-й процентиль становить 13,5 хвилин. Дев'яносто відсотків часу людина повинна чекати не більше 13,5 хвилин.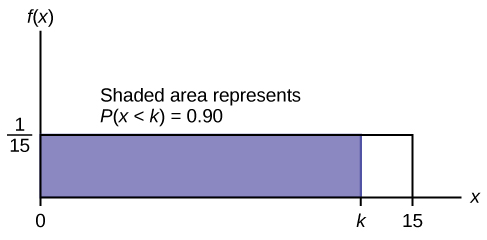 Малюнок\(\PageIndex{12}\)
Малюнок\(\PageIndex{12}\)
Вправа\(\PageIndex{2}\)
Загальна тривалість бейсбольних ігор у вищій лізі в сезоні 2011 рівномірно розподілена між 447 годин і 521 годин включно.
- Знайдіть\(a\)\(b\) і опишіть, що вони собою представляють.
- Напишіть дистрибутив.
- Знайдіть середнє і стандартне відхилення.
- Яка ймовірність того, що тривалість ігор для команди в сезоні 2011 року становить від 480 до 500 годин?
