4.4: Методи підрахунку

Last updated
Save as PDF

Page ID: 97505

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Бувають випадки, коли простір зразка або простір подій дуже великі, що його неможливо виписати. У такому випадку допомагає мати математичні інструменти для підрахунку розмірів вибіркового простору та простору подій. Ці інструменти відомі як методи підрахунку.

Визначення\(\PageIndex{1}\)

Правило множення в методах підрахунку

Якщо завдання 1 може бути виконано \(m_{1}\)способами, завдання 2 може бути виконано \(m_{2}\)способами, і так далі до завдання п виконуються \(m_{n}\)способами. Тоді кількість способів зробити завдання 1, 2,..., п разом буде \(m_{1}^{*} m_{2}^{*} \stackrel{\Delta *}{r} m_{n}\).

Приклад\(\PageIndex{1}\) multiplication rule in counting

У меню на вибір 3 салати, 8 основних страв і 5 десертів. Скільки можна різних страв, що складаються з одного салату, одного основного блюда, одного десерту?

Рішення

Є три завдання: підібрати салат, основну страву і десерт. Завдання салату можна виконати 3 способами, основне завдання страви можна виконати 8 способів, а десертну - 5 способів. Способи засолювання салату, основної страви та десерту:

\(\dfrac{3}{\text { salad }} \dfrac{8}{\text { main }} \dfrac{5}{\text { dessert }}=120\)різне харчування

Приклад\(\PageIndex{2}\) Multiplication rule in counting

Скільки трьох літер «слів» можна зробити з букв a, b і c без повторення букв? «Слово» - це просто впорядкована група букв. Це не повинно бути справжнім словом у словнику.

Рішення

Є три завдання, які необхідно виконати в цьому випадку. Завдання полягають в тому, щоб вибрати першу букву, потім другу, а потім третю букву. Перше завдання можна виконати 3 способами, так як є 3 букви. Друге завдання можна виконати 2 способами, так як перше завдання зайняло одну з букв. Третє завдання можна виконати 1 способом, так як перше і друге завдання зайняло дві букви. Є

\(\dfrac{3}{\text { first letter }} * \dfrac{2}{\text { second letter }} * \dfrac{1}{\text { third letter }}\)

Що таке

\(3^{*} 2^{*} 1=6\)

Ви також можете подивитися на це в деревоподібній діаграмі:

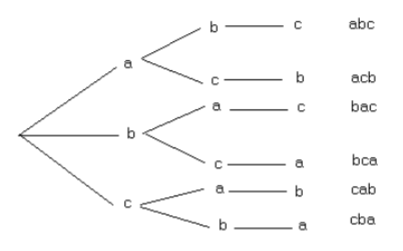Знімок екрана (72) .png — Малюнок\(\PageIndex{1}\): Діаграма дерева

Отже, існує 6 різних «слів».

У\(\PageIndex{2}\) прикладі рішення було знайдено за допомогою find\(3*2*1=6\). Багато проблем підрахунку припускають множення списку спадних чисел. Це називається факторіал. Для цього є спеціальний символ і спеціальна кнопка на вашому калькуляторі.

Визначення\(\PageIndex{2}\)

Факторіал

\(n !=n(n-1)(n-2) \cdots(3)(2)(1)\)

Як приклад:

\(5 !=5 * 4 * 3 * 2 * 1=120\)

\(8 !=8 * 7 * 6 * 5 * 4 * 3 * 2 * 1=40320\)

0 факторіал визначається як 0! =1 і 1 факторіал визначається як 1! =1.

Іноді ви намагаєтеся виділити r об'єктів із загальної кількості об'єктів. Кількість способів зробити це залежить від того, чи має значення порядок, який ви виберете об'єкти r, або якщо це не. наприклад, якщо ви намагаєтеся зателефонувати людині по телефону, ви повинні мати їх номер у правильному порядку. В іншому випадку ви телефонуєте комусь, кого не хотіли. При цьому має значення порядок чисел. Однак якщо ви вибирали випадкові числа для лотереї, не має значення, який номер ви виберете першим. Поки у вас є ті ж цифри, які вибирають люди лотереї, ви виграєте. У цьому випадку порядок не має значення. Перестановка - це розташування елементів з певним порядком. Ви використовуєте перестановки для підрахунку елементів, коли замовлення має значення. Коли замовлення не має значення, ви використовуєте комбінації. Комбінація - це розташування предметів, коли порядок не важливий. Коли ви робите проблему підрахунку, перше, що ви повинні запитати себе, це «чи має значення порядок?»

Визначення\(\PageIndex{3}\)

Формула перестановки

Підбір r об'єктів із загальної кількості об'єктів, коли порядок має значення

\(_{n} P_{r}=\dfrac{n !}{(n-r) !}\)

Визначення\(\PageIndex{4}\)

Комбінована формула

Вибір r об'єктів із загальної кількості об'єктів, коли замовлення не має значення

\(_{n} C_{r}=\dfrac{n !}{r !(n-r) !}\)

Приклад\(\PageIndex{3}\) calculating the number of ways

У клубі з 15 членами, скільки способів може бути обраний лист з 3 офіцерів, що складається з президента, віце-президента та секретаря/скарбника?

Рішення

У цьому випадку порядок має значення. Якщо ви вибираєте людину 1 для президента, особу 2 для віце-президента та особу 3 для секретаря/скарбника, у вас будуть різні офіцери, ніж якби ви вибрали людину 2 для президента, особу 1 для віце-президента та особу 3 для секретаря/скарбника. Це проблема перестановки з n = 15 і r = 3.

\(_{15} P_{3}=\dfrac{15 !}{(15-3) !}=\dfrac{15 !}{12 !}=2730\)

Приклад\(\PageIndex{4}\) calculating the number of ways

Припустимо, ви хочете вибрати 7 осіб з 20 осіб для участі в опитуванні. Скільки способів ви можете це зробити?

Рішення

У цьому випадку замовлення не має значення, так як ви хочете всього 7 осіб. Це комбінація з n = 20 і r=7.

\(_{20} C_{7}=\dfrac{20 !}{7 !(20-7) !}=\dfrac{20 !}{7 ! 13 !}=77520\)

Більшість калькуляторів мають кнопку факторіала на них, і багато хто також має функції комбінації та перестановки. R має команду комбінації.

Домашнє завдання

Вправа\(\PageIndex{1}\)

Ви збираєтеся на корисний обід, і перед вечерею потрібно вирішити, що ви хочете для салату, основної страви та десерту. У вас є 2 різні салати на вибір, 3 основні страви та 5 десертів. Скільки різних страв доступно?
Скільки різних телефонних номерів можливо в коді міста 928?
Ви відкриваєте магазин футболок. Ви можете мати довгі рукави або короткі рукави, три різні кольори, п'ять різних конструкцій та чотири різних розміру. Скільки різних сорочок ви можете зробити?
Каліфорнійський номерний знак має одну цифру, за якою йдуть три літери, за якими слідують три цифри. Скільки існує різних номерних знаків?
Знайти\(_{9} P_{4}\)
Знайти\(_{10} P_{6}\)
Знайти\(_{10} P_{5}\)
Знайти\(_{20} P_{4}\)
У вас є група з дванадцяти чоловік. Вам потрібно вибрати президента, скарбника і секретаря з дванадцяти. Скільки різних способів ви можете це зробити?
Бейсбольна команда має 25-чоловік реєстр. Порядок ватин налічує дев'ять чоловік. Скільки існує різних замовлень на ватин?
Урна містить п'ять червоних кульок, сім жовтих кульок і вісім білих кульок. Скільки різних способів ви можете вибрати дві червоні кулі?
Скільки способів можна вибрати сім чоловік з групи двадцяти?

Відповідь

1. 30 прийомів їжі

3. 120 сорочок

5. 3024

7. 252

9. 1320

11. 10

Джерела даних

Смерть аборигенів під вартою. (2013, 26 вересня). Отримано з http://www.statsci.org/data/oz/custody.html

Діяльність груп дельфінів. (2013, 26 вересня). Отримано з http://www.statsci.org/data/general/dolpacti.html

Уподобання автомобіля. (2013, 26 вересня). Отримано з http://www.statsci.org/data/oz/carprefs.html

Енциклопедія Титаніка. (2013, 09 листопада). Отримано з www.енциклопедіатітаніка.org/

Лепра: Кількість зареєстрованих випадків за країнами. (2013, 04 вересня). Отримано з http://apps.who.int/gho/data/node.main.A1639

Медісон, Дж. (2013, 15 жовтня). Аналіз розподілу кольорів M&M. Отримано з http://joshmadison.com/2007/12/02/mm...tion-analysis/