Skip to main content
LibreTexts - Ukrayinska

6.2: Стандартний нормальний розподіл

  1. Last updated
  2. Save as PDF
  • Page ID
    98534

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Z-результати

    Стандартний нормальний розподіл - це нормальний розподіл стандартизованих значень, званих z-scores. Z-оцінка вимірюється в одиницях стандартного відхилення.

    Визначення: Z-Score

    Якщо\(X\) є нормально розподіленою випадковою величиною і\(X \sim N(\mu, \sigma)\), то z -score дорівнює:

    \[z = \dfrac{x - \mu}{\sigma} \label{zscore}\]

    z -score говорить вам, скільки стандартних відхилень значення\(x\) вище (праворуч) або нижче (ліворуч від) середнього,\(\mu\). Значення\(x\) яких більші за середнє мають позитивні\(z\) -оцінки, а значення\(x\) яких менші за середнє мають негативні\(z\) -бали. Якщо\(x\) дорівнює середньому, то\(x\) має\(z\) -score нуль. Наприклад, якщо середнє значення нормального розподілу дорівнює п'яти, а стандартного відхилення - два, значення 11 - це три стандартні відхилення вище (або праворуч від) середнього. Розрахунок відбувається наступним чином:

    \[ \begin{align*} x &= \mu + (z)(\sigma) \\[5pt] &= 5 + (3)(2) = 11 \end{align*}\]

    Z -оцінка дорівнює трьом.

    Оскільки середнє значення для стандартного нормального розподілу дорівнює нулю, а стандартне відхилення дорівнює одиниці, то перетворення в Equation\ ref {zscore} дає розподіл\(Z \sim N(0, 1)\). Значення\(x\) походить від нормального розподілу із середнім\(\mu\) і стандартним відхиленням\(\sigma\).

    Z-оцінка вимірюється в одиницях стандартного відхилення.

    Приклад\(\PageIndex{1}\)

    Припустимо\(X \sim N(5, 6)\). Це говорить про те, що\(x\) це нормально розподілена випадкова величина із середнім\(\mu = 5\) і стандартним відхиленням\(\sigma = 6\). Припустимо\(x = 17\). Потім (через рівняння\ ref {zscore}):

    \[z = \dfrac{x-\mu}{\sigma} = \dfrac{17-5}{6} = 2 \nonumber\]

    Це означає, що\(x = 17\) це два стандартних відхилення (2\(\sigma\)) вище або праворуч від середнього\(\mu = 5\). Стандартне відхилення - це\(\sigma = 6\).

    Зверніть увагу, що:\(5 + (2)(6) = 17\) (Візерунок є\(\mu + z \sigma = x\))

    Тепер припустимо\(x = 1\). Потім:

    \[z = \dfrac{x-\mu}{\sigma} = \dfrac{1-5}{6} = -0.67 \nonumber\]

    (округлено до двох знаків після коми)

    Це означає,\(x = 1\) що\(0.67\) стандартні відхилення (\(–0.67\sigma\)) нижче або вліво від середнього\(\mu = 5\). Зверніть увагу, що: приблизно\(5 + (–0.67)(6)\) дорівнює одиниці (Це має візерунок\(\mu + (–0.67)\sigma = 1\))

    Підсумовуючи, коли\(z\) позитивний,\(x\) знаходиться вище або праворуч від,\(\mu\) а коли\(z\) негативний,\(x\) знаходиться ліворуч або нижче\(\mu\). Або,\(z\) коли\(x\) позитивний, більше\(\mu\), а коли\(z\)\(x\) негативний менше\(\mu\).

    Вправа\(\PageIndex{1}\)

    Що таке\(z\) -оцінка\(x\), коли\(x = 1\) і\(X \sim N(12, 3)\)?

    Відповідь

    \(z = \dfrac{1-12}{3} \approx -3.67\)

    Приклад\(\PageIndex{2}\)

    Деякі лікарі вважають, що людина може втратити п'ять фунтів, в середньому, за місяць, зменшуючи споживання жиру та послідовно займаючись фізичними вправами. Припустимо, втрата ваги має нормальний розподіл. Нехай\(X =\) кількість втраченої ваги (в фунтах) людиною за місяць. Використовуйте стандартне відхилення в два кілограми. \(X \sim N(5, 2)\). Заповніть заготовки.

    1. Припустимо, людина втратила десять кілограмів за місяць. The\(z\) -score, коли\(x = 10\) фунти є\(x = 2.5\) (перевірити). Цей\(z\) -оцінка говорить вам, що\(x = 10\) це ________ стандартні відхилення до ________ (праворуч або ліворуч) середнього _____ (Що таке середнє?).
    2. Припустимо, людина набрала три кілограми (негативна втрата ваги). Потім\(z =\) __________. Цей\(z\) -оцінка говорить вам, що\(x = -3\) це ________ стандартні відхилення до __________ (праворуч або ліворуч) середнього.

    Відповіді

    a Цей\(z\) -score говорить вам, що\(x = 10\) це 2.5 стандартні відхилення праворуч від середньої п'ятірки.

    б. припустимо випадкові\(Y\) величини\(X\) і мають такі нормальні розподіли:\(X \sim N(5, 6)\) і\(Y \sim N(2, 1)\). Якщо\(x = 17\), то\(z = 2\). (Це було показано раніше.) Якщо\(y = 4\), що таке\(z\)?

    \[z = \dfrac{y-\mu}{\sigma} = \dfrac{4-2}{1} = 2 \nonumber\]

    де\(\mu = 2\) і\(\sigma = 1\).

    \(z\)-оцінка для\(y = 4\) є\(z = 2\). Це означає, що чотири - це\(z = 2\) стандартні відхилення праворуч від середнього. Отже,\(x = 17\) і обидва\(y = 4\) є двома (своїми власними) стандартними відхиленнями праворуч від відповідних засобів.

    z -score дозволяє нам порівнювати дані, які масштабуються по-різному. Щоб зрозуміти концепцію, припустимо,\(X \sim N(5, 6)\) представляє збільшення ваги для однієї групи людей, які намагаються набрати вагу протягом шести тижнів і\(Y \sim N(2, 1)\) вимірює однаковий набір ваги для другої групи людей. Негативним збільшенням ваги буде втрата ваги. Оскільки\(x = 17\) і\(y = 4\) є кожними двома стандартними відхиленнями праворуч від своїх засобів, вони являють собою однаковий, стандартизований набір ваги щодо своїх засобів.

    Вправа\(\PageIndex{2}\)

    Заповніть заготовки.

    Джером в середньому 16 очок гри зі стандартним відхиленням в чотири очки. \(X \sim N(16, 4)\). Припустимо, Джером набирає десять очок у грі. \(z\)—score, коли\(x = 10\) є\(-1.5\). Цей бал говорить вам, що\(x = 10\) це _____ стандартні відхилення до ______ (праворуч або ліворуч) середнього______ (Що таке середнє?).

    Відповідь

    1.5, ліворуч, 16

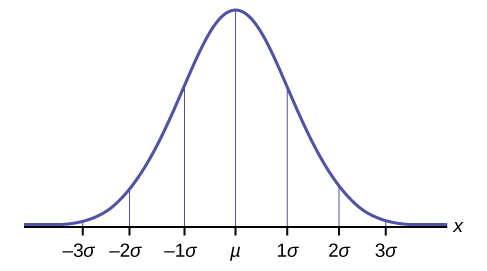
    Емпіричне правило

    Якщо\(X\) є випадковою величиною і має нормальний розподіл із\(\mu\) середнім і стандартним відхиленням\(\sigma\), то Емпіричне правило говорить наступне:

    • Близько 68%\(x\) значень лежать між —1\(\sigma\) і +1\(\sigma\) від середнього\(\mu\) (в межах одного стандартного відхилення від середнього).
    • Близько 95%\(x\) значень лежать між —2\(\sigma\) і +2\(\sigma\) від середнього\(\mu\) (в межах двох стандартних відхилень від середнього).
    • Близько 99,7%\(x\) значень лежать між —3\(\sigma\) і +3\(\sigma\) від середнього\(\mu\) (в межах трьох стандартних відхилень від середнього). Зверніть увагу, що практично всі\(x\) значення лежать в межах трьох стандартних відхилень від середнього.
    • \(z\)-бали для +1\(\sigma\) і —1\(\sigma\) складають +1 і —1 відповідно.
    • \(z\)-бали для +2\(\sigma\) і —2\(\sigma\) складають +2 і —2 відповідно.
    • \(z\)-бали для +3\(\sigma\) і -3\(\sigma\) складають +3 і —3 відповідно.

    Емпіричне правило також відоме як правило 68-95-99.7.

    альт
    Малюнок\(\PageIndex{1}\)

    Приклад\(\PageIndex{3}\)

    Середній зріст 15-18-річних самців з Чилі з 2009 по 2010 рік становив 170 см зі стандартним відхиленням 6,28 см. Чоловічі висоти, як відомо, дотримуються нормального розподілу. Нехай\(X =\) зріст 15-18-річного чоловіка з Чилі в 2009 по 2010 рік. Потім\(X \sim N(170, 6.28)\).

    1. Припустимо, що 15-18-річний чоловік з Чилі був 168 см у висоту з 2009 по 2010 рік. \(z\)-оцінка, коли\(x = 168\) см дорівнює\(z =\) _______. Цей\(z\) -оцінка говорить вам, що\(x = 168\) це ________ стандартні відхилення до ________ (праворуч або ліворуч) середнього _____ (Що таке середнє?).
    2. Припустимо, що зріст 15-18-річного чоловіка з Чилі з 2009 по 2010 рік має\(z\) -оцінка\(z = 1.27\). Який зріст самця? \(z\)-score (\(z = 1.27\)) говорить вам, що зріст самця становить ________ стандартні відхилення до __________ (праворуч або ліворуч) середнього.

    Відповіді

    1. —0.32, 0.32, лівий, 170
    2. 177.98, 1.27, праворуч

    Вправа\(\PageIndex{3}\)

    Використовуйте інформацію в прикладі,\(\PageIndex{3}\) щоб відповісти на наступні запитання.

    1. Припустимо, що 15-18-річний чоловік з Чилі був 176 см у висоту з 2009 по 2010 рік. \(z\)-оцінка, коли\(x = 176\) см дорівнює\(z =\) _______. Цей\(z\) -бал говорить вам, що\(x = 176\) см - це ________ стандартні відхилення до ________ (праворуч або ліворуч) середнього _____ (Що таке середнє?).
    2. Припустимо, що зріст 15-18-річного чоловіка з Чилі з 2009 по 2010 рік має\(z\) -оцінка\(z = –2\). Який зріст самця? \(z\)-score (\(z = –2\)) говорить вам, що зріст самця становить ________ стандартні відхилення до __________ (праворуч або ліворуч) середнього.
    Відповідь

    Розв'яжіть рівняння\(z = \dfrac{x-\mu}{\sigma}\) для\(z\). \(x = \mu+ (z)(\sigma)\)

    \(z = \dfrac{176-170}{6.28}\), Ця z -оцінка говорить вам, що\(x = 176\) см дорівнює 0,96 стандартних відхилень праворуч від середнього 170 см.

    Відповідь

    Розв'яжіть рівняння\(z = \dfrac{x-\mu}{\sigma}\) для\(z\). \(x = \mu+ (z)(\sigma)\)

    \(X = 157.44\)см, The\(z\) -score (\(z = –2\)) говорить про те, що зріст самця - це два стандартних відхилення зліва від середнього.

    Приклад\(\PageIndex{4}\)

    З 1984 по 1985 рік середній зріст 15-18-річних самців з Чилі становив 172,36 см, а стандартне відхилення - 6,34 см. Нехай зростання\(Y =\) від 15 до 18-річних самців з 1984 по 1985 рік. Потім\(Y \sim N(172.36, 6.34)\).

    Середній зріст 15-18-річних самців з Чилі з 2009 по 2010 рік становив 170 см зі стандартним відхиленням 6,28 см. Чоловічі висоти, як відомо, дотримуються нормального розподілу. Нехай\(X =\) зріст 15-18-річного чоловіка з Чилі в 2009 по 2010 рік. Потім\(X \sim N(170, 6.28)\).

    Знайдіть z -бали для\(x = 160.58\) см і\(y = 162.85\) см. Інтерпретувати кожен\(z\) -score. Що можна сказати про\(x = 160.58\) см і\(y = 162.85\) см?

    Відповідь

    • \(z\)-score (Рівняння\ ref {zscore}) для\(x = 160.58\) є\(z = –1.5\).
    • \(z\)-оцінка для\(y = 162.85\) є\(z = –1.5\).

    Обидва\(x = 160.58\) і\(y = 162.85\) відхиляються однакову кількість стандартних відхилень від відповідних засобів і в тому ж напрямку.

    Вправа\(\PageIndex{4}\)

    У 2012 році іспит SAT склали 1 664 479 студентів. Розподіл балів в словесному розділі САТ мало середнє\(\mu = 496\) і стандартне відхилення\(\sigma = 114\). Нехай\(X =\) SAT іспит словесний розділ оцінка в 2012 році. Потім\(X \sim N(496, 114)\).

    Знайти\(z\) -бали для\(x_{1} = 325\) і\(x_{2} = 366.21\). Інтерпретувати кожен\(z\) -score. Що можна сказати про\(x_{1} = 325\) і\(x_{2} = 366.21\)?

    Відповідь

    z -оцінка (рівняння\ ref {zscore}) для\(x_{1} = 325\) є\(z_{1} = –1.15\).

    z -оцінка (рівняння\ ref {zscore}) для\(x_{2} = 366.21\) є\(z_{2} = –1.14\).

    Студент 2 забив ближче до середнього, ніж Студент 1 і, так як вони обидва мали негативні\(z\) -бали, Студент 2 мав кращий бал.

    Приклад\(\PageIndex{5}\)

    Припустимо, х має нормальний розподіл із середнім значенням 50 і стандартним відхиленням 6.

    • Близько 68% значень х лежать в межах одного стандартного відхилення від середнього. Тому близько 68% значень х лежать між —1σ = (—1) (6) = —6 і 1σ = (1) (6) = 6 від середнього 50. Значення 50 - 6 = 44 і 50 + 6 = 56 знаходяться в межах одного стандартного відхилення від середнього 50. Z-бали складають —1 і +1 для 44 і 56 відповідно.
    • Близько 95% значень х лежать в межах двох стандартних відхилень від середнього. Тому близько 95% значень х лежать між —2σ = (—2) (6) = —12 і 2σ = (2) (6) = 12. Значення 50 - 12 = 38 і 50 + 12 = 62 знаходяться в межах двох стандартних відхилень від середнього 50. Z-бали складають —2 і +2 для 38 і 62 відповідно.
    • Близько 99,7% значень х лежать в межах трьох стандартних відхилень від середнього. Тому близько 99,7% значень х лежать між —3σ = (—3) (6) = —18 і 3σ = (3) (6) = 18 від середнього 50. Значення 50 - 18 = 32 і 50 + 18 = 68 знаходяться в межах трьох стандартних відхилень від середнього 50. Z-бали складають —3 і +3 для 32 і 68 відповідно.

    Вправа\(\PageIndex{5}\)

    Припустимо,\(X\) має нормальний розподіл із середнім значенням 25 і середнім відхиленням п'ять. Між якими значеннями\(x\) лежать 68% значень?

    Відповідь

    між 20 і 30.

    Приклад\(\PageIndex{6}\)

    З 1984 по 1985 рік середній зріст 15-18-річних самців з Чилі становив 172,36 см, а стандартне відхилення - 6,34 см. Нехай\(Y =\) зріст від 15 до 18-річних чоловіків в 1984 по 1985 рік. Потім\(Y \sim N(172.36, 6.34)\).

    1. Близько 68%\(y\) значень лежать між якими двома значеннями? Ці значення є ________________. \(z\)-бали є ________________ відповідно.
    2. Близько 95%\(y\) значень лежать між якими двома значеннями? Ці значення є ________________. \(z\)-бали є ________________ відповідно.
    3. Близько 99,7%\(y\) значень лежать між якими двома значеннями? Ці значення є ________________. \(z\)-бали є ________________ відповідно.

    Відповідь

    1. Близько 68% значень лежать між 166,02 і 178,7. \(z\)-бали становлять —1 і 1.
    2. Близько 95% значень лежать між 159,68 і 185,04. \(z\)-оцінки становлять —2 і 2.
    3. Близько 99,7% значень лежать між 153,34 і 191,38. \(z\)-оцінки становлять —3 і 3.

    Вправа\(\PageIndex{6}\)

    Бали на вступному іспиті до коледжу мають приблизний нормальний розподіл із середнім,\(\mu = 52\) балами та стандартним відхиленням,\(\sigma = 11\) балами.

    1. Близько 68%\(y\) значень лежать між якими двома значеннями? Ці значення є ________________. \(z\)-бали є ________________ відповідно.
    2. Близько 95%\(y\) значень лежать між якими двома значеннями? Ці значення є ________________. \(z\)-бали є ________________ відповідно.
    3. Близько 99,7%\(y\) значень лежать між якими двома значеннями? Ці значення є ________________. \(z\)-бали є ________________ відповідно.
    Відповідь на

    Близько 68% значень лежать між значеннями 41 і 63. \(z\)-бали складають —1 і 1 відповідно.

    Відповідь б

    Близько 95% значень лежить між значеннями 30 і 74. \(z\)-бали складають —2 і 2 відповідно.

    Відповідь c

    Близько 99,7% значень лежать між значеннями 19 і 85. \(z\)-бали складають —3 і 3 відповідно.

    Резюме

    A\(z\) -score - це стандартизоване значення. Його розподіл є стандартним нормальним,\(Z \sim N(0,1)\). The mean of the \(z\)-scores is zero and the standard deviation is one. If \(y\) is the z -score для значення\(x\) from the normal distribution \(N(\mu, \sigma)\) then \(z\) tells you how many standard deviations \(x\) is above (greater than) or below (less than) \(\mu\).

    Огляд формули

    \(Z \sim N(0, 1)\)

    \(z = a\)стандартизоване значення (\(z\)-оцінка)

    середнє = 0; стандартне відхилення = 1

    Щоб знайти\(K\) процентиль того,\(X\) коли відомі\(z\) -бали:

    \(k = \mu + (z)\sigma\)

    \(z\)-оцінка:\(z = \dfrac{x-\mu}{\sigma}\)

    \(Z =\)випадкова величина для z -scores

    \(Z \sim N(0, 1)\)

    Глосарій

    Стандартний нормальний розподіл
    неперервна випадкова величина (RV)\(X \sim N(0, 1)\); коли\(X\) слідує за стандартним нормальним розподілом, вона часто відзначається як\ (Z\ sim N (0, 1)\.
    \(z\)-оцінка
    лінійне перетворення форми\(z = \dfrac{x-\mu}{\sigma}\); якщо це перетворення застосовується до будь-якого нормального розподілу, результатом\(X \sim N(\mu, \sigma\) є стандартний нормальний розподіл\(Z \sim N(0,1)\). Якщо це перетворення застосовується до будь-якого конкретного\(x\) значення RV із середнім\(\mu\) і стандартним відхиленням\(\sigma\), результат називається\(z\) -score of\(x\). \(z\)-score дозволяє нам порівнювати дані, які зазвичай розподіляються, але масштабуються по-різному.

    Посилання

    1. «Артеріальний тиск чоловіків і жінок». Старт Крюч, 2013. Доступно в Інтернеті за адресою http://www.statcrunch.com/5.0/viewre...reportid=11960 (доступ до 14 травня 2013 р.).
    2. «Використання епідеміологічних інструментів у постраждалих від конфлікту населення: освітні ресурси з відкритим доступом для політиків: розрахунок z-балів». Лондонська школа гігієни та тропічної медицини, 2009. Доступно в Інтернеті за адресою http://conflict.lshtm.ac.uk/page_125.htm (доступ до 14 травня 2013 р.).
    3. «2012 Коледж Bound старших людей загального профілю групи звіт.» Коледжська рада, 2012. Доступно в Інтернеті за адресою media.collegeboard.com/digita... Group-2012.pdf (доступ до 14 травня 2013).
    4. «Дайджест статистики освіти: ACT оцінка середній і стандартні відхилення за статтю і расовий/етнічної приналежності і відсоток учасників тестування ACT, за вибраними складовими діапазонами балів і запланованих областях дослідження: Вибрані роки, 1995 по 2009». Національний центр статистики освіти. Доступний в Інтернеті за адресою nces.ed.gov/програми/дайджест/д... s/dt09_147.asp (доступ до 14 травня 2013).
    5. Дані з San Jose Mercury News.
    6. Дані Всесвітнього альманаху та Книги фактів.
    7. «Список стадіонів по місткості». Вікіпедія. Доступно в Інтернеті за адресою uk.wikipedia.org/wiki/list_o... ms_by_capacity (доступ до 14 травня 2013 р.).
    8. Дані Національної баскетбольної асоціації. Доступно в Інтернеті за адресою www.nba.com (доступ до 14 травня 2013 р.).