5.1: Вступ

Last updated
Save as PDF

Page ID: 98473

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

ЦІЛІ ГЛАВИ

До кінця цієї глави учень повинен вміти:

Розпізнавати та розуміти безперервні функції щільності ймовірностей загалом.
Розпізнайте рівномірний розподіл ймовірностей і застосуйте його належним чином.
Розпізнайте експоненціальний розподіл ймовірностей та застосуйте його належним чином.

Безперервні випадкові величини мають безліч застосувань. Бейсбол ватин середні, IQ бали, тривалість часу тривалості міжміського телефонного дзвінка, кількість грошей, яку людина несе, тривалість часу триває комп'ютерний чіп, і бали SAT лише кілька. Поле надійності залежить від безлічі неперервних випадкових величин.

Значення дискретних і неперервних випадкових величин можуть бути неоднозначними. Наприклад, якщо\(X\) дорівнює кількості миль (до найближчої милі), яку ви їдете на роботу, то\(X\) це дискретна випадкова величина. Ви вважаєте милі. Якщо\(X\) відстань, яку ви їдете на роботу, то ви вимірюєте значення\(X\) і\(X\) є безперервною випадковою величиною. Для другого прикладу, якщо\(X\) дорівнює кількості книг в рюкзаку, то\(X\) це дискретна випадкова величина. Якщо\(X\) вага книги, то\(X\) це безперервна випадкова величина, оскільки вимірюються ваги. Як визначається випадкова величина, дуже важливо.

На зображенні зображені рослини редьки різної висоти, що проростають з бруду. — Малюнок\(\PageIndex{1}\): Висоти цих рослин редьки є безперервними випадковими величинами. (Кредит: Rev Стен)

Властивості неперервних розподілів ймовірностей

Графік безперервного розподілу ймовірностей є кривою. Імовірність представлена площею під кривою. Крива називається функцією щільності ймовірності (скорочено pdf). Ми використовуємо символ\(f(x)\) для представлення кривої. \(f(x)\)функція, яка відповідає графіку; ми використовуємо функцію щільності\(f(x)\) для малювання графіка розподілу ймовірностей. Площа під кривою задається іншою функцією, яка називається функцією кумулятивного розподілу (скорочено cdf). Функція кумулятивного розподілу використовується для оцінки ймовірності як площі.

Результати вимірюються, а не зараховуються.
Вся площа під кривою і над віссю х дорівнює одиниці.
Ймовірність виявляється для інтервалів\(x\) значень, а не для окремих\(x\) значень.
\(P(c < x < d)\)- ймовірність того, що випадкова величина\(X\) знаходиться в проміжку між значеннями\(c\) і\(d\). \(P(c < x < d)\)область під кривою, над віссю x, праворуч\(c\) і ліворуч від\(d\).
\(P(x = c) = 0\)Імовірність того, що\(x\) приймає будь-яке єдине індивідуальне значення, дорівнює нулю. Площа нижче кривої, вище осі х, і між\(x = c\) і не\(x = c\) має ширини, а отже, немає площі (площа = 0). Так як ймовірність дорівнює площі, ймовірність також дорівнює нулю.
\(P(c < x < d)\)така ж, як і\(P(c \leq x \leq d)\) тому, що ймовірність дорівнює площі.

Ми знайдемо площу, яка представляє ймовірність, використовуючи геометрію, формули, технологію або таблиці ймовірностей. Загалом, обчислення потрібне для пошуку площі під кривою для багатьох функцій щільності ймовірностей. Коли ми використовуємо формули для пошуку площі в цьому підручнику, формули були знайдені за допомогою методів інтегрального числення. Однак, оскільки більшість студентів, які беруть цей курс, не вивчали обчислення, ми не будемо використовувати обчислення в цьому підручнику. Існує багато безперервних розподілів ймовірностей. При використанні безперервного розподілу ймовірностей для моделювання ймовірності використовується розподіл вибирається для моделювання та найкращого відповідності конкретній ситуації.

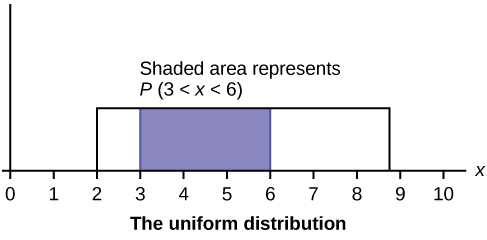
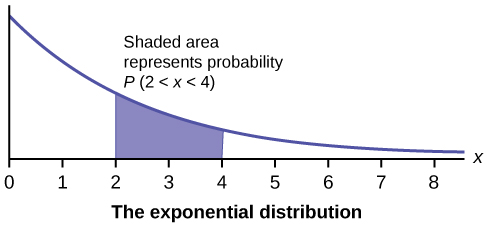
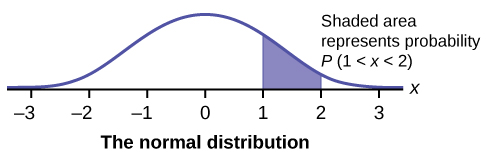
У цьому розділі та наступному ми вивчимо рівномірний розподіл, експоненціальний розподіл та нормальний розподіл. Наступні графіки ілюструють ці дистрибутиви.

Рисунок\(\PageIndex{2}\): На графіку показано рівномірний розподіл з областю між\(x = 3\) і\(x = 6\) затіненою для представлення ймовірності того, що значення випадкової величини\(X\) знаходиться в інтервалі між трьома і шістьма.

Рисунок\(\PageIndex{3}\): Графік показує експоненціальний розподіл з областю між\(x = 2\) і\(x = 4\) затіненою для представлення ймовірності того, що значення випадкової величини\(X\) знаходиться в інтервалі між двома і чотирма.

Рисунок\(\PageIndex{4}\): На графіку показано стандартний нормальний розподіл з областю між\(x = 1\) і\(x = 2\) затіненою для представлення ймовірності того, що значення випадкової величини\(X\) знаходиться в інтервалі між одиницею і двома.

Глосарій

Рівномірний розподіл: безперервна випадкова величина (RV), яка має однаково ймовірні результати над доменом\(a < x < b\); її часто називають прямокутним розподілом, оскільки графік PDF має форму прямокутника. Позначення:\(X \sim U(a,b)\). Середнє значення є\(\mu = \frac{a+b}{2}\) і стандартне відхилення є\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\). Функція щільності ймовірності -\(f(x) = \frac{1}{b-a}\) for\(a < x < b\) or\(a \leq x \leq b\). Сукупний розподіл є\(P(X \leq x) = \frac{x-a}{b-a}\).

Експоненціальний розподіл: безперервна випадкова величина (RV), яка з'являється, коли ми зацікавлені в інтервалах часу між деякими випадковими подіями, наприклад, тривалість часу між надзвичайними прибуття в лікарню; позначення є\(X \sim \text{Exp}(m)\). Середнє значення є\(\mu = \frac{1}{m}\) і стандартне відхилення є\(\sigma = \frac{1}{m}\). Функція щільності ймовірності є\(f(x) = me^{-mx}\),\(x \geq 0\) а функція кумулятивного розподілу -\(P(X \leq x) = 1 − e^{mx}\).