5.3: Рівномірний розподіл

Рівномірний розподіл є безперервним розподілом ймовірностей і стосується подій, які однаково ймовірні. При розробці проблем, які мають рівномірний розподіл, будьте уважні, чи є дані інклюзивними або виключними.

Приклад 5.3.1

Дані в таблиці\(\PageIndex{1}\) - це 55 усміхнених разів, у секундах, восьмитижневої дитини.

Таблиця\(\PageIndex{1}\)

10.4	19.6	18.8	13,9	17.8	16.8	21.6	17,9	12.5	11.1	4.9
12.8	14.8	22.8	20.0	15,9	16.3	13,4	17.1	14.5	19,0	22.8
1.3	0.7	8.9	11.9	10.9	7.3	5.9	3.7	17,9	19.2	9.8
5.8	6.9	2.6	5.8	21.7	11.8	3.4	2.1	4.5	6.3	10.7
8.9	9.4	9.4	7.6	10.0	3.3	6.7	7.8	11.6	13,8	18.6

Середнє значення зразка = 11,49 і стандартне відхилення зразка = 6,23.

Будемо вважати, що усміхнені часи, в секундах, слідують рівномірному розподілу між нулем і 23 секундами включно. Це означає, що будь-який час посмішки від нуля до 23 секунд включно однаково вірогідний. Гістограма, яка може бути побудована з зразка, є емпіричним розподілом, який тісно відповідає теоретичному рівномірному розподілу.

Нехай\(X =\) довжина, в секундах, восьмитижневої посмішки дитини.

Позначення для рівномірного розподілу

\(X \sim U(a, b)\)де\(a =\) найнижче значення\(x\)\(b =\) і найбільше значення\(x\).

Функція щільності ймовірності призначена\(f(x) = \frac{1}{b-a}\) для\(a \leq x \leq b\).

Для цього прикладу\(X \sim U(0, 23)\) і\(f(x) = \frac{1}{23-0}\) для\(0 \leq X \leq 23\).

Формули теоретичного середнього і стандартного відхилення

\[\mu = \frac{a+b}{2} \nonumber\]

і

\[\sigma = \sqrt{\frac{(b-a)^{2}}{12}} \nonumber\]

Для цієї задачі теоретичне середнє і стандартне відхилення

\[\mu = \frac{0+23}{2} = 11.50 \, seconds \nonumber\]

і

\[\sigma = \frac{(23-0)^{2}}{12} = 6.64\, seconds. \nonumber\]

Зверніть увагу, що теоретичне середнє і стандартне відхилення близькі до вибіркового середнього та стандартного відхилення в цьому прикладі.

Вправа\(\PageIndex{1}\)

Дані, які слідують, є кількість пасажирів на 35 різних чартерних рибальських човнів. Середнє значення зразка = 7,9, а стандартне відхилення вибірки = 4,33. Дані слідують за рівномірним розподілом, де всі значення між нулем і 14 включно однаково вірогідні. Створіть значення a і\(b\). Запишіть розподіл в належних позначеннях, і обчисліть теоретичне середнє і стандартне відхилення.

Таблиця\(\PageIndex{2}\)

1	12	4	10	4	14	11
7	11	4	13	2	4	6
3	10	0	12	6	9	10
5	13	4	10	14	12	11
6	10	11	0	11	13	2

Відповідь

\(a\)нуль;\(b\) є;\(14\);\(\mu = 7\) пасажири\(X \sim U (0, 14)\);\(\sigma = 4.04\) пасажири

Приклад 5.3.2A

a Див. приклад 5.3.1. Яка ймовірність того, що випадково обрана восьмитижнева дитина посміхається від двох до 18 секунд?

Відповідь

а. знайти\(P(2 < x < 18)\).

\(P(2 < x < 18) = (\text{base})(\text{height}) = (18 – 2)\left(\frac{1}{23}\right) = \left(\frac{16}{23}\right)\).

Малюнок\(\PageIndex{1}\)

Вправа\(\PageIndex{2}\)B

b. знайти ^90-й процентиль для восьмитижневого часу посмішки дитини.

Відповідь

б Дев'яносто відсотків усміхнених часів падають нижче ^90-го процентиля\(k\), так\(P(x < k) = 0.90\)

\[P(x < k)= 0.90\]

\[(\text{base})(\text{height}) = 0.90\]

\[(k−0)\left(\frac{1}{23}\right) = 0.90\]

\[k = (23)(0.90) = 20.7\]

Малюнок\(\PageIndex{2}\)

Вправа\(\PageIndex{3}\)C

c Знайдіть ймовірність того, що випадкова восьмитижнева дитина посміхається більше 12 секунд ЗНАЮЧИ, що дитина посміхається БІЛЬШЕ ВОСЬМИ СЕКУНД.

Відповідь

c. це питання ймовірності є умовним. Вас просять знайти ймовірність того, що восьмитижнева дитина посміхається більше 12 секунд, коли ви вже знаєте, що дитина посміхається більше восьми секунд.

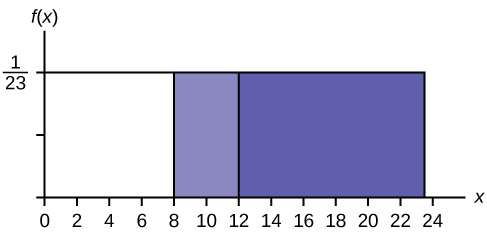
Знайти\(P(x > 12 | x > 8)\) Існує два способи вирішити проблему. Для першого способу використовуйте той факт, що це умовний і змінює простір вибірки. Графік ілюструє новий простір вибірки. Ви вже знаєте, що малюк посміхнувся більше восьми секунд.

Напишіть новий\(f(x): f(x) = \frac{1}{23-8} = \frac{1}{15}\)

для\(8 < x < 23\)

\(P(x > 12 | x > 8) = (23 − 12)\left(\frac{1}{15}\right) = \left(\frac{11}{15}\right)\)

Малюнок\(\PageIndex{3}\)

Для другого способу використовуйте умовну формулу з ймовірності теми з вихідним розподілом\(X \sim U(0, 23)\):

\(P(\text{A|B}) = \frac{P(\text{A AND B})}{P(\text{B})}\)

Для цієї проблеми\(\text{A}\) є (\(x > 12\)) і\(\text{B}\) is (\(x > 8\)).

Отже,\(P(x > 12|x > 8) = \frac{(x > 12 \text{ AND } x > 8)}{P(x > 8)} = \frac{P(x > 12)}{P(x > 8)} = \frac{\frac{11}{23}}{\frac{15}{23}} = \frac{11}{15}\)

Малюнок\(\PageIndex{4}\): Темніша затінена область представляє\(P(x > 12)\). Показує вся затінена область\(P(x > 8)\).

Вправа\(\PageIndex{2}\)

Розподіл дається як\(X \sim U(0, 20)\). Що таке\(P(2 < x < 18)\)? Знайдіть ^90-й процентиль.

Відповідь

\(P(2 < x < 18) = 0.8\); ^90-й процентиль\(= 18\)

Приклад 5.3.3

Кількість часу, в хвилинах, яке людина повинна чекати автобуса, рівномірно розподіляється між нулем і 15 хвилинами включно.

Вправа\(\PageIndex{3}\).1

а. яка ймовірність того, що людина чекає менше 12,5 хвилин?

Відповідь

а. нехай\(X =\) кількість хвилин людина повинна чекати автобуса. \(a = 0\)і\(b = 15\). \(X \sim U(0, 15)\). Запишіть функцію щільності ймовірності. \(f(x) = \frac{1}{15-0} = \frac{1}{15}\)для\(0 \leq x \leq 15\).

Знайти\(P(x < 12.5)\). Намалюйте графік.

\[P(x < k) = (\text{base})(\text{height}) = (12.5−0)\left(\frac{1}{15}\right) = 0.8333\]

Імовірність того, що людина чекає менше 12,5 хвилин, становить 0,8333.

Малюнок\(\PageIndex{5}\).

Вправа\(\PageIndex{3}\).2

б. в середньому, скільки часу повинен чекати людина? Знайти середнє\(\mu\), і стандартне відхилення,\(\sigma\).

Відповідь

б\(\mu = \frac{a+b}{2} = \frac{15+0}{2} = 7.5\). В середньому людина повинна почекати 7,5 хвилин.

\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}} = \sqrt{\frac{(12-0)^{2}}{12}} = 4.3\). Стандартне відхилення становить 4,3 хвилини.

Вправа\(\PageIndex{3}\).3

c Дев'яносто відсотків часу, час, який людина повинна чекати, падає нижче якого значення?

Примітка 5.3.3.3.1

Це просить ^90-й процентиль.

Відповідь

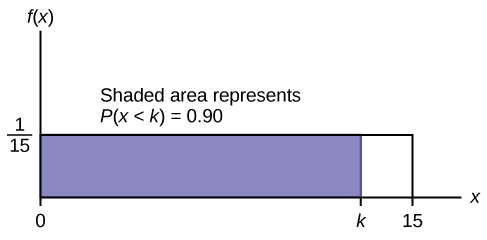
c. знайти ^90-й процентиль. Намалюйте графік. Нехай\(k =\) ^90-й процентиль.

\(P(x < k) = (\text{base})(\text{height}) = (k−0)\left(\frac{1}{15}\right)\)
\(0.90 = (k)\left(\frac{1}{15}\right)\)
\(k = (0.90)(15) = 13.5\)
\(k\)іноді називають критичним значенням.
^90-й процентиль становить 13,5 хвилин. Дев'яносто відсотків часу людина повинна чекати не більше 13,5 хвилин.

Малюнок\(\PageIndex{6}\).

Вправа\(\PageIndex{4}\)

Загальна тривалість бейсбольних ігор у вищій лізі в сезоні 2011 рівномірно розподілена між 447 годин і 521 годин включно.

1. Знайдіть\(a\)\(b\) і опишіть, що вони собою представляють.
2. Напишіть дистрибутив.
3. Знайдіть середнє і стандартне відхилення.
4. Яка ймовірність того, що тривалість ігор для команди в сезоні 2011 року становить від 480 до 500 годин?
5. Який ^65-й процентиль за тривалістю ігор за команду за сезон 2011 року?

Відповідь

1. \(a\)є\(447\), і\(b\) є\(521\). a - мінімальна тривалість ігор для команди в сезоні 2011, і\(b\) максимальна тривалість ігор для команди в сезоні 2011 року.
2. \(X \sim U(447, 521)\).
3. \(\mu = 484\), і\(\sigma = 21.36\)

   

   Малюнок\(\PageIndex{1}\).

4. \(P(480 < x < 500) = 0.2703\)
5. ^65-й процентиль становить 495,1 години.

Приклад 5.3.4

Припустимо, час, який потрібен дев'ятирічному віку, щоб з'їсти пончик, становить від 0,5 до 4 хвилин включно. Нехай\(X =\) час, в хвилинах, потрібно дев'ятирічній дитині з'їсти пончик. Потім\(X \sim U(0.5, 4)\).

а. ймовірність того, що випадково обраний дев'ятирічна дитина з'їсть пончик не менше ніж за дві хвилини, становить _______.

Рішення

а. 0,5714

Вправа\(\PageIndex{4}\).1

б. знайти ймовірність того, що інший дев'ятирічна дитина з'їсть пончик більше ніж за дві хвилини з огляду на те, що дитина вже їсть пончик більше 1,5 хвилин.

Друге питання має умовну ймовірність. Вас просять знайти ймовірність того, що дев'ятирічна дитина з'їсть пончик більше ніж за дві хвилини з огляду на те, що дитина вже їсть пончик більше 1,5 хвилин. Вирішити проблему можна двома різними способами (див. Приклад). Необхідно зменшити простір зразка. Перший спосіб: Оскільки ви знаєте, що дитина вже їсть пончик більше 1,5 хвилин, ви вже не починаєте з = 0,5 хвилини. Ваша відправна точка - 1,5 хвилини.

Напишіть нове\(f(x)\):

\(f(x) = \frac{1}{4-1.5} = \frac{2}{5}\)для\(1.5 \leq x \leq 4\).

Знайти\(P(x > 2|x > 1.5)\). Намалюйте графік.

Малюнок\(\PageIndex{2}\).

\(P(x > 2|x > 1.5) = (\text{base})(\text{new height}) = (4 − 2)(25)\left(\frac{2}{5}\right) =\)?

Відповідь

б.\(\frac{4}{5}\)

Імовірність того, що дев'ятирічна дитина з'їсть пончик більше ніж за дві хвилини з урахуванням того, що дитина вже їсть пончик більше 1,5 хвилин, є\(\frac{4}{5}\).

Другий спосіб: Намалюйте початковий графік для\(X \sim U(0.5, 4)\). Використовуйте умовну формулу

\(P(x > 2 | x > 1.5) = \frac{P(x > 2 \text{AND} x > 1.5)}{P(x > 1.5)} = \frac{P(x>2)}{P(x>1.5)} = \frac{\frac{2}{3.5}}{\frac{2.5}{3.5}} = 0.8 = \frac{4}{5}\)

Вправа\(\PageIndex{5}\)

Припустимо, час, необхідний студенту, щоб закінчити вікторину, рівномірно розподіляється між шістьма і 15 хвилинами включно. Нехай\(X =\) час, у хвилинах, це займе студент, щоб закінчити вікторину. Потім\(X \sim U(6, 15)\).

Знайдіть ймовірність того, що випадково обраному студенту потрібно щонайменше вісім хвилин, щоб пройти тест. Потім знайдіть ймовірність того, що іншому студенту потрібно щонайменше вісім хвилин, щоб закінчити вікторину, враховуючи, що вона вже зайняла більше семи хвилин.

Відповідь

\(P(x > 8) = 0.7778\)

\(P(x > 8 | x > 7) = 0.875\)

Приклад 5.3.5

Служба опалення та кондиціонування повітря Ace виявляє, що кількість часу, необхідного ремонтнику для фіксації печі, рівномірно розподіляється між 1,5 та чотирма годинами. Нехай\(x =\) час, необхідний для фіксації печі. Потім\(x \sim U(1.5, 4)\).

1. Знайдіть ймовірність того, що випадково обраний ремонт печі вимагає більше двох годин.
2. Знайдіть ймовірність того, що випадково обраний ремонт печі вимагає менше трьох годин.
3. Знайдіть ^30-й процентиль часу ремонту печі.
4. Найдовші 25% часу ремонту печі займають принаймні скільки часу? (Іншими словами: знайти мінімальний час для найдовших 25% часу ремонту.) Що це за процентиль?
5. Знайти середнє і стандартне відхилення

Рішення

а. знайти\(f(x): f(x) = \frac{1}{4-1.5} = \frac{1}{2.5}\) так\(f(x) = 0.4\)

\(P(x > 2) = (\text{base})(\text{height}) = (4 – 2)(0.4) = 0.8\)

Малюнок\(\PageIndex{3}\). Рівномірний розподіл між 1,5 і чотирма із затіненою областю між двома та чотирма, що представляє ймовірність того,\(x\) що час ремонту більше двох

б.\(P(x < 3) = (\text{base})(\text{height}) = (3 – 1.5)(0.4) = 0.6\)

Графік прямокутника, що показує весь розподіл, залишиться колишнім. Однак графік повинен бути затінений між\(x = 1.5\) і\(x = 3\). Зверніть увагу, що затінена область починається з,\(x = 1.5\) а не на\(x = 0\); оскільки\(X \sim U(1.5, 4)\), не\(x\) може бути менше 1,5.

Малюнок\(\PageIndex{4}\). Рівномірний розподіл між 1,5 і чотирма із затіненою площею від 1,5 до трьох, що представляє ймовірність того,\(x\) що час ремонту менше трьох

c.

Малюнок\(\PageIndex{5}\). Рівномірний розподіл між 1,5 і 4 з площею 0,30, затіненою вліво, що становить найкоротші 30% часу ремонту.

\(P(x < k) = 0.30\)
\(P(x < k) = (\text{base})(\text{height}) = (k – 1.5)(0.4)\)
\(0.3 = (k – 1.5) (0.4)\); Вирішити знайти\(k\):
\(0.75 = k – 1.5\), отримані діленням обох сторін на 0,4
\(k = 2.25\), отриманого додаванням 1,5 до обох сторін

^30-й процентиль часу ремонту становить 2,25 години. 30% часу ремонту становить 2,25 години або менше.

д.

Малюнок\(\PageIndex{6}\). Рівномірний розподіл між 1,5 і 4 з площею 0,25 затіненої праворуч, що становить найдовший 25% часу ремонту.

\(P(x > k) = 0.25\)
\(P(x > k) = (\text{base})(\text{height}) = (4 – k)(0.4)\)
\(0.25 = (4 – k)(0.4)\); Вирішити для\(k\):
\(0.625 = 4 − k\),
отриманого діленням обох сторін на 0,4
\(−3.375 = −k\),
отриманого відніманням чотирьох з обох сторін: \(k = 3.375\)
Найдовші 25% ремонту печі займають не менше 3,375 годин (3,375 годин або довше).

Примітка: Оскільки 25% часу ремонту становить 3.375 годин або більше, це означає, що 75% часу ремонту становить 3.375 годин або менше. 3.375 годин - це ^75-й процентиль часу ремонту печі.

е.\(\mu = \frac{a+b}{2}\) і\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\)

\(\mu = \frac{1.5+4}{2} = 2.75\)годин і\(\sigma = \sqrt{\frac{(4-1.5)^{2}}{12}} = 0.7217\) годин

Вправа\(\PageIndex{6}\)

Кількість часу, необхідного сервісному майстру для заміни масла в автомобілі, рівномірно розподіляється між 11 і 21 хвилиною. Нехай\(X =\) час, необхідний для заміни масла на автомобілі.

1. Запишіть випадкову величину\(X\) в словах. \(X =\)__________________.
2. Напишіть дистрибутив.
3. Графік розподілу.
4. Знайти\(P(x > 19)\).
5. Знайдіть ^50-й процентиль.

Відповідь

1. Нехай\(X =\) час, необхідний для заміни масла в автомобілі.
2. \(X \sim U(11, 21)\).

3. 

   Малюнок\(\PageIndex{7}\).

4. \(P(x > 19) = 0.2\)
5. ^50-й процентиль становить 16 хвилин.

Рецензія

Якщо\(X\) має рівномірний розподіл де\(a < x < b\) або\(a \leq x \leq b\), то\(X\) приймає значення між\(a\) і\(b\) (може включати\(a\) і\(b\)). Всі значення\(x\) однаково вірогідні. Пишемо\(X \sim U(a, b)\). Середнє значення\(X\) є\(\mu = \frac{a+b}{2}\). Стандартне відхилення\(X\) є\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\). Функція щільності ймовірності\(X\) is\(f(x) = \frac{1}{b-a}\) for\(a \leq x \leq b\). Сукупна функція розподілу\(X\) is\(P(X \leq x) = \frac{x-a}{b-a}\). \(X\)є безперервним.

Малюнок\(\PageIndex{8}\).

Імовірність\(P(c < X < d)\) може бути знайдена шляхом обчислення площі під\(f(x)\), між\(c\) і\(d\). Оскільки відповідна область є прямокутником, площа може бути знайдена простим множенням ширини і висоти.

Огляд формули

\(X =\)дійсне число між\(a\) і\(b\) (в деяких випадках\(X\) може приймати значення\(a\) і\(b\)). \(a =\)найменший\(X\);\(b =\) найбільший\(X\)

\(X \sim U(a, b)\)

Середнє значення є\(\mu = \frac{a+b}{2}\)

Стандартне відхилення становить\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\)

Функція щільності ймовірності:\(f(x) = \frac{1}{b-a} \text{for} a \leq X \leq b\)

Зона ліворуч від\(x\):\(P(X < x) = (x – a)\left(\frac{1}{b-a}\right)\)

Площа праворуч від\(x\): P (\(X\)>\(x\)) = (b — x)\(\left(\frac{1}{b-a}\right)\)

Площа між\(c\) і\(d\):\(P(c < x < d) = (\text{base})(\text{height}) = (d – c)\left(\frac{1}{b-a}\right)\)

Уніформа:\(X \sim U(a, b)\) де\(a < x < b\)

• pdf:\(f(x) = \frac{1}{b-a}\) для\(a \leq x \leq b\)
• CDF:\(P(X \leq x) = \frac{x-a}{b-a}\)
• означає\(\mu = \frac{a+b}{2}\)
• стандартне відхилення\(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\)
• \(P(c < X < d) = (d – c)\left(\frac{1}{b-a}\right)\)

Посилання

Макдугалл, Джон А. Програма Макдугалла для максимальної втрати ваги. Шлейф, 1995.

Використовуйте наступну інформацію, щоб відповісти на наступні десять питань. Дані, які слідують, - це квадратні метри (у квадраті 1000 футів) 28 будинків.

1.5	2.4	3.6	2.6	1.6	2.4	2.0
3.5	2.5	1.8	2.4	2.5	3.5	4.0
2.6	1.6	2.2	1.8	3.8	2.5	1.5
2.8	1.8	4.5	1.9	1.9	3.1	1.6

Середнє значення зразка = 2,50 і стандартне відхилення зразка = 0,8302.

Дистрибутив можна записати як\(X \sim U(1.5, 4.5)\).

Вправа\(\PageIndex{7}\)

Що це за тип дистрибуції?

Вправа\(\PageIndex{8}\)

У цьому розподілі результати однаково вірогідні. Що це означає?

Відповідь

Це означає, що значення х так само, як імовірно, буде будь-яке число між 1.5 і 4.5.

Вправа\(\PageIndex{9}\)

Яка висота\(f(x)\) для безперервного розподілу ймовірностей?

Вправа\(\PageIndex{10}\)

Які обмеження для значень\(x\)?

Відповідь

\(1.5 \leq x \leq 4.5\)

Вправа\(\PageIndex{11}\)

Графік\(P(2 < x < 3)\).

Вправа\(\PageIndex{12}\)

Що таке\(P(2 < x < 3)\)?

Відповідь

0,333

Вправа\(\PageIndex{13}\)

Що таке\(P(x < 3.5 | x < 4)\)?

Вправа\(\PageIndex{14}\)

Що таке\(P(x = 1.5)\)?

Відповідь

нуль

Вправа\(\PageIndex{15}\)

Що таке ^90-й процентиль квадратних метрів для будинків?

Вправа\(\PageIndex{16}\)

Знайдіть ймовірність того, що випадково обраний будинок має більше 3,000 квадратних футів, враховуючи, що ви вже знаєте, що будинок має більше 2,000 квадратних футів.

Відповідь

0.6

Вправа\(\PageIndex{17}\)

Що таке\(a\)? Що вона собою являє?

Вправа\(\PageIndex{18}\)

Що таке\(b\)? Що вона собою являє?

Відповідь

\(b\)є\(12\), і вона являє собою найвищу цінність\(x\).

Вправа\(\PageIndex{19}\)

Що таке функція щільності ймовірності?

Вправа\(\PageIndex{20}\)

Що таке теоретичне означає?

Відповідь

шість

Вправа\(\PageIndex{21}\)

Що таке теоретичне стандартне відхилення?

Вправа\(\PageIndex{22}\)

Намалюйте графік розподілу для\(P(x > 9)\).

Відповідь

Малюнок\(\PageIndex{9}\).

Вправа\(\PageIndex{23}\)

Знайти\(P(x > 9)\).

Вправа\(\PageIndex{24}\)

Знайдіть ^40-й процентиль.

Відповідь

4.8

Використовуйте наступну інформацію, щоб відповісти на наступні одинадцять вправ. Вік автомобілів на стоянці персоналу заміського коледжу рівномірно розподіляється від півроку (0,5 року) до 9,5 років.

Вправа\(\PageIndex{25}\)

Що тут вимірюється?

Вправа\(\PageIndex{26}\)

У словах визначаємо випадкову величину\(X\).

Відповідь

\(X\)= Вік (в роках) автомобілів на стоянці персоналу

Вправа\(\PageIndex{27}\)

Дані дискретні або безперервні?

Вправа\(\PageIndex{28}\)

Інтервал значень для\(x\) - ______.

Відповідь

Від 0,5 до 9,5

Вправа\(\PageIndex{29}\)

Розподіл\(X\) для ______.

Вправа\(\PageIndex{30}\)

Запишіть функцію щільності ймовірності.

Відповідь

\(f(x) = \frac{1}{9}\)де\(x\) знаходиться від 0,5 до 9,5 включно.

Вправа\(\PageIndex{31}\)

Графік розподілу ймовірностей.

1. Намалюйте графік розподілу ймовірностей.

   

   Малюнок\(\PageIndex{10}\).

2. Визначте наступні значення:
   1. Найнижче значення для\(\bar{x}\): _______
   2. Найвище значення для\(\bar{x}\): _______
   3. Висота прямокутника: _______
   4. Мітка для осі x (слова): _______
   5. Мітка для осі y (слова): _______

Вправа\(\PageIndex{32}\)

Знайдіть середній вік автомобілів в партії.

Відповідь

\(\mu\)= 5

Вправа\(\PageIndex{33}\)

Знайдіть ймовірність того, що випадково обраному автомобілю в партії було менше чотирьох років.

1. Намалюйте графік і затіньте цікаву область.

   

   Малюнок\(\PageIndex{11}\).

2. Знайдіть ймовірність. \(P(x < 4) =\)_______

Вправа\(\PageIndex{34}\)

Розглядаючи тільки автомобілі менше 7,5 років, знайдіть ймовірність того, що випадково обраному автомобілю в партії було менше чотирьох років.

1. Намалюйте графік, затіньте цікаву область.

   

   Малюнок\(\PageIndex{12}\).

2. Знайдіть ймовірність. \(P(x < 4 | x < 7.5) =\)_______

Відповідь

1. Перевірте рішення студента.
2. \(\frac{3.5}{7}\)

Вправа\(\PageIndex{35}\)

Що змінилося в попередніх двох проблемах, що зробило рішення різними

Вправа\(\PageIndex{36}\)

Знайдіть третій квартиль вікових автомобілів в партії. Це означає, що вам доведеться знайти значення таке\(\frac{3}{4}\), що або 75% автомобілів є максимум (менше або дорівнює) цього віку.

1. Намалюйте графік і затіньте цікаву область.

   

   Малюнок\(\PageIndex{13}\).

2. Знайдіть значення\(k\) таке, що\(P(x < k) = 0.75\).
3. Третій квартиль - _______

Відповідь

1. Перевірте рішення студента.
2. \(k = 7.25\)
3. \(7.25\)

Глосарій

Умовна ймовірність

ймовірність того, що подія відбудеться з огляду на те, що інша подія вже сталася