4.6: Гіпергеометричний розподіл

Last updated
Save as PDF

Page ID: 98302

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Гіпергеометричний розподіл виникає, коли одна вибірка з кінцевої популяції, що робить випробування залежними один від одного. Існує п'ять характеристик гіпергеометричного експерименту.

Характеристика гіпергеометричного експерименту

Ви берете проби з двох груп.
Вас турбує група за інтересами, яка називається першою групою.
Ви вибірку без заміни з комбінованих груп. Наприклад, ви хочете вибрати софтбольну команду з об'єднаної групи з 11 чоловіків і 13 жінок. Команда складається з десяти гравців.
Кожен підбір не є самостійним, так як відбір проб проводиться без заміни. У прикладі софтболу ймовірність вибрати жінку в першу чергу є\(\frac{13}{24}\). Імовірність вибору чоловіка другого є в тому\(\frac{11}{23}\) випадку, якщо жінка була підібрана першою. Це\(\frac{10}{23}\) якщо чоловік був обраний першим. Імовірність другого вибору залежить від того, що сталося в першому пікіровці.
Ви не маєте справу з випробуваннями Бернуллі.

Результати гіпергеометричного експерименту відповідають гіпергеометричному розподілу ймовірностей. Випадкова величина\(X\) = кількість елементів з групи, що цікавить.

Приклад\(\PageIndex{1}\)

Блюдо для цукерок містить 100 драже і 80 желейних крапель. П'ятдесят цукерок вибираються навмання. Яка ймовірність того, що 35 з 50 - це камеді? Дві групи - драже і камеді. Оскільки питання ймовірності запитує ймовірність підхоплення жувальних крапель, група інтересів (перша група) - це gumdrops. Розмір групи, що цікавить (перша група) - 80. Розмір другої групи - 100. Розмір проби - 50 (драже або мармелад). Нехай\(X =\) кількість крапель ясна в пробі 50. \(X\)приймає на себе значення\(x = 0, 1, 2, ..., 50\). Що таке твердження ймовірності написано математично?

Відповідь

\(P(x = 35)\)

Вправа\(\PageIndex{1}\)

Мішок містить літерні плитки. Сорок чотири плитки - голосні, а 56 - приголосні. Сім плиток вибираються випадковим чином. Ви хочете знати ймовірність того, що чотири з семи плиток є голосними. Що таке група інтересів, розмір групи, що цікавить, і розмір вибірки?

Відповідь: Група інтересів - це плитки голосних літер. Розмір групи, що цікавить - 44. Розмір проби дорівнює семи.

Приклад\(\PageIndex{2}\)

Припустимо, що партія 100 DVD-плеєрів, як відомо, має десять дефектних плеєрів. Інспектор випадковим чином вибирає 12 для перевірки. Він зацікавлений у визначенні ймовірності того, що серед 12 гравців не більше двох є дефектними. Дві групи - це 90 недефектних DVD-плеєрів та 10 дефектних DVD-плеєрів. Група інтересів (перша група) є дефектною групою, оскільки питання ймовірності запитує ймовірність щонайменше двох дефектних DVD-плеєрів. Розмір зразка - 12 DVD-плеєрів. (Вони можуть бути недефектними або несправними.) Нехай\(X =\) кількість несправних DVD-плеєрів в зразку 12. \(X\)приймає на себе значення\(0, 1, 2, \dotsc, 10\). \(X\)може не приймати значення 11 або 12. Розмір вибірки 12, але є тільки 10 дефектних DVD-плеєрів. Напишіть заяву ймовірності математично.

Відповідь

\(P(x \leq 2)\)

Вправа\(\PageIndex{2}\)

Брутто яєць містить 144 яєць. Відомо, що конкретний грубий має 12 тріснутих яєць. Інспектор випадковим чином вибирає 15 для перевірки. Вона хоче знати ймовірність того, що серед 15 щонайбільше три тріснуті. Що таке\(X\), і які значення воно набуває?

Відповідь: Нехай\(X =\) кількість тріснутих яєць в пробі 15. \(X\)приймає на себе значення\(0, 1, 2, \dotsc, 12\).

Приклад\(\PageIndex{3}\)

Ви є президентом організації спеціальних заходів на кампусі. Вам потрібен комітет з семи студентів, щоб спланувати спеціальний день народження для президента коледжу. Ваша організація складається з 18 жінок і 15 чоловіків. Вас цікавить кількість чоловіків у вашому комітеті. Якщо члени комітету вибираються випадковим чином, яка ймовірність того, що у вашому комітеті більше чотирьох чоловіків?

Це гіпергеометрична проблема, тому що ви обираєте свій комітет з двох груп (чоловіків і жінок).

Ви вибираєте з заміною або без неї?
Що являє собою група інтересів?
Скільки в групі за інтересами?
Скільки в іншій групі?
Нехай\(X =\) _________ на комітет. Які значення\(X\) набуває?
Питання ймовірності\(P(\) _______\()\).

Рішення

без
чоловіки
15 чоловіків
18 жінок
Нехай\(X =\) кількість чоловіків в комітеті. \(x = 0, 1, 2, \dotsc, 7\).
\(P(x > 4)\)

Вправа\(\PageIndex{3}\)

Палітра налічує 200 молочних коробок. З 200 коробок відомо, що десять з них просочилися і не можуть бути продані. Клерк акцій випадковим чином вибирає 18 для перевірки. Він хоче знати ймовірність того, що серед 18 не більше двох протікають. Наведіть п'ять причин, чому це гіпергеометрична проблема.

Відповідь

Виділяють дві групи.
Вас турбує група інтересів.
Ви зразок без заміни.
Кожна пікіровка не є самостійною.
Ви не маєте справу з випробуваннями Бернуллі.

Позначення для гіпергеометричного:\(H =\) Hypergeometric Probability Distribution Function

\[X \sim H(r, b, n)\]

Прочитайте це як "\(X\)є випадковою величиною з гіпергеометричним розподілом.» Параметрами є\(r, b\), і\(n\);\(r =\) розмір групи, що цікавить (перша група),\(b =\) розмір другої групи,\(n =\) розмір обраної вибірки.

Приклад\(\PageIndex{4}\)

Комітет шкільного сайту повинен бути обраний випадковим чином з шести чоловіків і п'яти жінок. Якщо комітет складається з чотирьох членів, обраних випадковим чином, то яка ймовірність того, що двоє з них - чоловіки? Скільки чоловіків ви очікуєте бути в комітеті?

Нехай\(X\) = кількість чоловіків на комітеті з чотирьох. Чоловіки - група інтересів (перша група).

\(X\)приймає на себе значення\(0, 1, 2, 3, 4\), де\(r = 6, b = 5\), і\(n = 4\). \(X \sim H(6, 5, 4)\)

Знайти\(P(x = 2)\). \(P(x = 2) = 0.4545\)(калькулятор або комп'ютер)

В даний час TI-83+ і TI-84 не мають гіпергеометричних функцій ймовірності. Існує ряд комп'ютерних пакетів, включаючи Microsoft Excel, які роблять.

Імовірність того, що в комітеті двоє чоловіків, становить близько 0,45.

Графік\(X \sim H(6, 5, 4)\) - це:

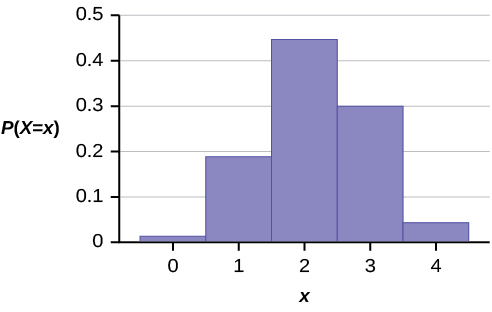
Цей графік показує гіпергеометричний розподіл ймовірностей. Він має п'ять барів, які трохи нормально розподілені. Вісь x показує значення від 0 до 4 з кроком 1, представляючи кількість чоловіків у комітеті з чотирьох осіб. Вісь Y коливається від 0 до 0,5 з кроком 0,1. — Малюнок\(\PageIndex{1}\).

Вісь y містить ймовірність того\(X\), де\(X =\) число чоловіків на комітеті.

Ви очікуєте\(m = 2.18\) (близько двох) чоловіків у комітеті.

Формула середнього значення дорівнює

\[\mu = \frac{nr}{r+b} \frac{(4)(6)}{6+5} = 2.18\]

Вправа\(\PageIndex{4}\)

Очна баскетбольна команда повинна бути обрана випадковим чином з 15 хлопчиків і 12 дівчаток. У команді десять слотів. Ви хочете знати ймовірність того, що вісім гравців будуть хлопцями. Що таке група інтересів і зразок?

Відповідь: Група інтересів - 15 хлопчиків. Вибірка складається з десяти слотів на очної баскетбольній команді.

Резюме

Гіпергеометричний експеримент - це статистичний експеримент з наступними властивостями:

Ви берете проби з двох груп.
Вас турбує група за інтересами, яка називається першою групою.
Ви вибірку без заміни з комбінованих груп.
Кожен підбір не є самостійним, так як відбір проб проводиться без заміни.
Ви не маєте справу з випробуваннями Бернуллі.

Результати гіпергеометричного експерименту відповідають гіпергеометричному розподілу ймовірностей. Випадкова величина\(X\) = кількість елементів з групи, що цікавить. Розподіл\(X\) позначається\(X \sim H(r, b, n)\), де\(r =\) розмір цікавить групи (перша група),\(b =\) розмір другої групи, а\(n =\) також розмір обраної вибірки. Звідси випливає, що\(n \leq r + b\). Середнє значення\(X\) є\(\mu = \frac{nr}{r+b}\) і стандартне відхилення є\(\sigma = \sqrt{\frac{rbn(r+b-n)}{(r+b)^{2}(r+b-1)}}\).

Огляд формули

\(X \sim H(r, b, n)\)означає, що дискретна випадкова величина\(X\) має гіпергеометричний розподіл ймовірностей з\(r =\) розміром групи інтересів (першої групи),\(b =\) розміром другої групи та\(n =\) розміром обраної вибірки.

\(X\)= кількість позицій з групи інтересів, які знаходяться в обраній вибірці, і\(X\) можуть приймати значення\(x = 0, 1, \dotsc,\) до розміру цікавить групи. (У деяких випадках мінімальне значення для\(X\) може бути більшим за нуль.)

\(n \leq r + b\)

Середнє значення\(X\) задається за формулою,\(\mu = \frac{nr}{r+b}\) а стандартне відхилення -\(= \sqrt{\frac{rbn(r+b-n)}{(r+b)^{2}(r+b-1)}}\).

Використовуйте наступну інформацію, щоб відповісти на наступні п'ять вправ: Припустимо, що група студентів статистики розділена на дві групи: бізнес-спеціальності та некомерційні спеціальності. У групі 16 бізнес-спеціальностей і сім неділових спеціальностей в групі. Береться випадкова вибірка з дев'яти студентів. Нас цікавить кількість бізнес-спеціальностей у вибірці.

Вправа\(\PageIndex{5}\)

У словах визначаємо випадкову величину\(X\).

Відповідь

\(X =\)кількість бізнес-спеціальностей у вибірці.

Вправа\(\PageIndex{6}\)

\(X \sim\)_____ (_____, _____)

Вправа\(\PageIndex{7}\)

Які значення\(X\) набуває?

Відповідь

\(2, 3, 4, 5, 6, 7, 8, 9\)

Вправа\(\PageIndex{8}\)

Знайдіть стандартне відхилення.

Вправа\(\PageIndex{9}\)

В середньому (\(\mu\)), скільки ви очікуєте бути бізнес-майорів?

Відповідь

6.26

Глосарій

Гіпергеометричний експеримент

статистичний експеримент з наступними властивостями:

Ви берете проби з двох груп.
Вас турбує група за інтересами, яка називається першою групою.
Ви вибірку без заміни з комбінованих груп.
Кожен підбір не є самостійним, так як відбір проб проводиться без заміни.
Ви не маєте справу з випробуваннями Бернуллі.

Гіпергеометрична ймовірність

дискретна випадкова величина (RV), яка характеризується:

Фіксована кількість випробувань.
Імовірність успіху не однакова від судового розгляду до суду.

Ми вибірки з двох груп предметів, коли нас цікавить лише одна група. \(X\)визначається як кількість успіхів із загальної кількості обраних предметів. \(r =\)Позначення:\(X \sim H(r, b, n)\), де кількість позицій в групі цікавить,\(b =\) кількість елементів в групі не цікавить, і\(n =\) кількість обраних елементів.