16.3: Сходи влади Туреччини
- Page ID
- 98215
Цілі навчання
- Дайте Туреччині сходи перетворень
- Знайдіть трансформацію, яка виявляє лінійну залежність
- Знайти перетворення для наближення нормального розподілу
Вступ
Ми припускаємо, що у нас є колекція двоваріантних даних.
\[(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\]
і що нас цікавить взаємозв'язок між змінними\(x\) і\(y\). Побудова даних на діаграмі розсіювання - перший крок. Як приклад розглянемо населення США за\(200\) роки до Громадянської війни. Звичайно, багаторічний перепис почався в\(1790\). Ці дані нанесені двома способами на рис\(\PageIndex{1}\). Мальтус прогнозував, що геометричне зростання популяцій у поєднанні з арифметичним зростанням виробництва зерна матиме катастрофічні результати. Дійсно, населення США слідувало за експоненціальною кривою в цей період.
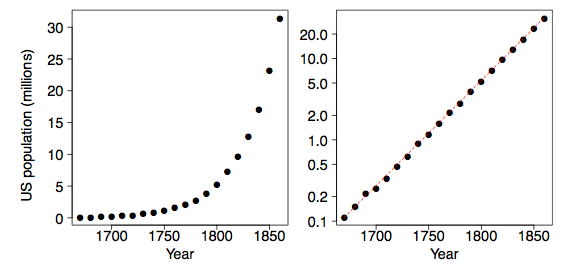
Сходи трансформації Туреччини
Tukey (\(1977\)) описує впорядкований спосіб повторного вираження змінних за допомогою силового перетворення. Можливо, вам знайома поліноміальна регресія (форма множинної регресії), в якій проста лінійна модель\(y = b_0 + b_1X\) розширюється такими термінами, як\(b_2X^2 + b_3X^3 + b_4X^4\). Крім того, Туреччина пропонує вивчити прості стосунки, такі як
\[y = b_0 + b_1X^λ\]
або
\[y^λ = b_0 + b_1X \label{eq1}\]
де\(λ\) - параметр, обраний для того, щоб співвідношення було максимально наближено до прямої. Лінійні відносини є особливими, і якщо перетворення типу\(x^\lambda\) або y λ працює як в Equation\ ref {eq1}, то ми повинні розглянути можливість зміни нашої шкали вимірювання для решти статистичного аналізу.
Немає обмежень на цінності\(λ\), які ми можемо розглянути. Очевидно вибір\(λ = 1\) залишає дані незмінними. Негативні значення також\(λ\) є розумними. Наприклад, відносини
\[y = b_0 + \dfrac{b_1}{x}\]
буде представлений\(λ = −1\). Значення не\(λ = 0\) має особливого значення, так як\(X^0 = 1\), яка є всього лише постійною. Tukey (\(1977\)) припускає, що зручно просто визначити перетворення, коли\(λ = 0\) буде функція логарифма, а не константа\(1\). Незабаром ми переглянемо цю конвенцію. У наступній таблиці наведені приклади сходів перетворень Туреччини.
| \(\lambda\) | \(-2\) | \(-1\) | \(-1/2\) | \(0\) | \(1/2\) | \(1\) | \(2\) |
| \(y\) | \(\tfrac{1}{x^2}\) | \(\tfrac{1}{x}\) | \(\tfrac{1}{\sqrt{x}}\) | \(\log x\) | \(\sqrt{x}\) | \(x\) | \(x^2\) |
Якщо\(x\) приймає негативні значення, то необхідно дотримуватися особливої обережності, щоб перетворення мали сенс, якщо це можливо. Ми, як правило, обмежуємося змінними, де\(x > 0\) уникнути цих міркувань. Для деяких залежних змінних, таких як кількість помилок, зручно додавати\(1\) до\(x\) перед застосуванням перетворення.
Також, якщо параметр перетворення\(λ\) негативний, то перетворена змінна\(x^\lambda\) змінюється. Наприклад, якщо\(x\) збільшується, то\(1/x\) зменшується. Ми вирішили перевизначити трансформацію Туреччини, щоб бути\(-x^\lambda\) якщо для\(λ < 0\) того, щоб зберегти порядок змінної після перетворення. Формально трансформація Туреччини визначається як
\[y=\left\{\begin{matrix} x^\lambda & if & \lambda >0\\ \log x & if & \lambda =0\\ -(x^\lambda) & if & \lambda <0 \end{matrix}\right.\]
У таблиці\(\PageIndex{2}\) ми відтворюємо таблицю,\(\PageIndex{1}\) використовуючи змінене визначення, коли\(λ < 0\).
| \(\lambda\) | \(-2\) | \(-1\) | \(-1/2\) | \(0\) | \(1/2\) | \(1\) | \(2\) |
| \(y\) | \(\tfrac{-1}{x^2}\) | \(\tfrac{-1}{x}\) | \(\tfrac{-1}{\sqrt{x}}\) | \(\log x\) | \(\sqrt{x}\) | \(x\) | \(x^2\) |
Найкраща трансформація для лінійності
Мета полягає в тому, щоб знайти значення\(λ\), яке робить діаграму розсіювання якомога лінійнішою. Для населення США логарифмічне перетворення, застосоване до,\(y\) робить відносини майже ідеально лінійними. Червона пунктирна лінія в правій рамці малюнка\(\PageIndex{1}\) має нахил приблизно\(1.35\); тобто населення США зростало зі швидкістю приблизно\(35\%\) за десятиліття.
Логарифмічне перетворення відповідає вибору\(λ = 0\) за угодою Тукі. На малюнку\(\PageIndex{2}\) ми показуємо діаграму розкиду даних населення США\(λ = 0\) як для, так і для інших варіантів\(λ\).
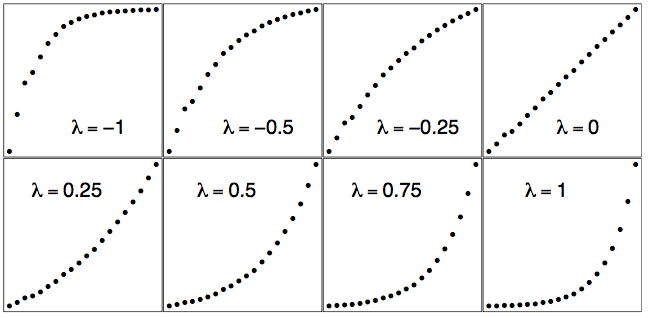
Сирі дані відображаються в правому нижньому кадрі малюнка,\(\PageIndex{2}\) коли\(λ = 1\). Логарифмічна посадка знаходиться у верхньому правому кадрі, коли\(λ = 0\). Зверніть увагу, як діаграма розсіювання плавно перетворюється від опуклої до увігнутої зі\(λ\) збільшенням. Таким чином, інтуїтивно існує унікальний кращий вибір,\(λ\) відповідний «найбільш лінійному» графіку.
Один із способів зробити цей вибір об'єктивним - використовувати для цієї мети об'єктивну функцію. Один підхід може полягати в тому, щоб підігнати пряму лінію до перетворених точок і спробувати мінімізувати залишки. Однак більш простий підхід заснований на тому, що коефіцієнт кореляції\(r\), є мірою лінійності діаграми розсіювання. Зокрема, якщо точки потрапляють на пряму, то їх співвідношення буде\(r = 1\). (Нам не потрібно турбуватися про випадок, коли,\(r = −1\) оскільки ми визначили перетворену змінну Тукі,\(x_\lambda\) щоб бути позитивно корельованою з\(x\) собою.)
На\(\PageIndex{3}\) малюнку побудовано коефіцієнт кореляції діаграми розсіювання\((x,y_\lambda )\) як функція\(λ\). Зрозуміло, що логарифмічне перетворення (\(λ = 0\)) є майже оптимальним за цим критерієм.
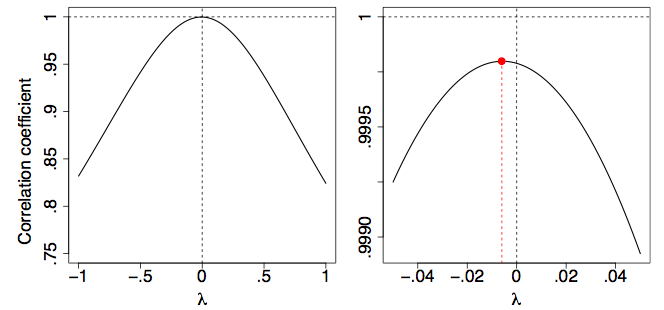
Чи населення США все ще перебуває на тій же експоненціальній моделі зростання? На малюнку\(\PageIndex{4}\) ми показуємо населення США від\(1630\) до\(2000\) використання трансформації та підгонки, що використовуються у правій рамці малюнка\(\PageIndex{1}\). На щастя, експоненціальне зростання (або принаймні його темпи) не було витримано в ХХ столітті. Якби це було, населення США за рік було\(2000\) б понад\(2\) мільярд (\(2.07\)а точніше), більше, ніж населення Китаю.
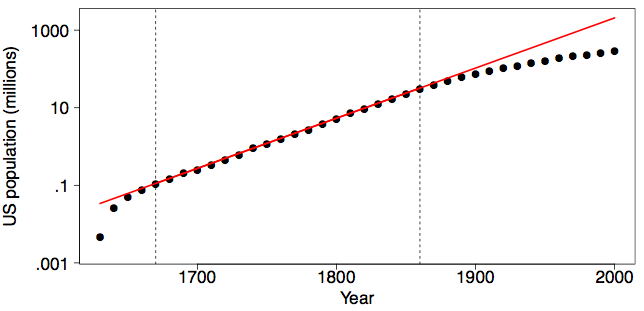
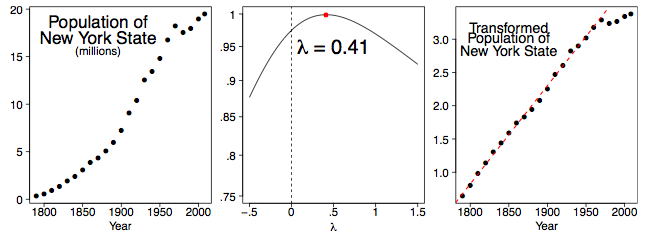
Ми також можемо вивчити цифри десятирічного перепису населення окремих держав. На\(\PageIndex{5}\) малюнку виводимо дані про населення штату Нью-Йорк від\(1790\) до\(2000\), разом з оцінкою чисельності населення в\(2008\). Очевидно, що щось незвичайне сталося починаючи з\(1970\). (Це почалося період масової міграції на Захід і Південь, коли промисловості іржі пояса почали закриватися.) Таким чином, ми обчислюємо найкраще\(λ\) значення, використовуючи дані з\(1790\) -\(1960\) в середньому кадрі Figure\(\PageIndex{5}\). Правий кадр відображає перетворені дані разом з лінійним підгонкою за\(1790-1960\) період. Значення не\(λ = 0.41\) є очевидним, і можна розумно вибрати\(λ = 0.50\) для використання з практичних міркувань.
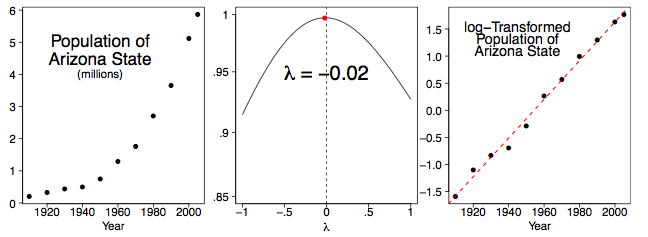
Якщо ми подивимося на одне з молодших штатів на Заході, то картина інша. Арізона привернула багатьох пенсіонерів і іммігрантів. Малюнок\(\PageIndex{6}\) підсумовує наші висновки. Дійсно, зростання населення в Арізоні є логарифмічним, і, здається, все ще є логарифмічним\(2005\).
Зменшення перекісу
Багато статистичні методи, такі як\(t\) тести та аналіз дисперсії, припускають нормальні розподіли. Хоча ці методи відносно стійкі до порушень нормальності, перетворення розподілів для зменшення перекосу може помітно збільшити їх потужність.
Як приклад, дані в прикладі «Стереограми» дуже перекошені. Тест різниці між двома умовами з використанням вихідних даних призводить до p значення\(0.056\), значення, яке умовно не вважається значущим. Однак після перетворення колоди (\(λ = 0\)), що значно зменшує перекіс,\(p\) значення умовно вважається значним.\(0.023\)
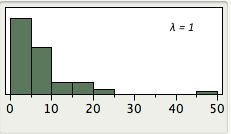
Демонстрація на малюнку\(\PageIndex{7}\) показує розподіли даних із тематичного дослідження Stereograms, перетворених з різними значеннями\(λ\). Зменшення\(λ\) робить розподіл менш позитивним перекосом. Майте на увазі, що\(λ = 1\) це необроблені дані. Зверніть увагу, що існує незначний позитивний перекіс,\(λ = 0\) але набагато менший перекіс, ніж у вихідних даних (\(λ = 1\)). Значення нижче 0 призводять до негативного перекосу.
Посилання
Туреччина, Дж. (1977). Розвідувальний аналіз даних. Аддісон-Уеслі, Редінг, Массачусетс.
