Skip to main content
LibreTexts - Ukrayinska

15.E: Аналіз дисперсії (вправи)

  1. Last updated
  2. Save as PDF
  • Page ID
    98190

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Загальні питання

    Q1

    Що таке нульова гіпотеза перевірена аналізом дисперсії?

    Q2

    Які припущення щодо аналізу дисперсії між суб'єктами?

    Q3

    Що таке змінна між суб'єктами?

    Q4

    Чому б просто не обчислити\(t\) -тести серед усіх пар засобів замість обчислення аналізу дисперсії?

    Q5

    У чому різниця між "\(N\)" і "\(n\)«?

    Q6

    Як це, що оцінки дисперсії можуть бути використані для перевірки гіпотези про засоби?

    Q7

    Поясніть, чому дисперсія вибіркових засобів повинна бути помножена на\(n\) "" при обчисленні\(MSB\).

    Q8

    Який перекіс має\(F\) розподіл?

    Q9

    Коли роблять\(MSB\) і\(MSE\) оцінюють однакову кількість?

    Q10

    Якщо експеримент проводиться з\(6\) умовами і\(5\) суб'єктами в кожному стані, що таке\(dfn\) і\(dfe\)?

    Q11

    Як на форму\(F\) розподілу впливають ступені свободи?

    Q12

    Які дві складові загальної суми квадратів в однофакторному дизайні між предметами?

    Q13

    Як обчислюється середній квадрат з суми квадратів?

    Q14

    Експериментатор зацікавлений у впливі двох незалежних змінних на самооцінку. Що краще в проведенні факторіального експерименту, ніж проведення двох окремих експериментів, по одному для кожної незалежної змінної?

    Q15

    Проведено експеримент щодо впливу віку та стану лікування (експериментального проти контрольного) на швидкість читання. Який статистичний термін (основний ефект, простий ефект, взаємодія, конкретне порівняння) застосовується до кожного з описів ефектів.

    1. Ефект від лікування був більший для\(15\) -річних дітей, ніж це було для\(5\) - або\(10\) -річних.
    2. Загалом, суб'єкти в стані лікування виконувалися швидше, ніж суб'єкти в контрольному стані.
    3. Різниця між\(10\) - і\(15\) -річними малюками була значною за умови лікування.
    4. Різниця між\(15\) - річними та середніми показниками\(5\) - і\(10\) -річними була значною.
    5. У міру дорослішання діти швидше читають.

    Q16

    Проаналізовано\(A(3) \times B(4)\) факторіальний дизайн з\(6\) предметами в кожній групі. Дайте джерело і ступені свободи стовпців аналізу дисперсії зведеної таблиці.

    Q17

    Наступні дані взяті з гіпотетичного дослідження впливу віку та часу на бали на тест розуміння читання. Обчислити аналіз дисперсії зведеної таблиці.

    12-річні діти 16-річні діти
    30 хвилин 66
    68
    59
    72
    46    		 74
    71
    67
    82
    76
    60 хвилин 69
    61
    69
    73
    61    		 95
    92
    95
    98
    94

    Q18

    Визначте «Тристороння взаємодія»

    КВАРТАЛ 19

    Визначте взаємодію з точки зору простих ефектів.

    Q20

    Графік взаємодії для\(A(2) \times B(2)\) дизайну, в якому ефект більше\(A1\), ніж на\(A2\).\(B\) Залежною змінною є «Число правильно». Переконайтеся, що позначені обидві осі.

    Q21

    Нижче наведено два графіки чисельності засобів для\(2 \times 3\) конструкцій. Для кожного графіка вкажіть, який ефект (и) (\(A\)\(B\), або\(A \times B\)) є ненульовими.

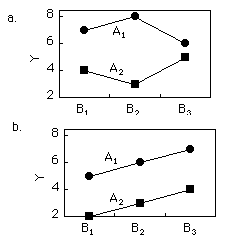
    q8ch13.gif

    Q22

    Наступні дані взяті з\(A(2) \times B(4)\) факторіального дизайну.

    B1 B2 B3 B4
    A1 1
    3
    4
    5    		 2
    2
    4
    5    		 3
    4
    2
    6

    4
    5
    6
    8
    A2 1
    1
    2
    2    		 2
    3
    2
    4    		 4
    6
    7
    8    		 8
    9
    9
    8
    1. Обчислити аналіз дисперсії.
    2. Тестові відмінності між чотирма рівнями\(B\) використання корекції Бонферроні.
    3. Перевірте лінійну складову тренду на ефект\(B\).
    4. Побудуйте взаємодію.
    5. Опишіть взаємодію словами.

    Q23

    Чому конструкції всередині предметів зазвичай більш потужні, ніж дизайн між предметами?

    Q24

    Яке джерело варіації знаходиться в зведеній таблиці ANOVA для дизайну всередині предметів, який не міститься в зведеній таблиці ANOVA для дизайну між предметами. Що відбувається з цим джерелом варіації в дизайні між предметами?

    Q25

    Наступні дані містять по три бали з кожного з п'яти предметів. Три бали на предмет - це їх оцінки на трьох випробуваннях завдання пам'яті.

    \[\begin{matrix} 4 & 6 & 7\\ 3 & 7 & 7\\ 2 & 8 & 5\\ 1 & 4 & 7\\ 4 & 6 & 9 \end{matrix}\]

    1. Обчислення та ANOVA
    2. Перевірте всі попарні відмінності між засобами за допомогою тесту Бонферроні на\(0.01\) рівні.
    3. Перевірте лінійну та квадратичну складові тренду для цих даних.

    Q26

    Дайте стовпці джерела та df зведеної таблиці ANOVA для наступних експериментів:

    1. \(22\)суб'єкти перевіряються на простому завданні часу реакції і на вибір часу реакції завдання.
    2. \(12\)Чоловічі та\(12\) жіночі суб'єкти перевіряються під трьома рівнями дозування препарату:\(0 mg, 10 mg, 20 mg\).
    3. \(20\)випробовувані тестуються на руховому навчальному завданні для\(3\) випробувань в день протягом\(2\) декількох днів.
    4. Проводиться експеримент, в якому депресивним людям або призначають групу медикаментозної терапії, групу поведінкової терапії, або в контрольну групу. \(10\)суб'єкти закріплюються за кожною групою. Рівень вимірюється один раз на місяць протягом\(4\) місяців.

    Питання з тематичних досліджень

    Наступне питання з тематичного дослідження Stroop Interference.

    Q27

    У наборі даних є бали (раз) для чоловіків і жінок за кожне з трьох завдань.

    1. Зробіть\(Gender (2) \times Task (3)\) аналіз на дисперсію.
    2. Побудуйте взаємодію.

    Наступне питання з тематичного дослідження лікування СДУГ.

    Q28

    Дані мають чотири бали на предмет.

    1. Чи є дизайн між предметами або всередині предметів?
    2. Створіть зведену таблицю ANOVA.

    Наступне питання з тематичного дослідження Angry Moods.

    Q29

    Використовуючи індекс вираження гніву як залежну змінну, виконайте\(2 \times 2\) ANOVA з гендерною та спортивною участю як двома факторами. Чи значно відрізняються спортсмени та неспортсмени тим, наскільки гніву вони висловлюють? Чи суттєво відрізняються статі за індексом вираження гніву? Чи значно відрізняється ефект від спортивної участі для двох статей?

    Наступне питання з тематичного дослідження «Зброя та агресія».

    Q30

    Обчислити\(2 \times 2\) ANOVA на цих даних з наступними двома факторами: простий тип (було перше слово зброєю чи ні?) і словотип (було друге слово агресивним або неагресивним?). Уважно подумайте, чи є змінні між змінними суб'єкта або всередині суб'єктів.

    Наступне питання з тематичного дослідження «Посмішки та поблажливість».

    Q31

    Обчислити зведену таблицю ANOVA.