15.5: Багатофакторний між суб'єктами
- Page ID
- 98178
Цілі навчання
- Визначте основний ефект, простий ефект, взаємодію та граничне середнє
- Створіть взаємозв'язок між простими ефектами та взаємодією
- Обчислити джерело варіації та df для кожного ефекту в факторіальному дизайні
- Змова на засоби для взаємодії
- Визначте тристоронню взаємодію
Основні поняття і терміни
У тематичному дослідженні «Упередженість проти партнерів ожиріння» дослідники були зацікавлені в тому, чи впливає вага супутника претендента на роботу судження про кваліфікацію заявника чоловічої статі на роботу. Досліджено дві незалежні змінні:
- чи був супутник ожирінням або типовою вагою і
- чи був супутник подругою або просто знайомим.
Одним з підходів могло бути проведення двох окремих досліджень, по одному з кожною незалежною змінною. Однак ефективніше провести одне дослідження, яке включає обидві незалежні змінні. Більше того, існує набагато більша перевага, ніж ефективність для включення двох змінних в одне дослідження: це дозволяє перевірити взаємодію між змінними. Відбувається взаємодія, коли ефект однієї змінної відрізняється в залежності від рівня другої змінної. Наприклад, можливо, що ефект від наявності супутника з ожирінням буде відрізнятися залежно від стосунків із супутником. Можливо, існує більше упереджень щодо людини з ожирінням супутником, якщо супутник - подруга, ніж якщо вона просто знайома. Якщо так, то була б взаємодія між фактором ожиріння та фактором взаємозв'язку.
У цьому експерименті є три ефекти, що представляють інтерес:
- Вага: Чи оцінюють заявників по-різному залежно від ваги свого супутника?
- Відносини: Чи оцінюють заявників по-різному залежно від їхніх стосунків із супутником?
- Вага x Взаємодія відносин: Чи відрізняється вплив ваги залежно від відносин з супутником?
Перші два ефекти (Вага і Відносини) є обома основними ефектами. Основним ефектом незалежної змінної є ефект усереднення змінної над рівнями інших змінних. Зручно говорити про основні ефекти в плані граничних засобів. Крайовим середнім для рівня змінної є середнє значення середніх всіх рівнів іншої змінної. Наприклад, граничне середнє для рівня «Ожиріння» - це середнє значення «Подруга з ожирінням» і «Знайомство з ожирінням». Таблиця\(\PageIndex{1}\) показує, що це граничне середнє дорівнює середньому\(5.65\) і\(6.15\), яке є\(5.90\). Аналогічно граничне середнє для рівня «Типовий» - це середнє значення\(6.19\) і\(6.59\), яке є\(6.39\). Основний ефект Weight заснований на порівнянні цих двох граничних засобів. Аналогічним чином граничними засобами для «Подруга» і «Знайомство» є\(5.92\) і\(6.37\).
| Вага компаньйона | ||||
|---|---|---|---|---|
| ожиріння | Типові | граничне середнє значення | ||
| Відносини | Подруга | 5.65 | 6.19 | 5.92 |
| Знайомство | 6.15 | 6.59 | 6.37 | |
| граничне середнє значення | 5.90 | 6.39 | ||
На відміну від основного ефекту, який є ефектом змінної, усередненої між рівнями іншої змінної, простим ефектом змінної є ефект змінної на одному рівні іншої змінної. Простий ефект ваги на рівні «Подруга» - це різниця між умовами «Подруга Типова» та «Подруга ожиріння». Різниця полягає в тому\(6.19-5.65 = 0.54\). Аналогічно, простий ефект ваги на рівні «Знайомство» - це різниця між умовами «Знайомство Типове» і «Знайомство з ожирінням». Різниця полягає в тому\(6.59-6.15 = 0.44\).
Нагадаємо, що відбувається взаємодія, коли ефект однієї змінної відрізняється в залежності від рівня іншої змінної. Це еквівалентно тому, що існує взаємодія, коли прості ефекти відрізняються. У цьому прикладі прості ефекти ваги є\(0.54\) і\(0.44\). Як показано нижче, ці прості ефекти істотно не відрізняються.
Тести значущості
Важливими питаннями є не те, чи є основні ефекти та взаємодії у вибіркових даних. Натомість важливо те, що вибіркові дані дозволяють зробити висновок про населення. Тут приходить аналіз дисперсії. ANOVA перевіряє основні ефекти та взаємодії на значущість. Зведена таблиця ANOVA для цих даних наведена в табл\(\PageIndex{2}\).
| Джерело | дф | SSQ | МС | F | р |
|---|---|---|---|---|---|
| Вага | 1 | 10.4673 | 10.4673 | 6.214 | 0.0136 |
| Відносини | 1 | 8.8144 | 8.8144 | 5.233 | 0.0234 |
| Ш х Р | 1 | 0,1038 | 0,1038 | 0.062 | 0.8043 |
| Помилка | 172 | 289.7132 | 1.6844 | ||
| Всього | 175 | 310.1818 |
Розглянемо спочатку ефект «Вага». Ступінь свободи (\(df\)) для «Вага» є\(1\). Ступінь свободи для основного ефекту завжди дорівнює кількості рівнів змінної мінус одиниця. Оскільки існує два рівні змінної «Вага» (типовий і ожиріння), то\(df\) є\(2 - 1 = 1\). Пропускаємо обчислення суми квадратів (\(SSQ\)) не тому, що це складно, а тому, що так набагато простіше покладатися на комп'ютерні програми для її обчислення. Середній квадрат (\(MS\)) - це сума квадратів, поділених на\(df\). \(F\)Коефіцієнт обчислюється шляхом ділення\(MS\) ефекту for на помилку\(MS\) for (\(MSE\)). Для ефекту «Вага»,\(F = 10.4673/1.6844 = 6.214\). Останній стовпець - це ймовірність отримати\(F\)\(6.214\) або більше\(p\), враховуючи, що немає ефекту ваги в популяції. \(p\)Значення є\(0.0136\) і тому нульова гіпотеза про відсутність основного ефекту «Вага» відхиляється. Висновок полягає в тому, що супроводження супутника з ожирінням знижує судження про кваліфікацію.
Ефект «Відношення» тлумачиться так само. Висновок полягає в тому, що супроводження подруги призводить до нижчих оцінок, ніж супровід знайомого.
\(df\)Для взаємодії є добутком\(df's\) змінних у взаємодії. Для взаємодії «Вага x Relation» (\(W \times R\)),\(df = 1\) оскільки і вага, і відношення мають один\(df: 1 \times 1 = 1\). \(p\)Значення взаємодії полягає в тому\(0.8043\), що ймовірність отримання взаємодії більшою або більшою за ту, яка отримана в експерименті, якщо не було взаємодії в популяції. Тому ці дані не дають жодних доказів взаємодії. Завжди майте на увазі, що відсутність доказів ефекту не виправдовує висновку про відсутність ефекту. Іншими словами, ви не приймаєте нульову гіпотезу тільки тому, що не відкидаєте її.
Для «Помилка» ступінь свободи дорівнює загальній кількості спостережень мінус загальна кількість груп. Розміри вибірки чотирьох умов в цьому експерименті наведені в табл\(\PageIndex{3}\). Загальна кількість спостережень становить\(40 + 42 + 40 + 54 = 176\). Так як існує чотири групи,\(dfe = 176 - 4 = 172\).
| Вага компаньйона | |||
|---|---|---|---|
| ожиріння | Типові | ||
| Відносини | Подруга | 40 | 42 |
| Знайомство | 40 | 54 | |
Останній рядок у Зведеній таблиці ANOVA - «Всього». Ступінь свободи загальна дорівнює сумі всіх ступенів свободи. Вона також дорівнює\(\textit{number of observations minus 1}\), або\(176 - 1 = 175\). Коли є рівні розміри вибірки, сума квадратів total буде дорівнює сумі всіх інших сум квадратів. Однак, коли є нерівні розміри вибірки, як тут, це взагалі не буде правдою. Причини цього складні і розглядаються в розділі Нерівні розміри вибірки.
Засоби побудови графіків
Хоча сюжет, показаний на малюнку,\(\PageIndex{1}\) ілюструє основні ефекти, а також взаємодію (або відсутність взаємодії), він називається сюжетом взаємодії. Важливо уважно продумати складові цієї змови. По-перше, залежна змінна знаходиться на\(Y\) -осі. По-друге, одна з незалежних змінних знаходиться на\(X\) -осі. В даному випадку це змінна «Вага». Нарешті, для кожного рівня іншої незалежної змінної проводиться окрема лінія. Краще позначати лінії прямо на графіку, як показано тут, ніж легендою.
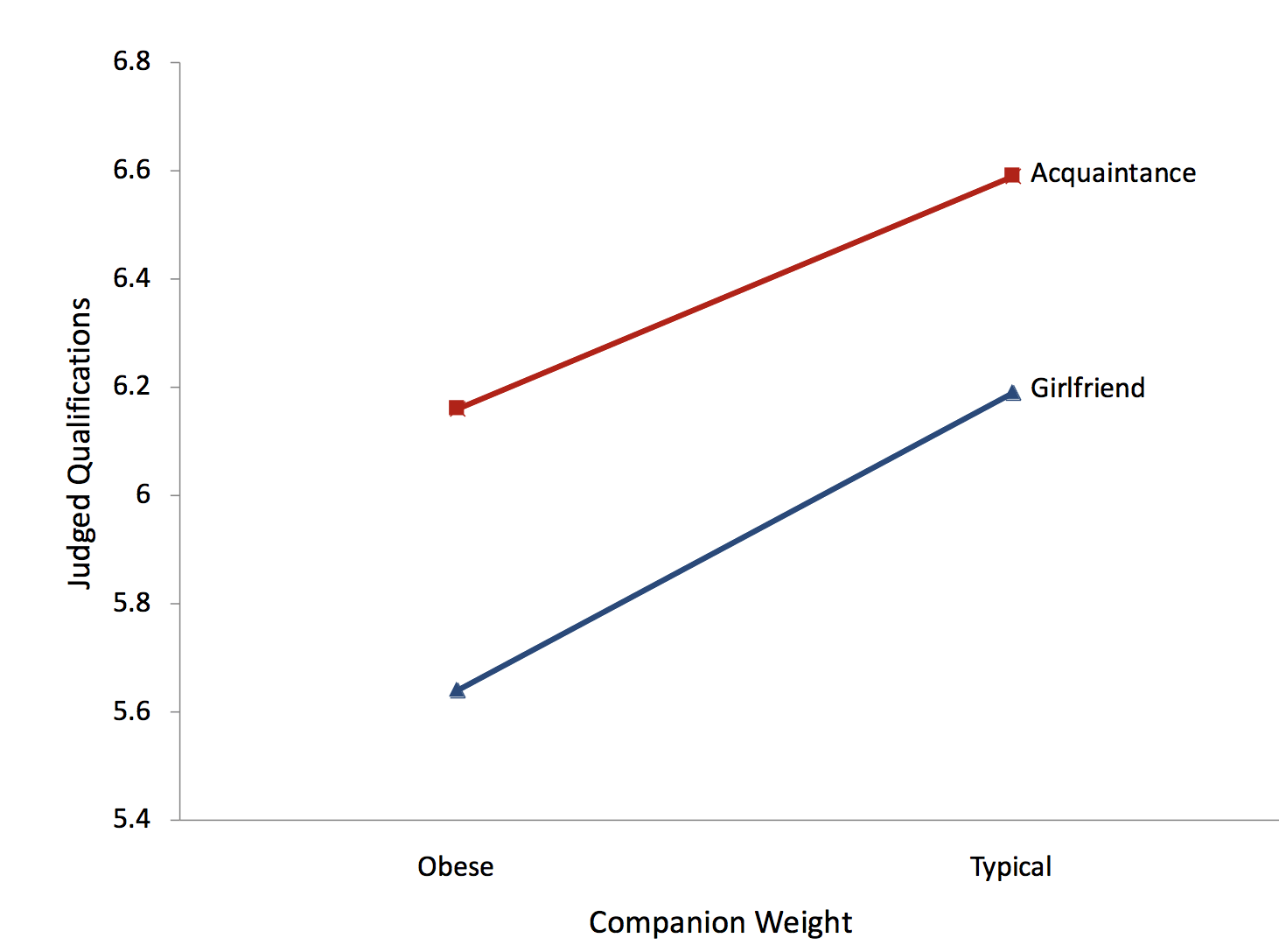
Якщо у вас три або більше рівнів на\(X\) -осі, ви не повинні використовувати лінії, якщо немає числового впорядкування рівнів. Якщо ваша змінна на\(X\) -осі є якісною змінною, ви можете використовувати графік, такий як той, що на рис\(\PageIndex{2}\). Однак, як обговорювалося в розділі про гістограмах, краще було б замінити кожен бар коробчатим графіком.
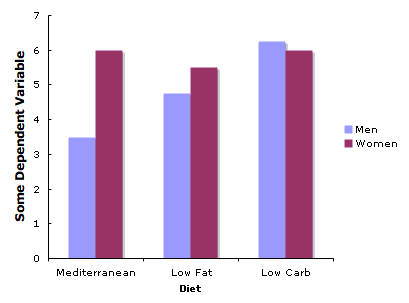
На малюнку\(\PageIndex{3}\) показаний такий сюжет. Зверніть увагу, як він містить інформацію про медіани, квантилі та мінімуми та максимуми, які не містяться на малюнку\(\PageIndex{2}\). Найголовніше, ви отримуєте уявлення про те, наскільки розподіли перекриваються з малюнка\(\PageIndex{3}\), чого ви не отримаєте з рис\(\PageIndex{2}\).
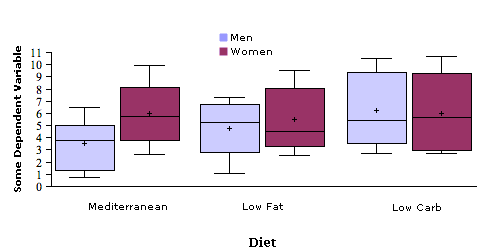
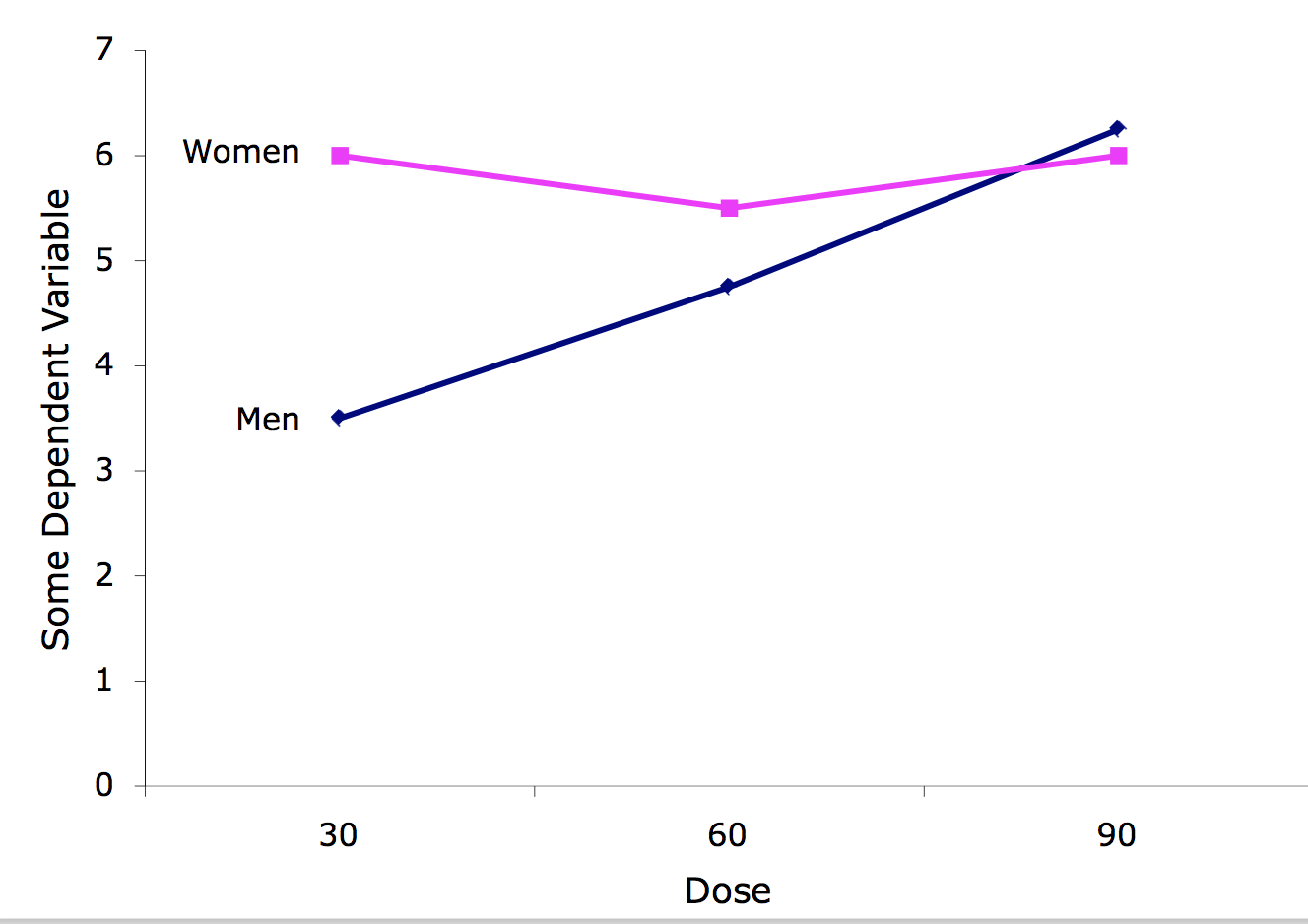
Лінійні графіки - хороший варіант, коли існує більше двох рівнів числової змінної. На\(\PageIndex{4}\) малюнку наведено приклад. Лінійний графік має перевагу в тому, що чітко показує закономірність взаємодії. Його недоліком є те, що він не передає розподільну інформацію, що міститься в коробкових ділянках.
Приклад з взаємодією
Наступний приклад був представлений у розділі, присвяченому конкретним порівнянням між засобами. Тут також актуально.
У цьому прикладі використовуються вигадані дані з гіпотетичного експерименту, показаного в табл\(\PageIndex{4}\). Дванадцять суб'єктів були обрані з населення суб'єктів високої самооцінки, а додаткові\(12\) суб'єкти були обрані з населення суб'єктів з низькою самооцінкою. Суб'єкти потім виконували завдання і (незалежно від того, наскільки добре вони дійсно зробили) половині в кожній категорії поваги сказали, що вони досягли успіху, а іншій половині сказали, що вони не змогли. Тому було шість предметів у кожній з чотирьох комбінацій шану/результат та\(24\) предметів у всіх.
Після виконання завдання суб'єктам було запропоновано оцінити (за\(10\) -бальною шкалою), скільки їх результату (успіх чи невдача) вони приписують собі, а не через характер завдання.
| Повага | |||
|---|---|---|---|
| Високі | Низький | ||
| Результат | Успіх | 7 | 6 |
| 8 | 5 | ||
| 7 | 7 | ||
| 8 | 4 | ||
| 9 | 5 | ||
| 5 | 6 | ||
| Невдача | 4 | 9 | |
| 6 | 8 | ||
| 5 | 9 | ||
| 4 | 8 | ||
| 7 | 7 | ||
| 3 | 6 | ||
Зведена таблиця ANOVA для цих даних наведена в табл\(\PageIndex{5}\).
| Джерело | дф | SSQ | МС | F | р |
|---|---|---|---|---|---|
| Результат | 1 | 0.0417 | 0.0417 | 0.0256 | 0.8744 |
| Повага | 1 | 2.0417 | 2.0417 | 1,2564 | 0,2756 |
| О х Е | 1 | 35.0417 | 35.0417 | 21.5641 | 0.0002 |
| Помилка | 20 | 32.5000 | 1 6250 | ||
| Всього | 23 | 69.6250 |
Як бачите, єдиним значним ефектом є\(Outcome \times Esteem\) (\(O \times E\)) взаємодія. Форму взаємодії можна побачити на малюнку\(\PageIndex{5}\).
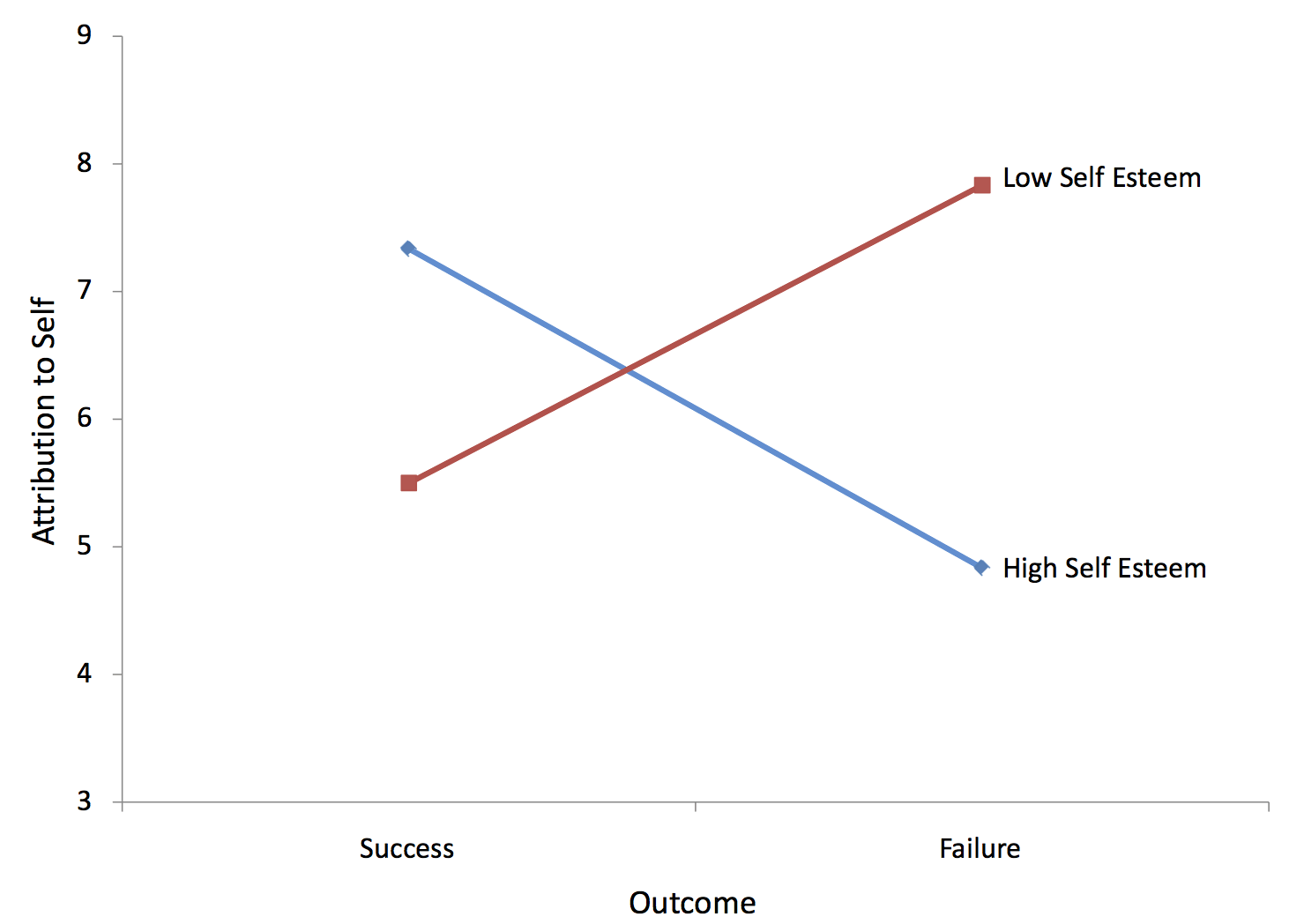
Очевидно, що ефект «Результат» відрізняється для двох рівнів «Поваги»: Для суб'єктів з високою самооцінкою невдача призвела до меншої атрибуції до себе, ніж успіх. На відміну від цього, для суб'єктів з низькою самооцінкою невдача призвела до більшої атрибуції до себе, ніж до успіху. Зверніть увагу, що дві лінії на графіку не паралельні. Непаралельні лінії вказують на взаємодію. Тест на значущість взаємодії визначає, чи виправдано висновок, що лінії в популяції не паралельні. Лінії не повинні перетинатися, щоб там була взаємодія.
Трифакторні конструкції
Трифакторні конструкції аналізуються приблизно так само, як і двофакторні конструкції. Таблиця\(\PageIndex{6}\) показує аналіз дослідження, описаного Франкліном і Кулі, досліджуючи три фактори на силу промислових вентиляторів:
- Форма отвору (шестигранна або кругла)
- Метод збірки (Staked або Spun), і
- Поверхня стовбура (накатана або гладка).
Залежна змінна, що розриває крутний момент, вимірювалася в фут-фунтах. У кожній з восьми комбінацій трьох факторів було вісім спостережень.
Як ви можете бачити в таблиці\(\PageIndex{6}\), є три основні ефекти, три двосторонні взаємодії та одна тристороння взаємодія. Ступені свободи для основних ефектів, як і в двухфакторной конструкції, рівні кількості рівнів фактора мінус один. Оскільки всі фактори тут мають два рівні, всі основні ефекти мають один ступінь свободи. Ступінь свободи взаємодії завжди дорівнює добутку ступенів свободи складових частин. Це стосується трифакторної взаємодії, а також для двофакторних взаємодій. Ступінь похибки свободи дорівнює числу спостережень (\(64\)) мінус кількість груп (\(8\)) і дорівнює\(56\).
| Джерело | дф | SSQ | МС | F | р |
|---|---|---|---|---|---|
| Отвір | 1 | 8258.27 | 8258.27 | 266.68 | <0,0001 |
| Асамблея | 1 | 13369.14 | 13369.14 | 431.73 | <0,0001 |
| В х А | 1 | 2848.89 | 2848.89 | 92.00 | <0,0001 |
| Бочка | 1 | 35.0417 | 35.0417 | 21.5641 | <0,0001 |
| В х В | 1 | 594.14 | 594.14 | 19.1865 | <0,0001 |
| А х В | 1 | 135.14 | 135.14 | 4.36 | 0.0413 |
| В х А х В | 1 | 1396.89 | 1396.89 | 45.11 | <0,0001 |
| Помилка | 56 | 1734.12 | 30.97 | ||
| Всього | 63 | 22 1386.91 |
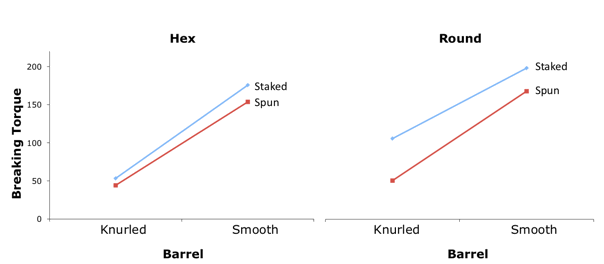
Тристороння взаємодія означає, що двосторонні взаємодії відрізняються залежно від рівня третьої змінної. Звичайним способом зобразити тристоронню взаємодію є побудова двосторонніх взаємодій окремо. \(\PageIndex{6}\)На малюнку показано\(\text{Barrel (Knurled or Smooth)} \times \text{Assembly (Staked or Spun)}\) окремо для двох рівнів форми отвору (Hex або Round). Для Hex Shape дуже мало взаємодії з лініями, близькими до паралельних, з дуже незначною тенденцією до того, що ефект Barrel буде більшим для Staked, ніж для Spun. Двостороння взаємодія для круглої форми відрізняється: ефект Barrel більший для Spun, ніж для Staked. Знаходження значної тристоронньої взаємодії вказує на те, що ця різниця в двосторонніх взаємодіях є значною.
Форматування даних для комп'ютерного аналізу
Дані в таблиці\(\PageIndex{4}\) були переформатовані в таблицю\(\PageIndex{7}\). Зверніть увагу, як є один стовпець для позначення рівня результату і один стовпець для позначення рівня поваги. Кодування виглядає наступним чином:
Висока самооцінка:\(1\)
Низька самооцінка:\(2\)
Успіх:\(1\)
Невдача:\(2\)
| результат | шанувати | атрибут |
|---|---|---|
| 1 | 1 | 7 |
| 1 | 1 | 8 |
| 1 | 1 | 7 |
| 1 | 1 | 8 |
| 1 | 1 | 9 |
| 1 | 1 | 5 |
| 1 | 2 | 6 |
| 1 | 2 | 5 |
| 1 | 2 | 7 |
| 1 | 2 | 4 |
| 1 | 2 | 5 |
| 1 | 2 | 6 |
| 2 | 1 | 4 |
| 2 | 1 | 6 |
| 2 | 1 | 5 |
| 2 | 1 | 4 |
| 2 | 1 | 7 |
| 2 | 1 | 3 |
| 2 | 2 | 9 |
| 2 | 2 | 8 |
| 2 | 2 | 9 |
| 2 | 2 | 8 |
| 2 | 2 | 7 |
| 2 | 2 | 6 |
Щоб використовувати Analysis Lab для виконання розрахунків, ви повинні скопіювати дані, а потім
- Натисніть кнопку «Ввести/Змінити дані». (Можливо, вас попереджають, що з міркувань безпеки ви повинні використовувати комбінацію клавіш для вставки даних.)
- Вставте свої дані.
- Натисніть «Прийняти дані».
- Натисніть кнопку «Додатково» поруч з кнопкою «ANOVA».
- Виберіть «attrib» як залежну змінну і обидва «результат» і «повагу» як змінні «група».
- Натисніть кнопку «Зробити ANOVA».
