15.6: Нерівні розміри вибірки
- Page ID
- 98182
Цілі навчання
- Створюйте, чому нерівність\(n\) може бути проблемою
- Визначте заплутаність
- Обчислення зважених і незважених засобів
- Розрізняють суми квадратів типу I та III типу
- Опишіть, чому причина нерівних розмірів вибірки має значення в тлумаченні
Проблема плутанини
Будь то за конструкцією, випадковістю чи необхідністю, кількість предметів у кожній з умов експерименту може бути не рівною. Наприклад, розміри вибірки для тематичного дослідження «Упередженість проти партнерів ожиріння» наведені в табл\(\PageIndex{1}\). Хоча розміри вибірки були приблизно рівними, умова «Знайомство Типове» мала більшість суб'єктів. Оскільки\(n\) використовується для позначення розміру вибірки окремої групи, то конструкції з неоднаковими розмірами вибірки іноді називають конструкціями з неоднаковими\(n\).
| Вага компаньйона | |||
|---|---|---|---|
| Ожиріння | Типовий | ||
| Відносини | Подруга | 40 | 42 |
| Знайомство | 40 | 54 | |
Ми розглядаємо абсурдну конструкцію, щоб проілюструвати головну проблему, спричинену нерівністю\(n\). Припустимо, експериментатора зацікавило вплив дієти і фізичних вправ на холестерин. Розміри вибірки наведені в табл\(\PageIndex{2}\).
| Вправа | |||
|---|---|---|---|
| Помірний | Жоден | ||
| Дієта | З низьким вмістом жиру | 5 | 0 |
| З високим вмістом жиру | 0 | 5 | |
Те, що робить цей приклад абсурдним, полягає в тому, що немає суб'єктів ні в стані «Низьким вмістом жиру без фізичних вправ», ні в стані «Високий жир помірних вправ». Гіпотетичні дані, що показують зміну холестерину, наведені в табл\(\PageIndex{3}\).
| Вправа | ||||
|---|---|---|---|---|
| Помірний | Жоден | Середнє | ||
| Дієта | З низьким вмістом жиру | -20 | -25 | |
| -25 | ||||
| -30 | ||||
| -35 | ||||
| -15 | ||||
| З високим вмістом жиру | -20 | -5 | ||
| 6 | ||||
| -10 | ||||
| -6 | ||||
| 5 | ||||
| Середнє | -25 | -5 | -15 | |
Останній стовпець показує середню зміну холестерину для двох умов дієти, тоді як останній рядок показує середню зміну холестерину для двох умов фізичних вправ. Значення\(-15\) в нижній правій клітині таблиці є середнім значенням всіх суб'єктів.
З останньої колонки ми бачимо, що ті, хто на дієті з низьким вмістом жиру знижував рівень холестерину в середньому на\(25\) одиниці, тоді як ті, хто на дієті з високим вмістом жирів знижував їх лише на середні\(5\) одиниці. Однак немає ніякого способу дізнатися, чи різниця пов'язана з дієтою або фізичними вправами, оскільки кожен предмет у стані з низьким вмістом жиру був у стані помірних фізичних вправ, і кожен суб'єкт у стані з високим вмістом жиру був у стані без фізичних вправ. Тому дієта і фізичні вправи повністю заплутані. Проблема з нерівністю полягає в\(n\) тому, що це викликає плутанину.
Зважені і невагомі засоби
Різниця між зваженими та незваженими засобами є різницею, вирішальною для розуміння того, як боротися з заплутаним, що виникає внаслідок нерівності\(n\).
Зважені і незважені засоби будуть пояснюватися за допомогою даних, наведених в табл\(\PageIndex{4}\). Тут дієта та фізичні вправи плутаються через\(80\%\) суб'єктів у стані з низьким вмістом жиру, що здійснюються порівняно з тими, хто\(20\%\) перебуває у стані з високим вмістом жиру. Однак не існує повної плутанини, як це було з даними в табл\(\PageIndex{3}\).
Середньозважене значення для «низького жиру» обчислюється як середнє значення «Низького жиру помірних вправ» і середнього значення «Низьким вмістом жиру без фізичних вправ», зважених відповідно до розміру вибірки. Щоб обчислити середнє зваження, ви множите кожне середнє значення на його розмір вибірки і ділите на\(N\), загальну кількість спостережень. Оскільки в стані «Низькі Вправи з низьким вмістом жиру» є чотири суб'єкта та один суб'єкт у стані «Низький вміст жиру без фізичних вправ», засоби зважуються факторами\(4\) і,\(1\) як показано нижче, де\(M_W\) є середньозважене.
\[M_W=\frac{(4)(-27.5)+(1)(-20)}{5}=-26\]
Середньозважене для стану з низьким вмістом жиру - це також середнє значення всіх п'яти балів в цьому стані. Таким чином, якщо ви ігноруєте фактор «Вправа», ви неявно обчислюєте зважені засоби.
Незважене середнє для стану з низьким вмістом жиру (\(M_U\)) - це просто середнє значення двох засобів.
\[M_U=\frac{-27.5-20}{2}=-23.75\]
| Вправа | |||||
|---|---|---|---|---|---|
| Помірний | Жоден | Середньозважене | Незважений середній | ||
| Дієта | З низьким вмістом жиру | -20 | -20 | -26 | -23.750 |
| -25 | |||||
| -30 | |||||
| -35 | |||||
| М=-27.5 | М=-20,0 | ||||
| З високим вмістом жиру | -15 | 6 | -4 | -8.125 | |
| -6 | |||||
| 5 | |||||
| -10 | |||||
| М=-15,0 | М=-1,25 | ||||
| Середньозважене | -25 | -5 | |||
| Незважений середній | -21.25 | -10.625 | |||
Одним із способів оцінити основний ефект дієти є порівняння середньозваженого для дієти з низьким вмістом жиру (\(-26\)) з середнім зваженим для дієти з високим вмістом жирів (\(-4\)). Ця різниця\(-22\) називається «ефектом дієти ігнорування фізичних вправ» і вводить в оману, оскільки більшість суб'єктів з низьким вмістом жиру вправлялися, а більшість суб'єктів з високим вмістом жиру не зробили. Однак різниця між незваженими засобами\(-15.625\) (\((-23.750)-(-8.125)\)) не залежить від цього плутанини і тому є кращою мірою основного ефекту. Коротше кажучи, зважені засоби ігнорують ефекти інших змінних (вправа в цьому прикладі) і призводять до плутанини; незважений означає контроль за дією інших змінних і, отже, усуває плутанину.
Програми статистичного аналізу використовують різні терміни для засобів, які обчислюються, контролюючи інші ефекти. SPSS називає їх розрахунковими граничними засобами, тоді як SAS і SAS JMP називають їх найменшими квадратами засобами.
Типи сум квадратів
У розділі про багатофакторну ANOVA зазначено, що при наявності нерівних розмірів вибірки сума квадратів total не дорівнює сумі сум квадратів для всіх інших джерел варіації. Це пов'язано з тим, що змішані суми квадратів не розподіляються ні на яке джерело варіації. Для даних в таблиці\(\PageIndex{4}\) сума квадратів для Дієти дорівнює\(390.625\), сума квадратів для Вправи дорівнює\(180.625\), а сума квадратів, що плутаються між цими двома факторами, є\(819.375\) (обчислення цього значення виходить за рамки цього вступного тексту). У Зведеній таблиці ANOVA\(\PageIndex{5}\), наведеній у таблиці, ця велика частина сум квадратів не розподіляється ні на яке джерело варіації та представляє «відсутні» суми квадратів. Тобто, якщо скласти суми квадратів для дієти,\(D \times E\) вправи та помилки, ви отримаєте\(902.625\). Якщо\(819.375\) до цього значення додати змішану суму квадратів, ви отримаєте загальну суму квадратів\(1722.000\). Коли плутані суми квадратів не розподіляються ні на яке джерело варіації, суми квадратів називаються сумами квадратів типу III. Суми квадратів типу III на сьогоднішній день є найпоширенішими, і якщо суми квадратів інакше не позначені, можна сміливо вважати, що вони є Типом III.
| Джерело | дф | SSQ | МС | F | р |
|---|---|---|---|---|---|
| Дієта | 1 | 390.625 | 390.625 | 7.42 | 0.034 |
| Вправа | 1 | 180.625 | 180.625 | 3.43 | 0,113 |
| Д х Е | 1 | 15.625 | 15.625 | 0,30 | 0.605 |
| Помилка | 6 | 315.750 | 52.625 | ||
| Всього | 9 | 1722.000 |
Коли всі змішані суми квадратів розподіляються на джерела варіації, суми квадратів називаються сумами квадратів типу I. Порядок, в якому розподіляються заплутані суми квадратів, визначається порядком, в якому перераховані ефекти. Перший ефект отримує будь-які суми квадратів, заплутаних між ним і будь-яким іншим ефектом. Друга отримує суми квадратів, заплутаних між ним і наступними ефектами, але не збентежені першим ефектом тощо Суми квадратів типу I наведені в табл\(\PageIndex{6}\). Як бачите, при сумах квадратів типу I сума всіх сум квадратів - це загальна сума квадратів.
| Джерело | дф | SSQ | МС | F | р |
|---|---|---|---|---|---|
| Дієта | 1 | 1210.000 | 1210.000 | 22.99 | 0,003 |
| Вправа | 1 | 180.625 | 180.625 | 3.43 | 0,113 |
| Д х Е | 1 | 15.625 | 15.625 | 0,30 | 0.605 |
| Помилка | 6 | 315.750 | 52.625 | ||
| Всього | 9 | 1722.000 |
У сумах квадратів типу II суми квадратів, плутані між основними ефектами, не розподіляються ні на яке джерело варіації, тоді як суми квадратів, плутані між основними ефектами та взаємодіями, розподіляються на основні ефекти. У нашому прикладі немає плутанини між\(D \times E\) взаємодією і будь-яким з основних ефектів. Тому суми квадратів II типу дорівнюють сумам квадратів типу III.
Який тип сум квадратів використовувати (необов'язково)
Суми квадратів типу I дозволяють розподілити дисперсію між двома основними ефектами на один з основних ефектів. Якщо немає вагомого аргументу щодо того, як слід розподіляти плутану дисперсію (що рідко, якщо коли-небудь буває), суми квадратів типу I не рекомендується.
Немає єдиної думки щодо того, чи слід надавати перевагу суми квадратів типу II або типу III. З одного боку, якщо немає взаємодії, то суми квадратів типу II будуть більш потужними з двох причин:
- дисперсія, що плутається між основним ефектом і взаємодією, правильно віднесена до основного ефекту і
- зважування засобів за розмірами вибірки дає кращі оцінки ефектів.
Щоб скористатися більшою потужністю сум квадратів типу II, деякі припустили, що якщо взаємодія не є значною, то слід використовувати суми квадратів типу II. Максвелл і Ділейні (2003) застерігають, що такий підхід може призвести до помилки типу II при тесті взаємодії. Тобто це могло привести до висновку, що немає взаємодії в населенні, коли воно дійсно є. Це, в свою чергу, збільшить частоту помилок типу I для перевірки основного ефекту. В результаті їх загальна рекомендація полягає у використанні сум квадратів III типу.
Максвелл і Ділейні (2003) визнали, що деякі дослідники вважають за краще суми квадратів типу II, коли є вагомі теоретичні причини підозрювати відсутність взаємодії і значення p набагато вище, ніж типовий\(α\) рівень\(0.05\). Однак цей аргумент використання сум квадратів II типу не зовсім переконливий. Як стверджували Туреччина (1991) та інші, сумнівно, що будь-який ефект, будь то основний ефект чи взаємодія, є саме\(0\) у населення. До речі, Туреччина стверджувала, що роль тестування значущості полягає у визначенні того, чи можна зробити впевнений висновок про напрямок ефекту, а не просто зробити висновок, що ефект не є точно\(0\).
Нарешті, якщо припустити, що взаємодії немає, то слід використовувати модель ANOVA без терміну взаємодії, а не суми квадратів типу II у моделі, яка включає термін взаємодії. (Моделі без умов взаємодії не розглядаються в цій книзі).
Бувають ситуації, в яких суми квадратів II типу виправдані навіть при сильній взаємодії. Це відбувається тому, що гіпотези, перевірені сумами квадратів II та типу III, різні, і вибір, який використовувати, слід керуватися тим, яка гіпотеза цікавить. Нагадаємо, що суми квадратів типу II вагові клітини засновані на їх розмірах вибірки, тоді як суми квадратів типу III важать всі клітинки однаково. Розглянемо Малюнок\(\PageIndex{1}\), який показує дані з гіпотетичного\(A(2) \times B(2)\) дизайну. Розміри вибірки показані чисельно і зображені графічно областями кінцевих точок.
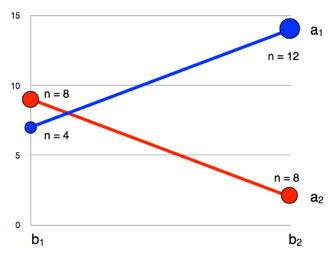
Для початку розглянемо гіпотезу для основного ефекту\(B\) перевірених Типом III сум квадратів. Суми квадратів типу III однаково важать середні і, для цих даних,\(b_2\) граничні середні для\(b_1\) і рівні:
Для\(b_1:(b_1a_1 + b_1a_2)/2 = (7 + 9)/2 = 8\)
Для\(b_2:(b_2a_1 + b_2a_2)/2 = (14+2)/2 = 8\)
Таким чином, немає основного ефекту\(B\) при тестуванні з використанням сум квадратів типу III. Для сум квадратів типу II середні зважуються за розміром вибірки.
Для\(b_1: (4 \times b_1a_1 + 8 \times b_1a_2)/12 = (4 \times 7 + 8 \times 9)/12 = 8.33\)
Для\(b_2: (12 \times b_2a_1 + 8 \times b_2a_2)/20 = (12 \times 14 + 8 \times 2)/20 = 9.2\)
Оскільки середньозважене\(b_2\) граничне значення для більше, ніж середньозважене\(b_1\) граничне для, є основний ефект\(B\) при випробуванні з використанням сум квадратів II типу.
Аналіз типу II та III типу перевіряє різні гіпотези. Спочатку розглянемо випадок, коли відмінності в розмірах вибірки виникають через те, що при вибірці інтактних груп розміри клітин вибірки відображають розміри клітин популяції (принаймні приблизно). При цьому має сенс зважити одні засоби більше, ніж інші і зробити висновок, що є основний ефект\(B\). Це результат, отриманий з сумами квадратів II типу. Однак, якщо відмінності розміру вибірки виникли внаслідок випадкового присвоєння, і в одних клітиках просто траплялося більше спостережень, ніж в інших, то хотілося б оцінити, якими були б основні ефекти при рівних розмірах вибірки і, отже, однаково важити засоби. При однаково зважених середніх значеннях немає основного ефекту\(B\), отриманий результат із сумами квадратів III типу.
Незважений аналіз засобів
Суми квадратів типу III - це випробування відмінностей в незважених середніх. Однак існує альтернативний метод тестування тих же гіпотез, перевірених за допомогою сум квадратів III типу. Цей метод, незважений аналіз засобів, обчислювально-простіший, ніж стандартний метод, але є приблизним тестом, а не точним тестом. Це, однак, дуже гарне наближення у всіх, крім крайніх випадків. Більш того, він точно такий же, як і традиційний тест на ефекти з одним ступенем свободи. Аналітична лабораторія використовує незважений аналіз засобів і тому може не відповідати результатам інших комп'ютерних програм саме тоді, коли є нерівні n, а df більше одиниці.
Причини нерівних розмірів вибірки
Жоден із методів боротьби з неоднаковими розмірами зразків не є дійсним, якщо експериментальна обробка є джерелом нерівних розмірів вибірки. Уявіть собі експеримент, який прагне визначити, чи публічно виконання незручного вчинку вплине на тривогу щодо публічних виступів. У цьому уявному експерименті експериментальну групу просять розкрити групі людей найнезручніше, що вони коли-небудь робили. Контрольну групу просять описати, що вони мали під час останнього прийому їжі. Двадцять суб'єктів набираються для експерименту і випадковим чином діляться на дві рівні групи\(10\), один для експериментального лікування і один для контролю. Слідуючи їх опису, суб'єктам дається опитування ставлення до публічних виступів. Це здається дійсним експериментальним дизайном. Однак з\(10\) випробовуваних в експериментальній групі четверо знялися з експерименту, оскільки не хотіли публічно описувати незручну ситуацію. Ніхто з суб'єктів в контрольній групі не вилучився. Навіть якби аналіз даних показав значний ефект, було б недійсним зробити висновок, що лікування мало ефект, оскільки не можна виключити ймовірне альтернативне пояснення; а саме суб'єкти, які були готові описати незручну ситуацію, відрізнялися від тих, хто цього не був. Таким чином, диференціальний показник відсіву знищив випадкове привласнення суб'єктів до умов, що є критичною особливістю експериментальної конструкції. Жодна сума статистичного коригування не може компенсувати цей недолік.
- Максвелл, С.Е., & Delaney, HD (2003) Проектування експериментів та аналіз даних: перспектива порівняння моделей, друге видання, Лоуренс Ерлбаум Associates, Mahwah, Нью-Джерсі.
- Туреччина, Дж. (1991) Філософія множинних порівнянь, Статистична наука, 6, 110-116.
