15.3: Однофакторна ANOVA
- Page ID
- 98176
Цілі навчання
- Створіть, що оцінює середній квадрат між (\(MSB\)), коли нульова гіпотеза істинна і коли нульова гіпотеза помилкова
- Обчислити\(MSE\)
- Обчислення\(F\) та два його параметри ступеня свободи
- Поясніть, чому ANOVA найкраще розглядається як тест з двома хвостами, хоча буквально використовується лише один хвіст дистрибутива
- Розділення сум квадратів на умову та помилку
- Форматування даних для використання з програмою комп'ютерної статистики
У цьому розділі показано, як ANOVA можна використовувати для аналізу однофакторного дизайну між предметами. В якості основного прикладу ми будемо використовувати тематичне дослідження «Усмішки та поблажливість». У цьому дослідженні було чотири умови з\(34\) суб'єктами в кожному стані. Був один бал на предмет. Нульова гіпотеза, перевірена ANOVA, полягає в тому, що засоби популяції для всіх умов однакові. Це може виражатися наступним чином:
\[H_0: \mu _1 = \mu _2 = ... = \mu _k\]
де\(H_0\) нульова гіпотеза і\(k\) - кількість умов. У дослідженні «Усмішки та поблажливість» нульова гіпотеза\(k = 4\)
\[H_0: \mu _{false} = \mu _{felt} = \mu _{miserable} = \mu _{neutral}\]
Якщо нульова гіпотеза відхилена, то можна зробити висновок, що хоча б одне з засобів населення відрізняється хоча б від одного іншого середнього популяції.
Аналіз дисперсії - це метод перевірки відмінностей між засобами шляхом аналізу дисперсії. Тест заснований на двох оцінках дисперсії популяції (\(\sigma ^2\)). Одна оцінка називається середньою квадратною похибкою (\(MSE\)) і базується на відмінностях між балами всередині груп. \(MSE\)оцінює\(\sigma ^2\) незалежно від того, чи вірна нульова гіпотеза (засоби популяції рівні). Друга оцінка називається середнім квадратом між (\(MSB\)) і заснована на відмінностях між вибірковими засобами. \(MSB\)оцінює лише в тому\(\sigma ^2\) випадку, якщо кошти населення рівні. Якщо кошти населення не рівні, то\(MSB\) оцінює кількість більше, ніж\(\sigma ^2\). Тому якщо\(MSB\) набагато більше, ніж на\(MSE\), то кошти населення навряд чи будуть рівні. З іншого боку, якщо приблизно те ж саме\(MSE\), то дані узгоджуються з нульовою гіпотезою про те, що засоби популяції рівні.\(MSB\)
Перш ніж приступити до розрахунку\(MSE\) і\(MSB\), важливо врахувати припущення, зроблені ANOVA:
- Популяції мають однакову дисперсію. Це припущення називається припущенням\(\textit{homogeneity of variance}\).
- Популяції в нормі розподілені.
- Кожне значення відбирається незалежно один від одного значення. Це припущення вимагає, щоб кожен суб'єкт надавав лише одне значення. Якщо суб'єкт надає два бали, то значення не є незалежними. Аналіз даних з двома балами на предмет показаний у розділі, присвяченому темам ANOVA пізніше в цьому розділі.
Ці припущення такі ж, як і для t тесту відмінностей між групами, за винятком того, що вони застосовуються до двох або більше груп, а не тільки до двох груп.
Засоби та відхилення чотирьох груп у прикладі «Посмішки та поблажливість» наведені в табл\(\PageIndex{1}\). Зверніть увагу, що в кожній з чотирьох умов є\(34\) предмети (помилковий, Повстяний, Нещасний і Нейтральний).
| Стан | Середнє | дисперсія |
|---|---|---|
| Помилковий | 5.3676 | 3.380 |
| Повсть | 4.9118 | 2.8253 |
| жалюгідний | 4.9118 | 2.1132 |
| Нейтральний | 4.1176 | 2.3191 |
Розміри вибірки
Перші розрахунки в цьому розділі все припускають, що в кожній групі існує однакова кількість спостережень. Розрахунки нерівних розмірів вибірки наведені тут. Ми будемо посилатися на кількість спостережень у кожній\(n\) групі як і загальну кількість спостережень як\(N\). За цими даними існує чотири групи\(34\) спостережень. Тому\(n = 34\) і\(N = 136\).
Обчислення MSE
Нагадаємо, що припущення однорідності дисперсії стверджує, що дисперсія всередині кожної з популяцій (\(\sigma ^2\)) однакова. Ця дисперсія - це величина\(\sigma ^2\), оцінена\(MSE\) і обчислюється як середнє значення відхилень вибірки. Для цих даних\(MSE\) значення дорівнює\(2.6489\).
Обчислення MSB
Формула для\(MSB\) заснована на тому, що дисперсія розподілу вибірки середнього
\[\sigma _{M}^{2}=\frac{\sigma ^2}{n}\]
де\(n\) - розмір вибірки кожної групи. Переставляючи цю формулу, ми маємо
\[\sigma ^2=n\sigma _{M}^{2}\]
Тому, якби ми знали дисперсію розподілу вибірки середнього, ми могли б обчислити,\(\sigma ^2\) помноживши її на\(n\). Хоча ми не знаємо дисперсії розподілу вибірки середнього, ми можемо оцінити її з дисперсією засобів вибірки. Для даних поблажливості дисперсія чотирьох вибіркових засобів становить\(0.270\). Для оцінки\(\sigma ^2\) множимо дисперсію вибіркового засобу (\(0.270\)) на\(n\) (кількість спостережень в кожній групі, яка є\(34\)). Ми знаходимо це\(MSB = 9.179\).
Підсумовуємо наступні кроки:
- Обчислити кошти.
- Обчислити дисперсію засобів.
- Помножте дисперсію засобів на\(n\).
Резюме
Якщо засоби населення рівні, то обидва\(MSE\) і\(MSB\) є оцінками\(\sigma ^2\) і тому повинні бути приблизно однаковими. Природно, вони не будуть точно однаковими, оскільки вони є лише оцінками і базуються на різних аспектах даних:\(MSB\) обчислюється з вибіркових засобів, а\(MSE\) обчислюється з відхилень вибірки.
Якщо кошти населення не рівні, то все одно\(MSE\) оцінюватимуть,\(\sigma ^2\) оскільки відмінності в чисельності населення не впливають на розбіжності. Однак відмінності в засобах популяції впливають,\(MSB\) оскільки відмінності між засобами населення пов'язані з відмінностями між вибірковими засобами. Звідси випливає, що чим більше відмінності між вибірковими засобами, тим більше\(MSB\).
Примітка
Коротше кажучи,\(MSE\) оцінює,\(\sigma ^2\) чи рівні засоби населення, тоді як\(MSB\) оцінки\(\sigma ^2\) лише тоді, коли засоби населення рівні, і оцінює більшу кількість, коли вони не рівні.
Порівняння MSE та MSB
Критичним кроком в ANOVA є порівняння\(MSE\) і\(MSB\). Оскільки\(MSB\) оцінює більшу кількість, ніж\(MSE\) лише тоді, коли кошти населення не рівні, знахідка більшого,\(MSB\) ніж a,\(MSE\) є ознакою того, що засоби населення не рівні. Але оскільки\(MSB\) може бути більше, ніж\(MSE\) випадково, навіть якщо засоби населення рівні,\(MSB\) повинні бути набагато більшими, ніж для\(MSE\) того, щоб виправдати висновок, що засоби населення відрізняються. Але скільки більше повинно\(MSB\) бути? Для даних «Посмішки і поблажливість»,\(MSB\) і\(MSE\) є\(9.179\) і\(2.649\), відповідно. Чи є ця різниця досить велика? Щоб відповісти, нам потрібно було б знати ймовірність того, що велика різниця або більша різниця, якби засоби населення були рівними. Математику, необхідну для відповіді на це питання, опрацьовував статистик Р.Фішер. Хоча оригінальна рецептура Фішера прийняла дещо іншу форму, стандартний метод визначення ймовірності заснований на співвідношенні\(MSB\) до\(MSE\). Це співвідношення названо на честь Фішера і називається\(F\) співвідношенням.
Для цих даних\(F\) співвідношення дорівнює
\[F = \frac{9.179}{2.649} = 3.465\]
Тому в\(3.465\) рази\(MSB\) вище, ніж\(MSE\). Чи могло б це статися, якби всі засоби населення були рівними? Це залежить від розміру вибірки. Маючи невеликий розмір вибірки, це не було б занадто дивно, оскільки результати невеликих зразків нестабільні. Однак при дуже великій вибірці\(MSB\) і\(MSE\) майже завжди приблизно однакові, і\(F\) співвідношення\(3.465\) або більше було б дуже незвично. \(\PageIndex{1}\)На малюнку показано розподіл вибірки\(F\) для розміру вибірки в дослідженні «Посмішки та поблажливість». Як бачите, він має позитивний перекіс.
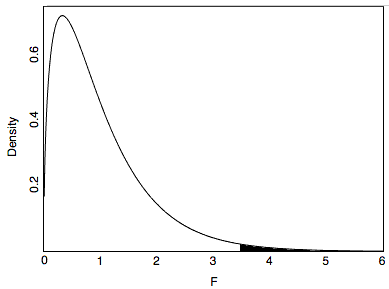
З\(\PageIndex{1}\) малюнка ви можете бачити, що\(F\) співвідношення\(3.465\) або вище є незвичайними явищами. Площа праворуч від\(3.465\) представляє ймовірність\(F\) того, що великий або більший і дорівнює\(0.018\). Іншими словами, враховуючи нульову гіпотезу, що всі засоби популяції рівні, значення ймовірності є,\(0.018\) і тому нульова гіпотеза може бути відхилена. Висновок про те, що хоча б одне з засобів населення відрізняється хоча б від одного з інших, виправданий.
Форма\(F\) розподілу залежить від розміру вибірки. Точніше, він залежить від двох параметрів ступеня свободи (\(df\)): один для чисельника (\(MSB\)) і один для знаменника (\(MSE\)). Нагадаємо, що ступені свободи для оцінки дисперсії дорівнюють числу спостережень мінус одиниця. Так як\(MSB\) це дисперсія\(k\) засобів, вона має\(k - 1\)\(df\). The\(MSE\) є середнім\(k\) показником відхилень, кожен з\(n - 1\)\(df\). Тому\(df\) для\(MSE\) є\(k(n - 1) = N - k\), де\(N\) загальна кількість спостережень,\(n\) це кількість спостережень в кожній групі, і\(k\) це кількість груп. Підсумовуємо:
\[df_{numerator} = k-1\]
\[df_{denominator} = N-k\]
Для даних «Посмішки та поблажливість»,
\[df_{numerator} = k-1=4-1=3\]
\[df_{denominator} = N-k=136-4=132\]
\(F = 3.465\)
Калькулятор\(F\) розподілу показує, що\(p = 0.018\).
F Калькулятор
Однохвостий або два?
Чи є значення ймовірності з\(F\) коефіцієнта однохвостою або двоххвостою ймовірністю? У буквальному сенсі це однохвоста ймовірність, оскільки, як ви бачите на малюнку\(\PageIndex{1}\), ймовірність - це область в правому хвості розподілу. Однак\(F\) співвідношення чутливе до будь-якої закономірності відмінностей між засобами. Отже, це тест двоххвостої гіпотези і найкраще вважається двоххвостим тестом.
Відносини до\(t\) тесту
Оскільки тест ANOVA та незалежних груп можуть\(t\) перевірити різницю між двома засобами, вам може бути цікаво, який з них використовувати. На щастя, це не має значення, оскільки результати завжди будуть однаковими. Коли існує лише дві групи, такі відносини між\(F\) і завжди\(t\) будуть триматися:
\[F(1,dfd) = t^2(df)\]
де\(dfd\) - ступені свободи для знаменника\(F\) тесту і\(df\) - ступені свободи для\(t\) тесту. \(dfd\)завжди буде рівним\(df\).
Джерела варіації
Чому бали в експерименті відрізняються один від одного? Розглянемо оцінки двох предметів у дослідженні «Усмішки та поблажливість»: один із стану «Помилкова посмішка» та один із стану «Посмішка відчувається». Очевидною можливою причиною того, що бали могли відрізнятися, є те, що до випробуваних ставилися по-різному (вони були в різних умовах і бачили різні подразники). Друга причина полягає в тому, що обидва суб'єкти, можливо, відрізнялися щодо своєї схильності поблажливо судити людей. Третя полягає в тому, що, можливо, один з випробовуваних був у поганому настрої після отримання низької оцінки на тесті. Ви можете собі уявити, що існує безліч інших причин, чому оцінки двох предметів можуть відрізнятися. Усі ці причини, крім першої (суб'єкти трактувалися по-різному) - це можливості, які не перебували під експериментальним дослідженням, і, отже, всі відмінності (варіації) через ці можливості незрозумілі. Традиційно називати незрозумілу помилку дисперсії, хоча немає ніякого натяку на те, що була допущена помилка. Тому варіацію в цьому експерименті можна вважати або варіацією через стан, в якому перебував суб'єкт, або через помилку (загальна сума всіх причин оцінки суб'єктів може відрізнятися, які не були виміряні).
Однією з важливих характеристик ANOVA є те, що вона розділяє варіацію на різні її джерела. У ANOVA термін сума квадратів (\(SSQ\)) використовується для позначення варіації. Загальна варіація визначається як сума квадратних відмінностей між кожним балом та середнім значенням усіх предметів. Середнє значення всіх суб'єктів називається великим середнім і позначається як ГМ. (Коли в кожній умові однакова кількість суб'єктів, велике середнє - це середнє значення умови означає.) Загальна сума квадратів визначається як
\[SSQ_{total}=\sum (X-GM)^2\]
що означає взяти кожен бал, відняти від нього велике середнє, квадрат різниці, а потім підсумувати ці квадратні значення. Для дослідження «Усмішки та поблажливість»,\(SSQ_{total}=377.19\).
Умова суми квадратів обчислюється, як показано нижче.
\[SSQ_{condition}=n\left [ (M_1-GM)^2 + (M_2-GM)^2 + \cdots +(M_k-GM)^2 \right ]\]
де\(n\) - кількість балів в кожній групі,\(k\) це кількість груп,\(M_1\) це середнє значення для\(\text{Condition 1}\),\(M_2\) є середнім для\(\text{Condition 2}\), і\(M_k\) є середнім для\(\text{Condition k}\). Для дослідження «Посмішки та поблажливість» цінностями є:
\[\begin{align*} SSQ_{condition} &= 34\left [ (5.37-4.83)^2 + (4.91-4.83)^2 + (4.91-4.83)^2 + (4.12-4.83)^2\right ]\\ &= 27.5 \end{align*}\]
Якщо є нерівні розміри вибірки, то єдина зміна полягає в тому, що для умови суми квадратів використовується наступна формула:
\[SSQ_{condition}=n_1(M_1-GM)^2 + n_2(M_2-GM)^2 + \cdots + n_k(M_k-GM)^2\]
де\(n_i\) - розмір вибірки\(i^{th}\) умови. \(SSQ_{total}\)обчислюється так само, як показано вище.
Похибка суми квадратів - це сума квадратів відхилень кожного балу від середнього його групового значення. Це можна записати як
\[SSQ_{error}=\sum (X_{i1}-M_1)^2 + \sum (X_{i2}-M_2)^2 + \cdots + \sum (X_{ik}-M_k)^2\]
де\(X_{i1}\)\(i^{th}\) оцінка в\(\text{group 1}\) і\(M_1\) є середнім для\(\text{group 1}\),\(X_{i2}\) є\(i^{th}\) оцінка в\(\text{group 2}\) і\(M_2\) є середнім для і\(\text{group 2}\) т.д. для дослідження «Посмішки і поблажливість», засоби є:\(5.368\),\(4.912\),\(4.912\), і \(4.118\). Отже\(SSQ_{error}\), це:
\[\begin{align*} SSQ_{error} &= (2.5-5.368)^2 + (5.5-5.368)^2 + ... + (6.5-4.118)^2\\ &= 349.65 \end{align*}\]
Похибка суми квадратів також може бути обчислена відніманням:
\[SSQ_{error} = SSQ_{total} - SSQ_{condition}\]
\[\begin{align*} SSQ_{error} &= 377.189 - 27.535\\ &= 349.65 \end{align*}\]
Тому загальну суму квадратів\(377.19\) можна розділити на\(SSQ_{condition}(27.53)\) і\(SSQ_{error} (349.66)\).
Після обчислення сум квадратів середні квадрати (\(MSB\)і\(MSE\)) можна легко обчислити. Формули такі:
\[MSB = \frac{SSQ_{condition}}{dfn}\]
де\(dfn\) - чисельник ступенів свободи і дорівнює\(k - 1 = 3\).
\[MSB = \frac{27.535}{3}=9.18\]
яке є тим самим значенням\(MSB\) отриманого раніше (за винятком похибки округлення). Аналогічно,
\[MSE = \frac{SSQ_{error}}{dfd}\]
де\(dfd\) - ступені свободи для знаменника і дорівнює\(N - k\).
\(dfd = 136 - 4 = 132\)
\(MSE = 349.66/132 = 2.65\)
який такий же, як отриманий раніше (за винятком помилки округлення). Зверніть увагу, що часто\(dfd\) називають помилкою\(dfe\) для ступенів свободи.
Аналіз дисперсії Зведена таблиця, показана нижче, є зручним способом узагальнити поділ дисперсії. Помилки округлення були виправлені.
| Джерело | дф | SSQ | МС | F | р |
|---|---|---|---|---|---|
| Стан | 3 | 27.5349 | 9.1783 | 3.465 | 0.0182 |
| Помилка | 132 | 349,6544 | 2.6489 | ||
| Всього | 135 | 377.1893 |
Перший стовпець показує джерела варіації, другий стовпець показує ступені свободи, третій показує суми квадратів, четвертий показує середні квадрати, п'ятий показує\(F\) співвідношення, а останній показує значення ймовірності. Зверніть увагу, що середні квадрати - це завжди суми квадратів, поділені на ступені свободи. \(F\)І\(p\) мають відношення тільки до Умови. Хоча середня квадратна сума може бути обчислена шляхом ділення суми квадратів на ступені свободи, вона, як правило, не представляє особливого інтересу і тут опускається.
Форматування даних для комп'ютерного аналізу
Більшість комп'ютерних програм, які обчислюють ANOVA, вимагають, щоб ваші дані були в певній формі. Розглянемо дані в табл\(\PageIndex{3}\).
| Група 1 | Група 2 | Група 3 |
|---|---|---|
| 3 | 2 | 8 |
| 4 | 4 | 5 |
| 5 | 6 | 5 |
Тут є три групи, кожна з яких має три спостереження. Щоб відформатувати ці дані для комп'ютерної програми, зазвичай потрібно використовувати дві змінні: перша вказує групу, в якій знаходиться суб'єкт, а друга - сама оцінка. Переформатований варіант даних у таблиці\(\PageIndex{3}\) наведено в табл\(\PageIndex{4}\).
| Г | У |
|---|---|
| 1 | 3 |
| 1 | 4 |
| 1 | 5 |
| 2 | 2 |
| 2 | 4 |
| 2 | 6 |
| 3 | 8 |
| 3 | 5 |
| 3 | 5 |
Щоб використовувати Analysis Lab для виконання розрахунків, ви повинні скопіювати дані, а потім
- Натисніть кнопку «Ввести/Змінити дані». (Можливо, вас попереджають, що з міркувань безпеки ви повинні використовувати комбінацію клавіш для вставки даних.)
- Вставте свої дані.
- Натисніть «Прийняти дані».
- Встановіть залежну змінну в значення\(Y\).
- Встановіть для змінної групування значення\(G\).
- Натисніть кнопку ANOVA.
Ви знайдете, що\(F = 1.5\) і\(p = 0.296\).
