13.2: Приклад розрахунків

Last updated
Save as PDF

Page ID: 98257

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

навички розвитку

Обчислення потужності за допомогою біноміального розподілу
Обчислення потужності за допомогою звичайного розподілу
Використовуйте калькулятор потужності для обчислення потужності для\(t\) розподілу

У тематичному дослідженні «Струшування та перемішування Мартіні» питання полягало в тому, чи може пан Бонд визначити різницю між мартіні, які перемішували, і мартіні, які були потрясені. Заради цього прикладу припустимо, що він може сказати різницю і здатний правильно заявити, чи був мартіні струшувався або\(0.75\) перемішувався того часу. Тепер, припустимо, проводиться експеримент, щоб дослідити, чи може пан Бонд визначити різницю. Зокрема, чи правильний містер\(0.50\) Бонд більше часу? Ми знаємо, що він є (це припущення на прикладі). Однак експериментатор не знає і просить містера Бонда судити\(16\) Мартіні. Експериментатор зробить тест на значущість на основі біноміального розподілу. Зокрема, якщо один хвостатий тест є значним на\(0.05\) рівні, то він або вона зробить висновок, що містер Бонд може сказати різницю. Значення ймовірності обчислюється за умови, що нульова гіпотеза є true (\(\pi =0.50\)). Тому експериментатор визначить, скільки разів містер Бонд правильний, і обчислить ймовірність бути правильним, що багато або більше разів враховуючи, що нульова гіпотеза вірна. Питання: яка ймовірність того, що експериментатор правильно відкине нульову гіпотезу\(\pi =0.50\)? Іншими словами, в чому сила цього експерименту?

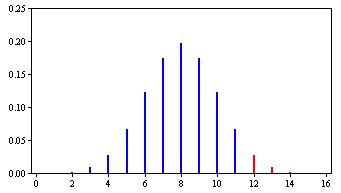
Біноміальний розподіл для\(N = 16\) і\(\pi =0.50\) показано на рис\(\PageIndex{1}\). Імовірність бути правильною на\(11\) або декількох випробуваннях є\(0.105\) і ймовірність бути правильним на\(12\) або більше випробувань є\(0.038\). Тому ймовірність бути правильним на\(12\) або більшій кількості випробувань менше\(0.05\). Це означає, що нульова гіпотеза буде відхилена, якщо містер Бонд буде правильним на\(12\) або декількох випробуваннях і не буде відхилений інакше.

Біноміальний калькулятор

Малюнок\(\PageIndex{1}\): Біноміальний розподіл для\(N = 16\) і\(\pi =0.50\)

Ми знаємо, що містер Бонд має\(0.75\) рацію часу. (Очевидно, що експериментатор цього не знає або не було б необхідності в експерименті.) Біноміальний розподіл з\(N = 16\) і\(\pi =0.75\) показано на рис\(\PageIndex{2}\).

Малюнок\(\PageIndex{2}\): Біноміальний розподіл для\(N = 16\) і\(\pi =0.75\)

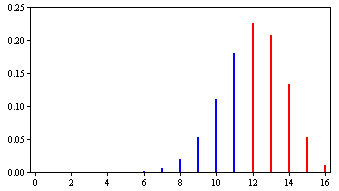
Імовірність бути правильним на\(12\) або декількох випробуваннях є\(0.63\). Тому сила експерименту є\(0.63\).

Підводячи підсумок, ймовірність бути правильною на\(12\) або більше випробуваннях, враховуючи, що нульова гіпотеза істинна, менша ніж\(0.05\). Тому, якщо містер Бонд буде правильним на\(12\) або декількох випробуваннях, нульова гіпотеза буде відхилена. Враховуючи справжню здатність містера Бонда бути правильним на\(0.75\) випробуваннях, ймовірність того, що він буде правильним на\(12\) або декількох випробуваннях є\(0.63\). Тому влада є\(0.63\).

У розділі «Тестування єдиного середнього значення для значущості» перший приклад базувався на припущенні, що експериментатор знав дисперсію популяції. Хоча це рідко буває вірно на практиці, приклад дуже корисний в педагогічних цілях. З цієї ж причини наступний приклад передбачає, що експериментатор знає дисперсію популяції. Калькулятори потужності доступні для ситуацій, в яких експериментатор не знає дисперсії населення.

Припустимо, що тест на досягнення математики, як відомо, має середнє значення\(75\) і стандартне відхилення\(10\). Дослідника цікавить, чи новий метод навчання призводить до більш високого середнього. Припустимо, що хоча експериментатор цього не знає, чисельність населення для нового методу є\(80\). Дослідник планує вибірку\(25\) суб'єктів і зробити однохвостий тест на те, чи є середнє значення зразка значно вище, ніж\(75\). Яка ймовірність того, що дослідник правильно відкине помилкову нульову гіпотезу про те, що сукупність означає для нового методу\(75\) або нижче? Нижче показано, як обчислюється ця ймовірність.

Дослідник припускає, що стандартне відхилення популяції при новому методі таке ж, як і при старому методі (\(10\)) і що розподіл нормальний. Оскільки стандартне відхилення населення вважається відомим, дослідник може використовувати нормальний розподіл, а не розподіл t для обчислення\(p\) значення. Нагадаємо, що стандартна похибка середнього (\(\sigma _M\)) дорівнює

\[\sigma _M=\frac{\sigma }{\sqrt{N}}\]

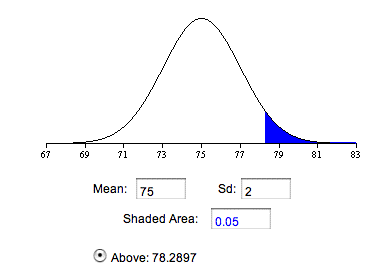
що дорівнює\(10/5 = 2\) в цьому прикладі. Як видно на малюнку\(\PageIndex{3}\), якщо нульова гіпотеза про те, що середнє значення популяції\(75\) дорівнює, є істинною, то ймовірність того, що середнє значення вибірки буде більшим або\(78.29\) рівним є\(0.05\). Тому експериментатор буде відкидати нульову гіпотезу, якщо зразок середнього\(M\),,,\(78.29\) або більше.

Малюнок, створений за допомогою зворотного нормального калькулятора)

Тоді питання полягає в тому, яка ймовірність того, що експериментатор отримує середнє значення вибірки більше, ніж\(78.29\) враховуючи, що середнє значення популяції є\(80\)? Малюнок\(\PageIndex{4}\) показує, що така ймовірність є\(0.80\).

Малюнок, створений за допомогою звичайного калькулятора)

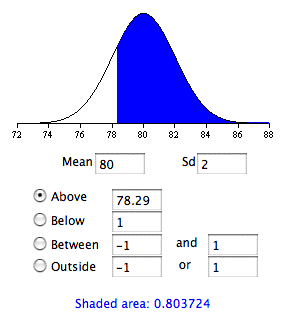
Тому ймовірність того, що експериментатор відкине нульову гіпотезу про те, що середнє населення нового методу\(75\) є\(0.80\). Іншими словами,\(power = 0.80\).

Розрахунок потужності більш складний для\(t\) випробувань і для аналізу дисперсії. Калькулятор потужності обчислює потужність для\(t\) перевірки незалежних груп. Калькулятори для інших типів конструкцій наведені нижче:

Калькулятори потужності Расса Лента