10.7: Довірчий інтервал для середнього
- Page ID
- 98026
Цілі навчання
- Використовуйте зворотний калькулятор нормального розподілу, щоб знайти значення, яке буде\(z\) використано для довільного інтервалу
- Обчислити довірчий інтервал на середньому\(\sigma\), коли відомо
- Визначте, чи використовувати\(t\) дистрибутив або звичайний розподіл
- Обчислити довірчий інтервал на середньому, коли\(\sigma\) оцінюється
Коли ви обчислюєте довірчий інтервал на середньому, ви обчислюєте середнє значення вибірки, щоб оцінити середнє значення сукупності. Зрозуміло, що якби ви вже знали середнє значення населення, не було б необхідності в довірчому інтервалі. Однак, щоб пояснити, як будуються довірчі інтервали, ми будемо працювати назад і почати з припущення особливостей населення. Потім ми покажемо, як вибіркові дані можуть бути використані для побудови довірчого інтервалу.
Припустимо, що ваги дітей\(10\) -річного віку в нормі розподіляються із середнім\(90\) значенням і стандартним відхиленням\(36\). Який розподіл вибірки середнього значення для розміру вибірки\(9\)? Нагадаємо, з розділу про розподіл вибірки означає, що середнє значення розподілу вибірки є\(\mu\) і стандартна похибка середнього значення дорівнює
\[\sigma _M=\frac{\sigma }{\sqrt{N}}\]
Для наданого прикладу розподіл вибірки середнього значення має середнє значення\(90\) і стандартне відхилення\(36/3 = 12\). Зверніть увагу, що стандартне відхилення розподілу вибірки є його стандартною похибкою. На малюнку\(\PageIndex{1}\) показаний цей розподіл. Затінена область являє собою середину\(95\%\) розподілу і тягнеться від\(66.48\) до\(113.52\). Ці межі обчислювалися шляхом додавання і віднімання\(1.96\) стандартних відхилень до/з середнього значення\(90\) наступним чином:
\[90 - (1.96)(12) = 66.48\]
\[ 90 + (1.96)(12) = 113.52\]
Значення\(1.96\) засноване на тому, що\(95\%\) площа нормального розподілу знаходиться в межах\(1.96\) стандартних відхилень від середнього;\(12\) є стандартною похибкою середнього.
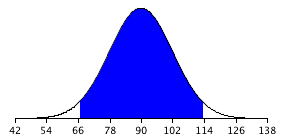
\(\PageIndex{1}\)На малюнку видно, що\(95\%\) з засобів не більше\(23.52\) одиниць (\(1.96\)стандартних відхилень) від середнього значення\(90\). Тепер розглянемо ймовірність того, що середнє значення вибірки, обчислене у випадковій вибірці, знаходиться в межах\(23.52\) одиниць середньої чисельності населення\(90\). Оскільки\(95\%\) розподіл знаходиться в межах\(23.52\), ймовірність того\(90\), що середнє значення з будь-якої даної вибірки буде в межах\(23.52\)\(90\) є\(0.95\). Це означає, що якщо ми неодноразово обчислимо середнє (\(M\)) з вибірки і створимо інтервал від\(M - 23.52\) до\(M + 23.52\), цей інтервал буде містити середнє\(95\%\) значення популяції часу. Загалом, ви обчислюєте\(95\%\) довірчий інтервал для середнього за такою формулою:
\[\text{Lower limit} = M - Z_{0.95}\sigma _M\]
\[\text{Upper limit} = M + Z_{0.95}\sigma _M\]
де\(Z_{0.95}\) - кількість стандартних відхилень, що відходять від середнього нормального розподілу,\(0.95\) необхідного для утримання площі, і\(\sigma _M\) є стандартною похибкою середнього.
Якщо уважно придивитися до цієї формули довірчого інтервалу, то помітите, що вам потрібно знати стандартне відхилення (\(\sigma\)), щоб оцінити середнє значення. Це може здатися нереальним, і це так. Однак обчислення довірчого інтервалу, коли\(\sigma\) відомо, простіше, ніж коли\(\sigma\) потрібно оцінити, і служить педагогічній меті. Пізніше в цьому розділі ми покажемо, як обчислити довірчий інтервал для середнього, коли\(\sigma\) потрібно оцінити.
Припустимо, наступні п'ять чисел були вибрані з нормального розподілу зі стандартним відхиленням\(2.5: 2, 3, 5, 6,\; and\; 9\). Щоб обчислити\(95\%\) довірчий інтервал, почніть з обчислення середньої і стандартної помилки:
\[M = \frac{2 + 3 + 5 + 6 + 9}{5} = 5\]
\[\sigma _M=\frac{2.5}{\sqrt{5}}=1.118\]
\(Z_{0.95}\)можна знайти за допомогою калькулятора нормального розподілу та вказати, що затінена область є\(0.95\) і вказує, що ви хочете, щоб область була між точками зрізу. Як показано на малюнку\(\PageIndex{2}\), значення є\(1.96\). Якби ви хотіли обчислити\(99\%\) довірчий інтервал, ви б встановили затінену область,\(0.99\) і результат був би\(2.58\).
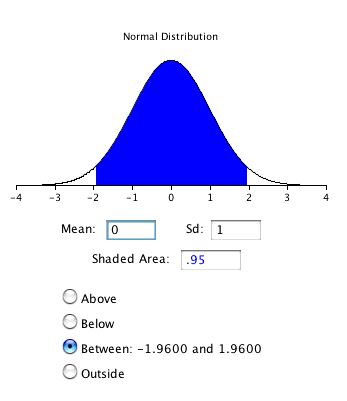
Довірчий інтервал потім можна обчислити наступним чином:
\[\text{Lower limit} = 5 - (1.96)(1.118)= 2.81\]
\[\text{Upper limit} = 5 + (1.96)(1.118)= 7.19\]
Ви повинні використовувати\(t\) розподіл, а не звичайний розподіл, коли дисперсія невідома і повинна бути оцінена за вибірковими даними. Коли розмір вибірки великий, скажімо\(100\) або вище, розподіл t дуже схожий на стандартний нормальний розподіл. Однак при менших розмірах вибірки\(t\) розподіл є лептокуртичним, а це означає, що він має відносно більше балів у хвостах, ніж звичайний розподіл. Як результат, ви повинні продовжити далі від середнього, щоб містити задану частку площі. Нагадаємо, що при нормальному\(95\%\) розподілі розподіл знаходиться в межах\(1.96\) стандартних відхилень від середнього. Використовуючи\(t\) розподіл, якщо у вас є тільки розмір\(95\%\) вибірки\(5\), площа знаходиться в межах\(2.78\) стандартних відхилень від середнього. Тому стандартна похибка середнього значення буде помножена на,\(2.78\) а не\(1.96\).
Значення, які слід\(t\) використовувати в довірчому інтервалі, можна переглянути в таблиці\(t\) розподілу. Невеликий варіант такої таблиці наведено в табл\(\PageIndex{1}\). Перший стовпець,\(df\), позначає ступені свободи, а для довірчих інтервалів на\(df\) середньому, дорівнює\(N\) тому\(N - 1\), де розмір вибірки.
| дф | 0,95 | 0,99 |
|---|---|---|
| 2 | 4.303 | 9.925 |
| 3 | 3.182 | 5.841 |
| 4 | 2.776 | 4.604 |
| 5 | 2.571 | 4.032 |
| 8 | 2.306 | 3.355 |
| 10 | 2.228 | 3.169 |
| 20 | 2.086 | 2.845 |
| 50 | 2.009 | 2.678 |
| 100 | 1,984 | 2.626 |
Ви також можете скористатися калькулятором «зворотного розподілу t», щоб знайти\(t\) значення для використання в довірчих інтервалах. Детальніше про\(t\) дистрибутив ви дізнаєтеся в наступному розділі.
Припустімо, що наступні п'ять чисел вибірки з нормального розподілу:\(2, 3, 5, 6,\; and\; 9\) і що стандартне відхилення невідомо. Першими кроками є обчислення зразка середнього значення та дисперсії:
\[M=5\; \text{and}\; S^2=7.5\]
Наступним кроком буде оцінка стандартної похибки середнього значення. Якби ми знали дисперсію населення, ми могли б використовувати таку формулу:
\[\sigma _M=\frac{\sigma }{\sqrt{N}}\]
Замість цього обчислюємо оцінку стандартної помилки (\(s_M\)):
\[s _M=\frac{s}{\sqrt{N}}=1.225\]
Наступним кроком буде пошук значення\(t\). Як видно з таблиці\(\PageIndex{1}\), значення\(95\%\) інтервалу для\(df = N - 1 = 4\) дорівнює\(2.776\). Довірчий інтервал потім обчислюється так само, як і коли\(\sigma _M\). Єдині відмінності в тому, що\(s_M\) і т,\(\sigma _M\) а не і\(Z\) використовуються.
\[\text{Lower limit} = 5 - (2.776)(1.225) = 1.60\]
\[\text{Upper limit} = 5 + (2.776)(1.225) = 8.40\]
Більш загально формула\(95\%\) довірчого інтервалу на середньому дорівнює:
\[\text{Lower limit} = M - (t_{CL})(s_M)\]
\[\text{Upper limit} = M + (t_{CL})(s_M)\]
де\(M\) - середнє значення вибірки,\(t_{CL}\) - це бажаний рівень довіри (\(0.95\)у наведеному вище прикладі), і\(s_M\) є розрахунковою стандартною похибкою середнього.\(t\)
Закінчимо з аналізом даних Stroop. Зокрема, ми обчислимо довірчий інтервал на середній бал різниці. Нагадаємо, що\(47\) піддослідні назвали колір чорнила, якими були написані слова. Назви конфліктували так, що, наприклад, вони назвали колір чорнила слова «синій», написаного червоним чорнилом. Правильна відповідь - сказати «червоний» і ігнорувати той факт, що слово «синій». У другій умові суб'єкти назвали чорнильним кольором кольорових прямокутників.
| Іменування кольорового прямокутника | перешкоди | Різниця |
|---|---|---|
| 17 | 38 | 21 |
| 15 | 58 | 43 |
| 18 | 35 | 17 |
| 20 | 39 | 19 |
| 18 | 33 | 15 |
| 20 | 32 | 12 |
| 20 | 45 | 25 |
| 19 | 52 | 33 |
| 17 | 31 | 14 |
| 21 | 29 | 8 |
Таблиця\(\PageIndex{2}\) показує різницю в часі між інтерференцією та умовами іменування кольорів для\(10\)\(47\) суб'єктів. Середня різниця в часі для всіх\(47\) суб'єктів становить\(16.362\) секунди, а стандартне відхилення -\(7.470\) секунди. Стандартна похибка середнього значення є\(1.090\). \(t\)Таблиця показує критичне значення\(t\) для\(47 - 1 = 46\) ступенів свободи є\(2.013\) (для\(95\%\) довірчого інтервалу). Тому довірчий інтервал обчислюється наступним чином:
\[\text{Lower limit} = 16.362 - (2.013)(1.090) = 14.17\]
\[\text{Upper limit} = 16.362 - (2.013)(1.090) = 18.56\]
Тому ефект перешкод (різниця) для всієї популяції, ймовірно, буде між\(14.17\) і\(18.56\) секундами.
