10.8: т Розподіл

Last updated
Save as PDF

Page ID: 98032

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Створіть різницю між формою\(t\) розподілу та нормальним розподілом
Створіть, як на різницю між формою\(t\) розподілу та нормальним розподілом впливають ступені свободи
Використовуйте\(t\) таблицю, щоб знайти значення\(t\) для використання в довірчому інтервалі
Використовуйте\(t\) калькулятор, щоб знайти значення\(t\) для використання в довірчому інтервалі

При введенні до\(95\%\) нормальних розподілів було показано, що площа нормального розподілу знаходиться в межах\(1.96\) стандартних відхилень від середнього. Тому, якщо ви випадковим чином вибрали значення з нормального розподілу із середнім значенням\(100\), ймовірність, що воно буде в межах\(1.96\sigma \)\(100\) є\(0.95\). Аналогічно, якщо ви\(N\) виберете значення з популяції, ймовірність того, що вибірковий середній (\(M\)) буде знаходитися в межах\(1.96\sigma _M\)\(100\) дорівнює\(0.95\).

Тепер розглянемо випадок, в якому у вас нормальний розподіл, але ви не знаєте стандартного відхилення. Ви вибірку\(N\) значень і обчислюєте вибірку середнього (\(M\)) і оцінюєте стандартну похибку середнього (\(\sigma _M\)) с\(s_M\). Яка ймовірність того, що\(M\) буде в межах\(1.96 s_M\) популяції означає (\(\mu\))?

Це складна проблема, оскільки існує два способи, за допомогою яких\(M\) може бути більше, ніж\(1.96 s_M\) від\(\mu\):

\(M\)може, випадково, бути або дуже високим, або дуже низьким і
\(s_M\)може, випадково, бути дуже низьким.

Інтуїтивно має сенс, що ймовірність опинитися в межах\(1.96\) стандартних похибок середнього повинна бути меншою, ніж у випадку, коли стандартне відхилення відомо (і не може бути недооцінено). Але наскільки точно менше? На щастя, спосіб відпрацювання цього типу проблеми був вирішений ще на початку\(20^{th}\) століття У.С. Госсетом, який визначив розподіл середнього, розділеного на оцінку його стандартної похибки. Цей розподіл називається\(t\) розподілом Студента або іноді просто\(t\) розподілом. Госсет розробив\(t\) розподіл та пов'язані з ними статистичні тести під час роботи на пивоварні в Ірландії. Через договірну угоду з пивоварнею він опублікував статтю під псевдонімом «Студент». Саме тому\(t\) тест називається «Студентський\(t\) тест».

\(t\)Розподіл дуже схожий на звичайний розподіл, коли оцінка дисперсії базується на багатьох ступенях свободи, але має відносно більше балів у хвостах, коли менше ступенів свободи. \(\PageIndex{1}\)На малюнку показані\(t\) розподіли з\(2\)\(4\), і\(10\) ступені свободи і стандартний нормальний розподіл. Зверніть увагу, що нормальний розподіл має відносно більше балів у центрі розподілу, а\(t\) розподіл має відносно більше в хвостах. Тому\(t\) розподіл лептокуртіческій. \(t\)Розподіл наближається до нормального розподілу зі збільшенням ступенів свободи.

Малюнок\(\PageIndex{1}\): Порівняння\(t\) розподілів з\(2\)\(4\),\(10\)\(df\) і стандартним нормальним розподілом. Розподіл з найнижчим піком - це\(2\; df\) розподіл, наступний найнижчий -\(4\; df\), найнижчий після цього\(10\; df\), а найвищий - стандартний нормальний розподіл

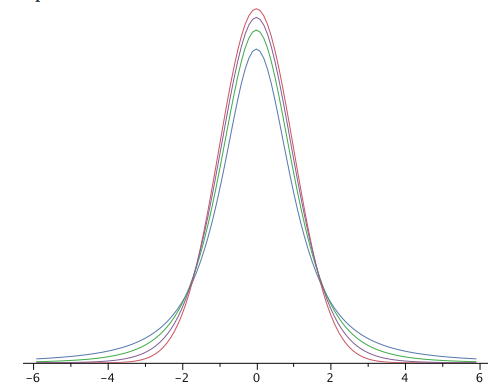
Так як\(t\) розподіл лептокуртіческій, то відсоток розподілу в межах\(1.96\) стандартних відхилень середнього менше, ніж\(95\%\) при нормальному розподілі. Таблиця\(\PageIndex{1}\) показує кількість стандартних відхилень від середнього,\(99\%\) необхідного для утримання,\(95\%\) і площі\(t\) розподілу для різних ступенів свободи. Це значення,\(t\) які ви використовуєте в довірчому інтервалі. Відповідні значення для нормального розподілу є\(1.96\) і\(2.58\) відповідно. Зверніть увагу, що при декількох ступенях свободи значення\(t\) набагато вищі за відповідні значення для нормального розподілу і що різниця зменшується зі збільшенням ступенів свободи. Значення в таблиці\(\PageIndex{1}\) можна отримати з калькулятора «Знайти\(t\) довірчий інтервал».

Таблиця \(\PageIndex{1}\): Скорочена\(t\) таблиця

дф	0,95	0,99
2	4.303	9.925
3	3.182	5.841
4	2.776	4.604
5	2.571	4.032
8	2.306	3.355
10	2.228	3.169
20	2.086	2.845
50	2.009	2.678
100	1,984	2.626

Повертаючись до задачі, поставленої на початку цього розділу, припустимо, ви\(9\) вибрали значення з нормальної сукупності і оцінили стандартну похибку середнього (\(\sigma _M\)) с\(s_M\). Яка ймовірність, що\(M\) буде в межах\(1.96 s_M\)\(\mu\)? Так як розмір вибірки є\(9\), є\(N - 1 = 8 df\). З таблиці\(\PageIndex{1}\) видно, що з великою\(8 df\) ймовірністю є\(0.95\) те, що середнє буде в межах\(2.306 s_M\)\(\mu\). Імовірність того, що вона буде знаходитися в межах\(1.96 s_M\)\(\mu\), тому нижча, ніж\(0.95\).

Як показано на малюнку\(\PageIndex{2}\), калькулятор "\(t\)розподілу» може бути використаний, щоб знайти, що\(0.086\) площа\(t\) розподілу більше, ніж\(1.96\) стандартні відхилення від середнього, тому ймовірність того, що\(M\) буде менше, ніж\(1.96 s_M\) від\(\mu\) є\(1 - 0.086 = 0.914\).

Малюнок\(\PageIndex{2}\): Площа більше\(1.96\) стандартних відхилень від середнього в\(t\) розподілі с\(8 df\). Зверніть увагу, що двоххвоста кнопка вибирається так, що область в обох хвостах буде включена

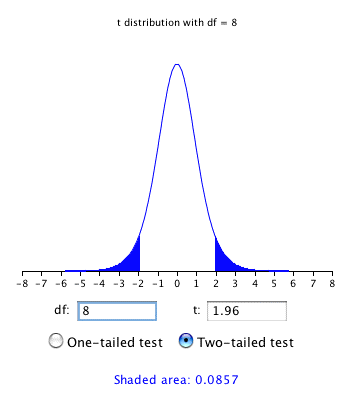
Як і очікувалося, ця ймовірність менша\(0.95\), ніж була б отримана, якби\(\sigma _M\) була відома, а не оцінена.