5.8: Біноміальна демонстрація

Last updated
Save as PDF

Page ID: 98305

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Стати, як\(N\) впливає на форму біноміального розподілу

Інструкції

Ця демонстрація дозволяє вивчити біноміальний розподіл. Тут можна вказати кількість випробувань (\(N\)) і частку успіхів (\(p\)). Зверніть увагу, що частка успіхів іноді посилається з грецьким листом\(p\); тут вона буде згадуватися як\(p\).

Початкові значення для\(N\) і\(p\) є\(10\) і\(0.5\). Таким чином, графік показує ймовірність від\(0\) до\(10\) успіхів з\(10\) випробувань. Імовірність\(0\) успіхів настільки мала, що вона ледве з'являється на графіку. Найбільш вірогідна кількість успіхів\(5\), яка має ймовірність приблизно\(0.25\). Природно, сума ймовірностей є\(1.0\).

Демонстрація також показує середнє і стандартне відхилення біноміального розподілу.

Ілюстровані інструкції

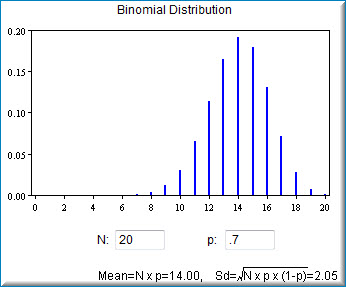
На знімку екрана нижче показано біноміальну демонстрацію з даними за замовчуванням. Ви можете налаштувати кількість випробувань (\(N\)), а також частку успіхів (\(p\)).

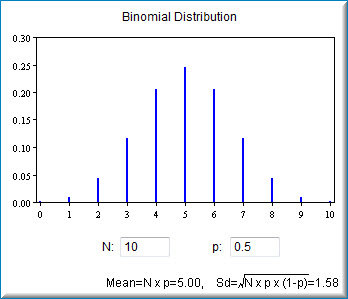
біноміальний 5.8.1.jpg — Малюнок\(\PageIndex{1}\): Біноміальна демонстрація з даними за замовчуванням

У наведеному нижче прикладі показано розподіл\(20\) випробувань з ймовірністю успіху\(0.7\). Зверніть увагу, що також показано середнє та стандартне відхилення для розподілу.

біноміальний 5.8.2.jpg — Малюнок\(\PageIndex{1}\): Біноміальний розподіл 20 випробувань