Skip to main content
LibreTexts - Ukrayinska

3.14: Оцінка моделювання дисперсії

  1. Last updated
  2. Save as PDF
  • Page ID
    98148

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    • Дізнайтеся, яка міра центральної тенденції збалансує розподіл

    Інструкції

    Це моделювання вибірки з популяції\(50\) чисел, показані тут. Ви можете бачити, що існують\(10\) екземпляри значень\(1, 2, 3, 4\), і\(5\). Отже, середнє значення населення є\(3\). Дисперсія являє собою середнє квадратне відхилення від середнього значення\(3\). Ви можете обчислити, що це саме так\(2\).

    При натисканні на кнопку «Намалювати\(4\) номери» проводиться вибірка чотирьох балів (з заміною) з населення. Чотири числа показані червоним кольором, як і середнє значення чотирьох чисел. Потім дисперсія обчислюється двома способами. Верхня формула обчислює дисперсію шляхом обчислення середнього квадрату відхилень або чотирьох вибіркових чисел із середнього зразка. Нижня формула обчислює середнє значення квадратних відхилень або чотири вибіркових чисел від середнього значення популяції\(3.00\) (у рідкісних випадках вибірка та засоби популяції будуть рівними). Обчислені відхилення розміщуються в полах праворуч від формул. Середнє значення значень у полі показано внизу поля. Коли в полі є тільки одне значення, середнє значення, звичайно, дорівнюватиме цьому значенню.

    Якщо ви знову натиснете кнопку «Намалювати\(4\) номери», будуть вибрані ще чотири числа. Середнє значення і дисперсія також будуть обчислюватися, як і раніше. Поля праворуч від формул міститимуть обидві дисперсії, а внизу поля буде показано середнє значення відхилень.

    Дисперсія населення точно\(2\). Використовуйте цей факт для оцінки відносного значення двох формул для дисперсії. Подивіться, який з них, в середньому, підходить,\(2\) а який дає нижчі оцінки. Вивчіть, чи завжди формула є більш точною, або іноді одна є більш точною, а в інший час інша формула є. Якщо дисперсія на основі середнього зразка була обчислена шляхом ділення на\(N-1 = 3\) замість\(4\), то дисперсія була б у\(\tfrac{4}{3}\) рази більшою. Чи\(\tfrac{4}{3}\) призводить множення дисперсії до кращих оцінок?

    Ілюстровані інструкції

    Як видно на скріншоті нижче, моделювання оцінки дисперсії починається з відображення кількості\(50\) чисел, починаючи від\(1 - 5\).

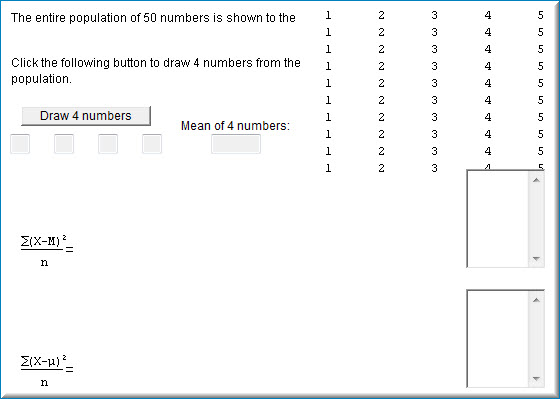
    variance_est1.jpg
    Малюнок\(\PageIndex{1}\): Моделювання оцінки V дисперсії

    При кожному натисканні кнопки «Намалювати\(4\) числа» чотири числа вибірки з населення і середнє, дисперсія вибірки від середнього зразка, а також дисперсія вибірки від середнього значення популяції. Розбіжності зберігаються в полах поруч із відповідною формулою. На скріншоті нижче показано моделювання після того, як кнопка «Намалювати\(4\) цифри» була натиснута чотири рази.

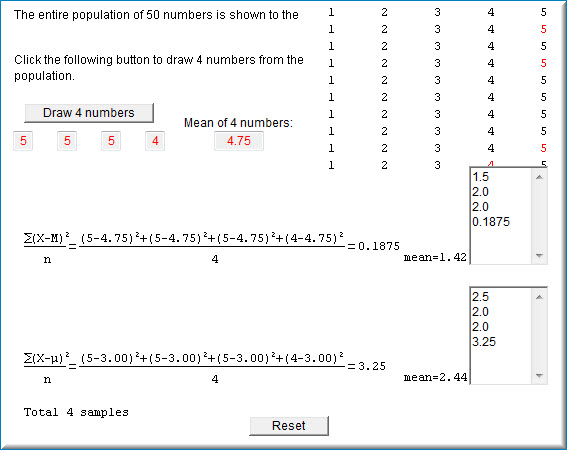
    variance_est2.jpg
    Малюнок\(\PageIndex{2}\): Моделювання після натискання кнопки «Намалювати\(4\) номери»

    Використовуйте моделювання, щоб вивчити, чи є будь-яка формула в середньому більш точною, ніж інша.