3.15: Форми дистрибутивів

Last updated
Save as PDF

Page ID: 98171

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Обчислення перекосу за допомогою двох різних формул
Обчислення куртозу

Ми побачили в розділі про розподіли в Главі 1, що форми розподілів можуть відрізнятися перекосом та/або куртозом. У цьому розділі представлені числові показники цих двох мір форми.

Перекіс

$\PageIndex{1}$На малюнку показано розподіл з дуже великим позитивним перекосом. Нагадаємо, що розподіли з позитивним перекосом мають хвости, які тягнуться вправо.

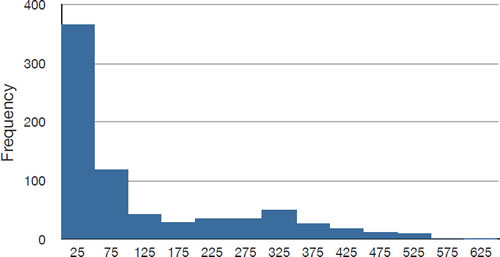
MLB зарплати histo.jpg — Малюнок$\PageIndex{1}$: Розподіл з дуже великим позитивним перекосом. Ця гістограма показує зарплати гравців вищої ліги бейсболу (в десятках тисяч доларів).

Розподіли з позитивним перекосом зазвичай мають більші засоби, ніж медіани. Середнє і медіана бейсбольних зарплат, показаних на малюнку$\PageIndex{1}$, є$\$1,183,417$ і$\$500,000$ відповідно. Таким чином, для цього високо перекошеного розподілу середнє значення більш ніж в два рази вище медіани. Зв'язок між перекосом і відносним розміром середнього і медіани змусило статистика Пірсона запропонувати наступний простий і зручний числовий індекс перекосу:

\[\frac{3(Mean-Median)}{\sigma }\]

Стандартне відхилення бейсбольних зарплат є$1,390,922$. Тому міра перекісу Пірсона для цього розподілу є$\dfrac {3(1,183,417 - 500,000)}{1,390,922} = 1.47$.

Подібно до того, як існує кілька заходів центральної тенденції, існує більше однієї міри перекосу. Хоча міра Пірсона є гарною, частіше використовується наступна міра. Його іноді називають третім моментом про середнє.

\[\sum \dfrac {(X-\mu )^3}{\sigma ^3}\]

Куртоз

Наступна міра куртоза аналогічна визначенню перекосу. Значення "$3$" віднімається для визначення «no kurtosis» як куртозу нормального розподілу. В іншому випадку нормальний розподіл мав би куртоз$3$.

\[\sum \dfrac {(X-\mu )^4}{\sigma ^4}-3\]