3.6: Моделювання квадратних відмінностей
- Page ID
- 98158
Цілі навчання
- Дізнайтеся, яка міра центральної тенденції мінімізує суму квадратних відхилень
Інструкції
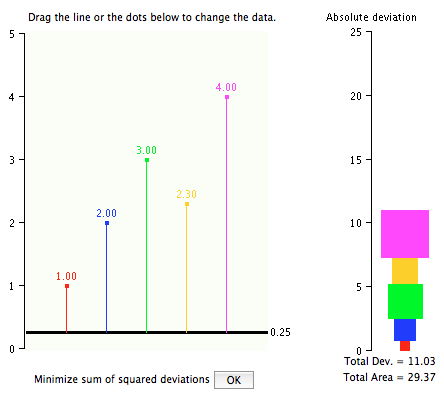
Ця демонстрація дозволяє досліджувати суму квадратів відхилень від заданого значення. На графіку праворуч показані числа\(1, 2, 3, 4,\)\(5\) і їх відхилення від довільного початкового значення\(0.254\) (цифра відображає це округлено до\(0.25\)).
Перше число,\(1\), представлено червоною крапкою. Відхилення від\(0.254\) представлено червоною лінією від червоної точки до чорної лінії. Значення чорної лінії дорівнює\(0.254\).
Аналогічно число\(2\) представлено синьою крапкою і його відхилення від\(0.25\) представлено синьою лінією.
Висота кольорових прямокутників являє собою суму абсолютних відхилень від чорної лінії. Сума відхилень чисел\(1, 2, 3, 4,\) і\(5\) від\(0.25\) є\(0.746 + 1.75 + 2.746 + 3.746 + 4.746 = 13.73\).
Площа кожного прямокутника представляє величину квадратного відхилення точки від чорної лінії. Наприклад, червоний прямокутник має площу\(0.746\times 0.746 = 0.557\). Сума всіх площ прямокутників дорівнює\(47.70\). Сума всіх площ являє собою суму квадратів відхилень.
У цій демонстрації ви можете перемістити чорну смугу, натиснувши на неї і перетягнувши її вгору або вниз. На другому малюнку він був переміщений вгору\(1.0\). Відхилення червоної точки від чорної смуги тепер,\(0\) оскільки вони обидва\(1\). Сума відхилень тепер\(10 (0 + 1 + 2 + 3 + 4)\) і сума квадратних відхилень дорівнює\(30 (0^2 + 1^2 + 2^2 + 3^2 + 4^2)\).
У міру переміщення смуги вгору і вниз змінюється значення суми абсолютних відхилень і суми квадратних відхилень.
Подивіться, чи зможете ви знайти розташування чорної смуги, яка дає найменше значення для суми квадратів відхилень.
Щоб перевірити і подивитися, чи знайшли ви найменше значення, натисніть кнопку «ОК» внизу графіка. Він перемістить планку в місце, яке виробляє найменшу суму квадратних відхилень.
Для вихідних даних величина, яка мінімізує суму квадратних відхилень, також є величиною, яка мінімізує суму абсолютних відхилень. Це не буде вірно для більшості даних.
Ви також можете переміщати окремі точки. Натисніть на одну з точок і перемістіть її вгору або вниз і зверніть увагу на ефект. Ваша мета для цієї демонстрації полягає в тому, щоб виявити правило для визначення того, яке значення дасть вам найменшу суму квадратних відхилень.
Ілюстровані інструкції
Нижче наведено знімок екрана початкового екрана моделювання. «Загальна дев.» - це сума абсолютних відхилень; «Загальна площа» - сума квадратних відхилень.
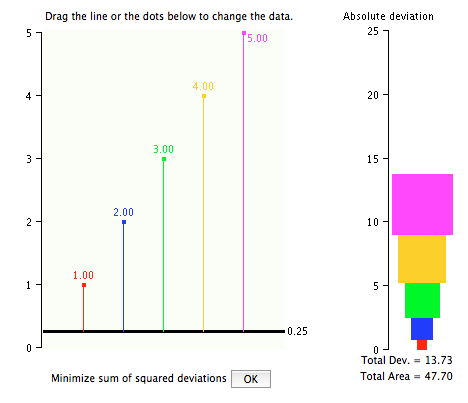
Нижче наведено приклад після зміни вертикальної лінії. Відстані до лінії були перераховані.
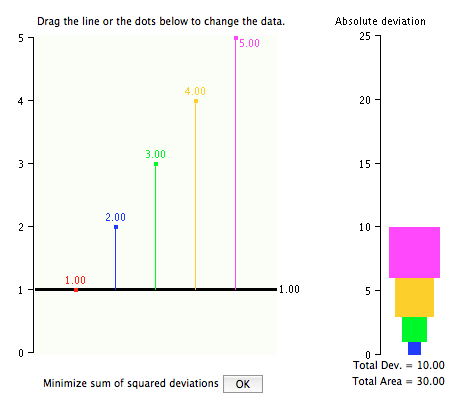
Ви можете змінити дані, натиснувши на точку даних і перетягуючи. Приклад зі зміненими даними наведено нижче.