3.7: Середнє і середнє

Last updated
Save as PDF

Page ID: 98170

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Стан, будь то середнє або медіана, що мінімізує середнє абсолютне відхилення
Вкажіть, чи це середнє або медіана, що є точкою балансу за шкалою балансу

У розділі «Що таке центральна тенденція» ми побачили, що центр розподілу можна визначити трьома способами:

точка, на якій розподіл буде балансувати
значення, середнє абсолютне відхилення якого від усіх інших значень зведено до мінімуму
значення, середня різниця якого в квадраті від всіх інших значень зведена до мінімуму

З моделювання в цьому розділі ви виявили (ми сподіваємося), що середнє значення - це точка, на якій розподіл буде балансувати, медіана - це значення, яке мінімізує суму абсолютних відхилень, а середнє значення - це значення, яке мінімізує суму квадратних відхилень.

Таблиця\(\PageIndex{1}\) показує абсолютні і квадратні відхилення чисел\(2, 3, 4, 9\) і\(16\) від їх медіани\(4\) і їх середнього значення\(6.8\). Можна помітити, що сума абсолютних відхилень від медіани (\(20\)) менше суми абсолютних відхилень від середнього (\(22.8\)). З іншого боку, сума квадратних відхилень від медіани (\(174\)) більше суми квадратних відхилень від середнього (\(134.8\)).

Таблиця\(\PageIndex{1}\): Абсолютні і квадратні відхилення від медіани 4 і середнє значення 6,8
Значення	Абсолютне відхилення від медіани	Абсолютне відхилення від середнього	Квадратне відхилення від медіани	Відхилення у квадраті від середнього
2	2	4.8	4	23.04
3	1	3.8	1	14.44
4	0	2.8	0	7.84
9	5	2.2	25	4.84
16	12	9.2	144	84.64
Всього	20	22.8	174	134,8

\(\PageIndex{1}\)На малюнку показано, що розподіл залишків на середньому\(6.8\) рівні, а не на медіані\(4\). Відносні переваги та недоліки середнього та медіани розглядаються в розділі «Порівняння заходів» далі в цьому розділі.

Малюнок\(\PageIndex{1}\): Баланси розподілу на середнє значення,\(6.8\) а не на медіані\(4.0\).

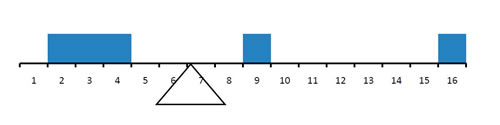
Коли розподіл симетричний, то середнє і медіана однакові. Розглянемо наступний розподіл:\(1, 3, 4, 5, 6, 7, 9\). Середнє і медіана обидва\(5\). Середнє, медіана і режим ідентичні в дзвоноподібному нормальному розподілі.