2.6: Коробкові ділянки
- Page ID
- 98146
Цілі навчання
- Визначте основні терміни, включаючи петлі, H-спред, крок, суміжне значення, зовнішнє значення та віддалене значення
- Створюємо ділянку коробки
- Створення паралельних графіків коробки
- Визначте, чи підходить графік коробки для заданого набору даних
Ми вже обговорювали методи візуального представлення даних (див. Гістограми та частотні полігони). У цьому розділі ми представляємо ще один важливий графік, який називається графіком коробки. Графіки коробки корисні для ідентифікації викидів та порівняння розподілів. Ми пояснимо графіки коробки за допомогою даних з експерименту в класі. В рамках «Stroop interference Case Study» студентам у вступній статистиці була представлена сторінка, що містить\(30\) кольорові прямокутники. Їх завдання полягало в тому, щоб якомога швидше назвати кольори. Їх часи (в секундах) були зафіксовані. Ми порівняємо результати для\(16\) чоловіків і\(31\) жінок, які брали участь в експерименті, склавши окремі сюжети коробки для кожної статі. Такий дисплей, як кажуть, передбачає паралельні ділянки коробки.
Існує кілька етапів побудови коробчатого ділянки. Перший спирається на\(25^{th},\; 50^{th},\; and\; 75^{th}\) процентилі при розподілі балів. \(\PageIndex{1}\)На малюнку показано, як використовуються ці три статистичні дані. Для кожного статі малюємо коробку, що проходить від\(25^{th}\) процентиля до\(75^{th}\) процентиля. \(50^{th}\)Процентиль малюється всередині коробки. Тому,
- дно кожного ящика -\(25^{th}\) процентиль,
- вершина -\(75^{th}\) процентиль,
- а лінія посередині -\(50^{th}\) процентиль.
Дані для жінок в нашій вибірці наведені в табл\(\PageIndex{1}\).
| 14 | 17 | 18 | 19 | 20 | 21 | 29 |
| 15 | 17 | 18 | 19 | 20 | 22 | |
| 16 | 17 | 18 | 19 | 20 | 23 | |
| 16 | 17 | 18 | 20 | 20 | 24 | |
| 17 | 18 | 18 | 20 | 21 | 24 |
Для цих даних\(25^{th}\) процентиль - це\(17\),\(50^{th}\) процентиль -\(19\), а\(75^{th}\) процентиль -\(20\). Для чоловіків (чиї дані не показані)\(25^{th}\) процентиль - це\(19\),\(50^{th}\) процентиль -\(22.5\), а\(75^{th}\) процентиль -\(25.5\).
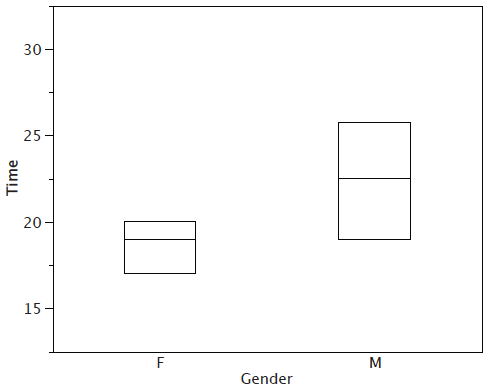
Перш ніж продовжити, корисна термінологія в таблиці\(\PageIndex{2}\).
| Ім'я | Формула | Значення |
|---|---|---|
| Верхній шарнір | 75-й процентиль | 20 |
| Нижня петля | 25-й процентиль | 17 |
| H-спред | Верхня петля - Нижня петля | 3 |
| Крок | 1,5 х H-спред | 4.5 |
| Верхній внутрішній паркан | Верхній шарнір+1 крок | 24.5 |
| Нижня внутрішня огорожа | Нижня петля - 1 крок | 12.5 |
| Верхній зовнішній паркан | Верхній шарнір+2 кроки | 29 |
| Нижня зовнішня огорожа | Нижня петля - 2 сходинки | 8 |
| Верхній суміжний | Найбільше значення нижче верхнього внутрішнього паркану | 24 |
|
Нижній суміжний |
Найменше значення вище нижнього внутрішнього паркану | 14 |
| Зовнішнє значення | Значення поза внутрішнім парканом, але не за межами зовнішньої огорожі | 29 |
| Далеке значення | Значення за межами зовнішньої огорожі | Жоден |
Продовжуючи з ділянками коробки, ми ставимо «вуса» вище і під кожною коробкою, щоб дати додаткову інформацію про поширення даних. Вуса - це вертикальні лінії, які закінчуються горизонтальним штрихом. Вуса малюються від верхньої і нижньої петель до верхніх і нижніх суміжних значень (\(24\)і\(14\) для жіночих даних).
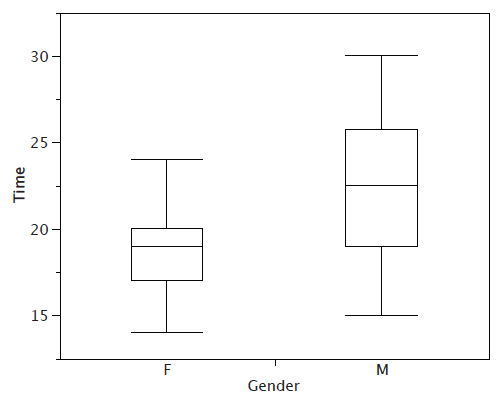
Хоча ми не малюємо вуса аж до зовнішніх або далеких значень, ми все одно хочемо представити їх у наших ділянках коробки. Це досягається додаванням додаткових міток за межі вусів. Зокрема, зовнішні значення позначаються малими\(o's\) "", а далекі значення позначаються зірочками (\(\ast\)). У наших даних немає далеких значень і лише одне зовнішнє значення. Це зовнішнє значення\(29\) є для жінок і показано на малюнку\(\PageIndex{3}\).
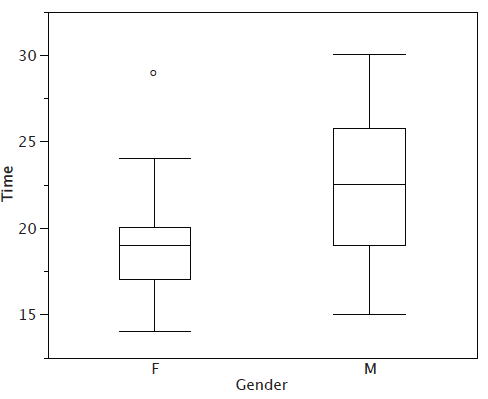
Існує ще одна позначка, яку слід включити в графіки коробки (хоча іноді вона опущена). Вказуємо середній бал для групи, вставивши знак плюс. \(\PageIndex{4}\)На малюнку показаний результат додавання засобів до наших графіків коробки.
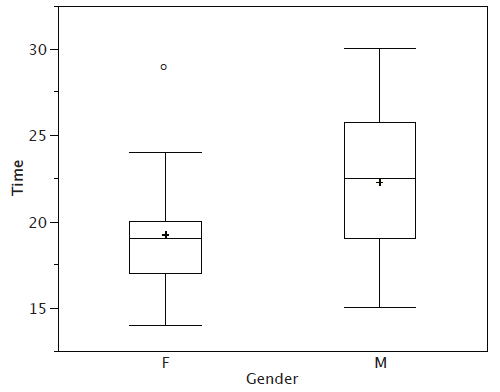
На малюнку\(\PageIndex{4}\) наведено показове резюме даних. Оскільки половина балів у розподілі знаходиться між петлями (нагадаємо, що петлі - це\(25^{th}\) і\(75^{th}\) процентилі), ми бачимо, що половина жіночих часів між\(17\) і\(20\) секундами, тоді як половина чоловічих часів - між\(19\) і\(25.5\). Ми також бачимо, що жінки, як правило, називали кольори швидше, ніж чоловіки, хоча одна жінка була повільнішою, ніж майже всі чоловіки. \(\PageIndex{5}\)На малюнку зображений графік коробки для жіночих даних з докладними мітками.
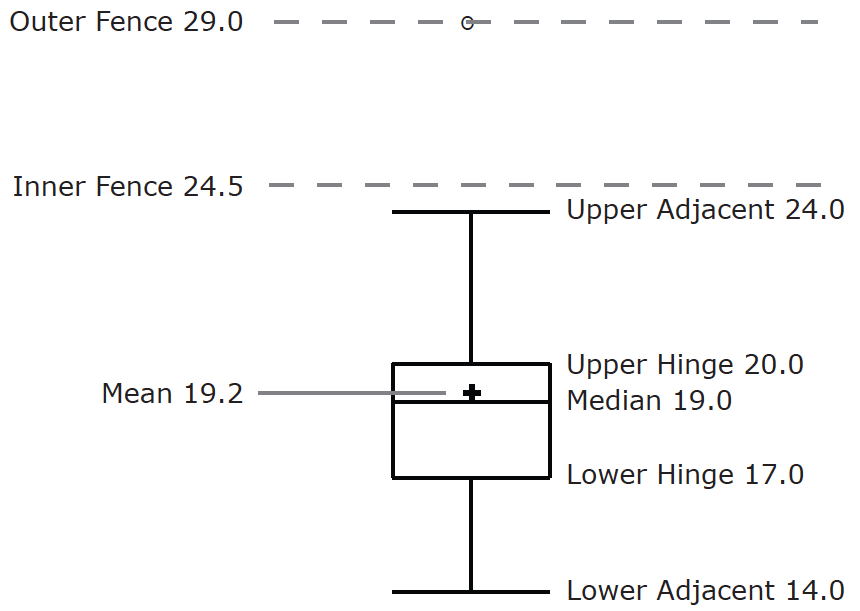
Коробкові ділянки надають основну інформацію про розподіл. Наприклад, розподіл з позитивним перекосом матиме довший вус у позитивному напрямку, ніж у негативному напрямку. Більша середня, ніж медіана, також вказуватиме на позитивний перекіс. Коробкові сюжети добре зображують екстремальні значення і особливо добре демонструють відмінності між розподілами. Однак багато деталей розподілу не розкриваються на графіку коробки, і для вивчення цих деталей слід створити гістограму та/або відображення стебла та листя.
Ось деякі інші приклади графіків коробки:
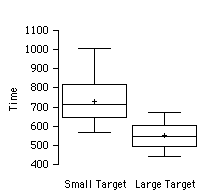
Приклад\(\PageIndex{1}\): Time to move the mouse over a target
Дані надходять із завдання, в якому мета полягає в тому, щоб якомога швидше перемістити комп'ютерну мишу до мети на екрані. На\(20\) одному з випробувань мішенню був невеликий прямокутник\(20\), на іншому мішенню був великий прямокутник. Час досягнення мети фіксувався на кожному випробуванні. Графіки коробки двох розподілів наведені нижче. Ви можете бачити, що хоча в рази є певне перекриття, як правило, потрібно більше часу, щоб перемістити мишу до маленької мети, ніж до великої.
Приклад\(\PageIndex{2}\): Draft lottery
У\(1969\) війні у В'єтнамі була в самому розпалі. Агентству під назвою «Вибіркова служба» було доручено знайти справедливу процедуру визначення того, які молоді люди будуть призвані («покликані») у військові США. Процедура повинна була бути справедливою в сенсі не сприяти будь-якій культурно чи економічно визначеній підгрупі американських чоловіків. Було вирішено, що вибір «призовників» виключно виходячи з дати народження людини буде справедливим. Таким чином, була розроблена лотерея на день народження. Шматочки паперу, що представляють\(366\) дні року (в тому числі\(\text{February 29}\)), поміщали в пластикові капсули, заливали в обертовий барабан, а потім вибирали по одному. Чим менший номер проекту, тим швидше людина буде складена. Чоловіки з досить високими числами взагалі не були розібрані.
Перше число було вибрано\(258\), що означало, що хтось, хто народився в\(258^{th}\) день року (\(\text{September 14}\)), буде одним з перших, хто буде складений. Друге число було\(115\), тому хтось, хто народився на 1\(15^{th}\) день (\(\text{April 24}\)) був серед другої групи, яку потрібно скласти. Всім датам\(366\) народження привласнювалися чернеткові номери таким чином.
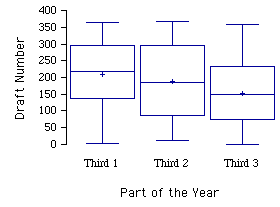
Для обрешітки коробчатих ділянок ми розділили\(366\) дні року на третини. Перша третина йде від\(\text{January 1 to May 1}\), друга з\(\text{May 2 to August 31}\), а остання з\(\text{September 1 to December 31}\). Три групи дат народження дають три групи чернеткових чисел. Чернетковий номер на кожен день народження - це порядок, який він був підібраний на розіграші. На малюнку нижче наведено графіки коробки з трьох наборів чорнових номерів. Як бачите, люди, народжені пізніше року, мали менші числа чернетки.
Варіації на коробкових ділянках
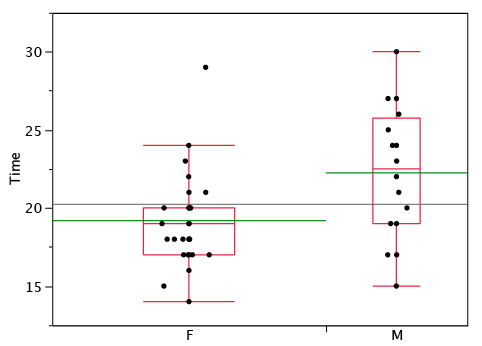
Програми статистичного аналізу можуть пропонувати варіанти того, як створюються графіки коробки. Наприклад, графіки коробки на малюнку\(\PageIndex{8}\) побудовані з наших даних, але відрізняються від попередніх ділянок коробки кількома способами.
- Він не позначає викидів.
- Засоби позначаються зеленими лініями, а не знаками «плюс».
- Середнє значення всіх балів позначається сірою лінією.
- Окремі бали представлені крапками. Оскільки бали були округлені до найближчої секунди, будь-яка задана точка може представляти більше одного балу.
- Коробка для жінок ширша, ніж коробка для чоловіків, оскільки ширина ящиків пропорційна кількості предметів кожної статі (\(31\)жінок і\(16\) чоловіків).
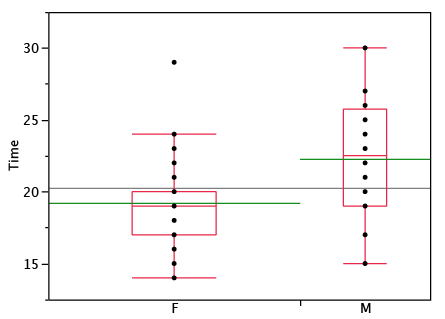
Кожна точка на малюнку\(\PageIndex{8}\) представляє групу предметів з однаковою оцінкою (округлена до найближчої секунди). Альтернативною технікою графіки є тремтіння точок. Це означає поширення різних точок в одному горизонтальному положенні, по одній точці для кожного предмета. Точне горизонтальне положення точки визначається випадковим чином (за умови, що різні точки не перекриваються точно). Розкидання крапок допоможе вам побачити кілька випадків заданої оцінки. Однак, залежно від розміру точки та роздільної здатності екрана, деякі точки можуть бути затемнені, навіть якщо точки тремтяться. \(\PageIndex{9}\)На малюнку показано, як виглядає тремтіння.
Різні стилі сюжетів коробки найкраще підходять для різних ситуацій, і немає твердих правил, для яких можна використовувати. Вивчаючи свої дані, ви повинні спробувати кілька способів їх візуалізації. Які графіки ви включаєте у свій звіт, повинні залежати від того, наскільки добре різні графіки розкривають аспекти даних, які ви вважаєте найбільш важливими.
