Skip to main content
LibreTexts - Ukrayinska

2.5: Багатокутники частоти

  1. Last updated
  2. Save as PDF
  • Page ID
    98126

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    • Створення та інтерпретація частотних багатокутників
    • Створення та інтерпретація кумулятивних частотних багатокутників
    • Створення та інтерпретація накладених частотних багатокутників

    Частотні багатокутники - це графічний пристрій для розуміння форм розподілів. Вони служать тій же меті, що і гістограми, але особливо корисні для порівняння наборів даних. Частотні полігони також є хорошим вибором для відображення кумулятивних розподілів частоти.

    Щоб створити частотний багатокутник, почніть так само, як і для гістограм, вибравши інтервал класу. Потім намалюйте\(X\)-axis representing the values of the scores in your data. Mark the middle of each class interval with a tick mark, and label it with the middle value represented by the class. Draw the \(Y\)-axis to indicate the frequency of each class. Place a point in the middle of each class interval at the height corresponding to its frequency. Finally, connect the points. You should include one class interval below the lowest value in your data and one above the highest value. The graph will then touch the \(X\)-axis on both sides.

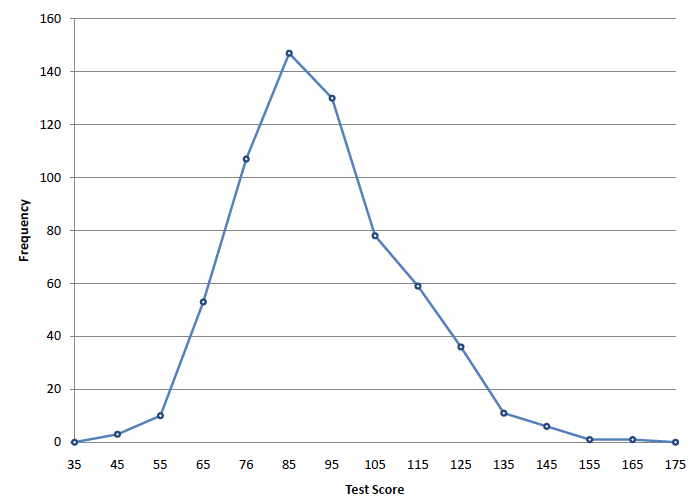
    freq_poly.jpg
    Малюнок\(\PageIndex{1}\): Частотний багатокутник для результатів тестування психології

    Частотний багатокутник для тестових балів\(642\) психології, показаних на малюнку,\(\PageIndex{1}\) був побудований з таблиці частот, наведеної в табл\(\PageIndex{1}\).

    Таблиця\(\PageIndex{1}\): Частотний розподіл балів тестів психології.
    Нижня межа Верхня межа Граф Накопичувальний підрахунок
    29.5 39.5 0 0
    39.5 49.5 3 3
    49.5 59,5 10 13
    59,5 69.5 53 66
    69.5 79.5 107 173
    79.5 89.5 147 320
    89.5 99.5 130 450
    99.5 109.5 78 528
    109.5 119,5 59 587
    119,5 129.5 36 623
    129.5 139.5 11 634
    139.5 149.5 6 640
    149.5 159.5 1 641
    159.5 169.5 1 642
    169.5 179.5 0 642

    Перша мітка на\(X\) -осі є\(35\). Це являє собою інтервал, що триває від\(29.5\) до\(39.5\). Оскільки найнижча оцінка тесту\(46\), цей інтервал має частоту\(0\). Позначена точка\(45\) представляє інтервал від\(39.5\) до\(49.5\). У цьому інтервалі три бали. Є\(147\) бали в інтервалі, який оточує\(85\).

    Ви можете легко розрізнити форму розподілу по малюнку\(\PageIndex{1}\). Більшість балів знаходяться між\(65\) і\(115\). Зрозуміло, що розподіл не симетричний, оскільки хороші бали (праворуч) відстежуються більш поступово, ніж погані бали (зліва). У термінології глави 3 (де ми будемо вивчати форми розподілів більш систематично) розподіл перекошений.

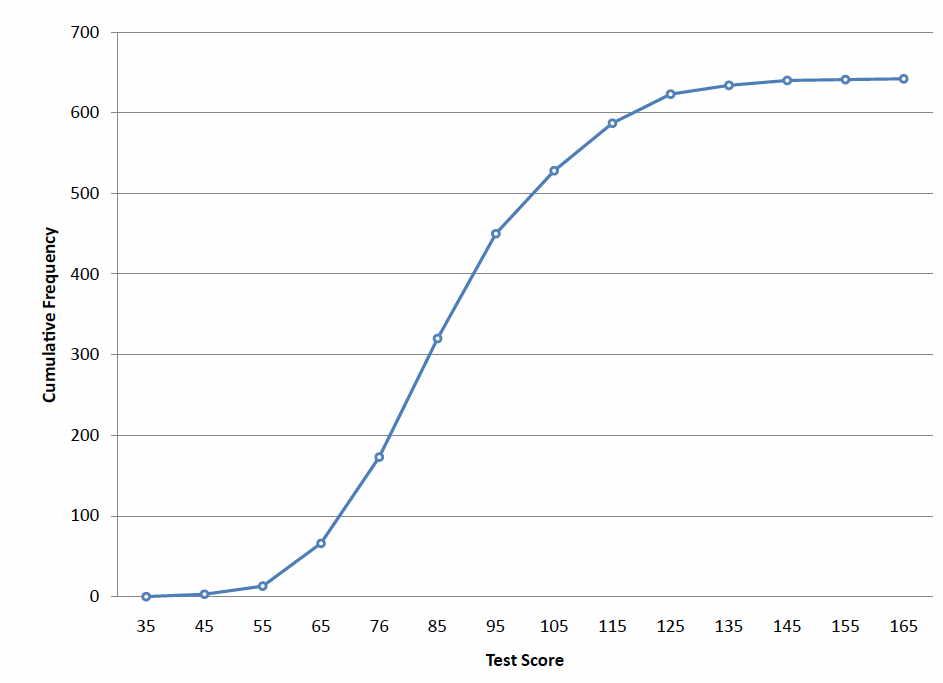
    cumulative.jpg
    Малюнок\(\PageIndex{2}\): Сукупний частотний багатокутник для тестових балів психології

    Сукупний частотний багатокутник для тих же тестових балів показаний на малюнку\(\PageIndex{2}\). Графік такий же, як і раніше, за винятком того, що\(Y\) значення для кожної точки - це кількість учнів у відповідному класі інтервалу плюс всі числа в нижчих інтервалах. Наприклад, немає балів в проміжку з позначкою\(35\), три в інтервалі\(45\), а\(10\) в інтервалі\(55\). Тому\(Y\) значення, відповідне "\(55\)", є\(13\). Оскільки\(642\) студенти здали тест, то сукупна частота для останнього інтервалу становить\(642\).

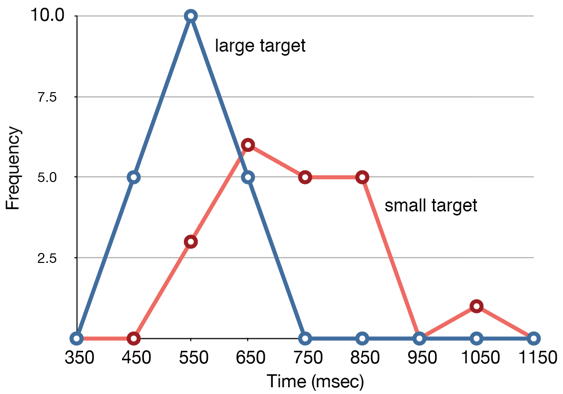
    overlay_freq.jpg
    Малюнок\(\PageIndex{3}\): Накладені частотні багатокутники

    Частотні полігони корисні для порівняння розподілів. Це досягається шляхом накладання частотних полігонів, намальованих для різних наборів даних. На малюнку\(\PageIndex{3}\) наведено приклад. Дані надходять із завдання, в якому мета полягає в тому, щоб якомога швидше перемістити курсор комп'ютера до мети на екрані. На\(20\) одному з випробувань мішенню був невеликий прямокутник\(20\), на іншому мішенню був великий прямокутник. Час досягнення мети фіксувався на кожному випробуванні. Два розподіли (по одному для кожної цілі) побудовані разом на малюнку\(\PageIndex{3}\). На малюнку видно, що, хоча в рази є деяке перекриття, як правило, потрібно більше часу, щоб перемістити курсор до маленької мети, ніж до великої.

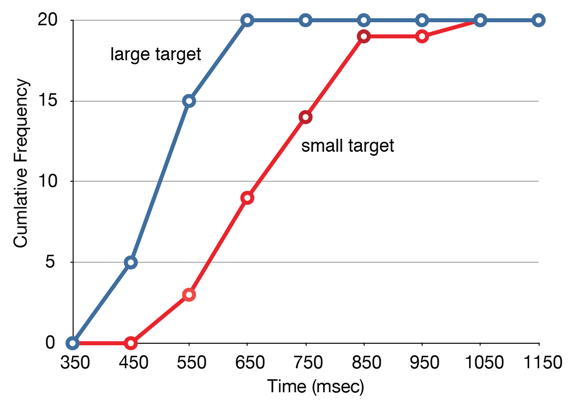
    overlaid_cum_frequency.jpg
    Малюнок\(\PageIndex{1}\): Накладені багатокутники кумулятивної частоти

    Також можлива побудова двох кумулятивних розподілів частот на одному графіку. Це показано на малюнку,\(\PageIndex{4}\) використовуючи ті самі дані з завдання курсора. Різниця в розподілах для двох цілей знову очевидна.