2.4: Гістограми

Last updated
Save as PDF

Page ID: 98134

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Створення згрупованого розподілу частот
Створення гістограми на основі згрупованого розподілу частот
Визначте відповідну ширину бункера

Гістограма - це графічний метод відображення форми розподілу. Це особливо корисно, коли є велика кількість спостережень. Почнемо з прикладу, що складається з балів\(642\) студентів на тесті з психології. Тест складається з\(197\) пунктів, кожен з яких оцінюється як «правильний» або «неправильний». Оцінки студентів варіювалися від\(46\) до\(167\).

Насамперед необхідно створити частотну таблицю. На жаль, проста таблиця частот була б занадто великою, що містить більше\(100\) рядків. Щоб спростити таблицю, групуємо бали разом, як показано в табл\(\PageIndex{1}\).

Таблиця\(\PageIndex{1}\): *Згрупований розподіл частоти психології тестових балів*
Нижня межа інтервалу	Верхня межа інтервалу	Клас частоти
39.5	49.5	3
49.5	59,5	10
59,5	69.5	53
69.5	79.5	107
79.5	89.5	147
89.5	99.5	130
99.5	109.5	78
109.5	119,5	59
119,5	129.5	36
129.5	139.5	11
139.5	149.5	6
149.5	159.5	1
159.5	169.5	1

Для створення цієї таблиці діапазон балів був розбитий на інтервали, звані класовими інтервалами. Перший інтервал - від\(39.5\) до\(49.5\), другий від\(49.5\) до і\(59.5\) т.д. далі для отримання частот класу підраховувалося кількість балів, що потрапляють в кожен інтервал. Є три бали в першому інтервалі,\(10\) у другому і т.д.

Класові інтервали ширини\(10\) забезпечують достатню деталізацію розподілу, щоб виявити, не роблячи графік занадто «нерівним». Більш детальна інформація про вибір ширини інтервалів класів представлена далі в цьому розділі. Розміщення меж інтервалів класів між двома числами (наприклад,\(49.5\)) гарантує, що кожен бал буде падати в інтервалі, а не на межі між інтервалами.

У гістограмі частоти класу представлені смугами. Висота кожної планки відповідає його класу частоти. Гістограма цих даних показана на малюнку\(\PageIndex{1}\).

Малюнок\(\PageIndex{1}\): Гістограма балів на тесті з психології.

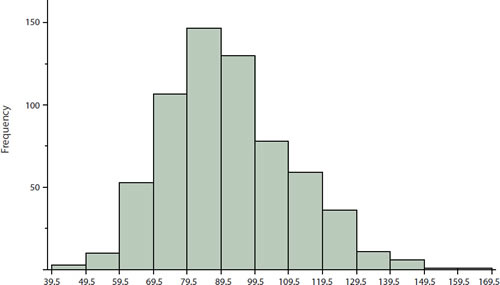
Гістограма дає зрозуміти, що більшість балів знаходяться в середині розподілу, з меншою кількістю балів в крайності. Ви також можете бачити, що розподіл не симетричний: бали поширюються вправо далі, ніж ліворуч. Тому розподіл, як кажуть, перекошений. (Ми будемо більше сказати про форми дистрибутивів у розділі "Підсумовуючи розподіли».)

У нашому прикладі спостереження є цілими числами. Гістограми також можна використовувати, коли бали вимірюються за більш безперервною шкалою, наприклад, тривалості часу (у мілісекундах), необхідного для виконання завдання. У цьому випадку не потрібно турбуватися про паркан-сіттерів, оскільки вони неймовірні. (Було б цілком випадково, щоб завдання вимагало рівно\(7\) секунд, виміряних до найближчої тисячної частки секунди.) Тому ми можемо вибирати цілі числа як межі для інтервалів нашого класу, наприклад\(4000,\; 5000\), тощо Частота класу - це кількість спостережень, які більше або рівні нижньої межі, і строго менше верхньої межі. Наприклад, один інтервал може утримувати час від\(4000\) до\(4999\) мілісекунд. Використання цілих чисел в якості кордонів дозволяє уникнути захаращеного вигляду, і це практика багатьох комп'ютерних програм, які створюють гістограми. Зверніть увагу також, що деякі комп'ютерні програми позначають середину кожного інтервалу, а не кінцеві точки.

Гістограми можуть базуватися на відносних частотах замість фактичних частот. Гістограми, засновані на відносних частотах, показують частку балів у кожному інтервалі, а не кількість балів. У цьому випадку\(Y\) -вісь проходить від\(0\) до\(1\) (або десь між ними, якщо немає крайніх пропорцій). Ви можете змінити гістограму на основі частот на одну, засновану на відносних частотах, (а) розділивши частоту кожного класу на загальну кількість спостережень, а потім (b) побудувавши коефіцієнти на осі\(Y\) -осі (позначені як пропорція).

Правило Стерджеса

Більше можна сказати про ширини інтервалів класів, іноді званих шириною бункера. Вибір ширини бункера визначає кількість інтервалів класів. Це рішення поряд з вибором відправної точки для першого інтервалу впливає на форму гістограми. Є деякі «емпіричні правила», які можуть допомогти вам вибрати відповідну ширину. (Але майте на увазі, що жодне з правил не є ідеальним.) Правило Стерджеса полягає в тому, щоб встановити кількість інтервалів якомога ближче до того\(1 + \log_2(N)\), де\(\log_2(N)\) знаходиться базовий\(2\) журнал кількості спостережень. Формулу також можна записати як\(1 + 3.3\log_2(N)\), де\(\log_{10}(N)\) знаходиться база\(10\) журналу кількості спостережень. Згідно з правилом Стерджеса,\(1000\) спостереження будуть позначені з інтервалами\(11\) класів, оскільки\(10\) є найближчим цілим числом до\(\log_2(1000)\). Ми віддаємо перевагу правилу Рису, яке полягає у встановленні кількості інтервалів у два рази більше кубового кореня кількості спостережень. У випадку\(1000\) спостережень правило Рису дає\(20\) інтервали замість\(11\) рекомендованого правилом Стерджеса. Для прикладу психологічного тесту, використаного вище, правило Стерджеса рекомендує\(10\) інтервали, тоді як правило Райсу рекомендує\(17\). Зрештою, ми скомпрометовані і вибрали\(13\) інтервали для Figure,\(\PageIndex{1}\) щоб створити гістограму, яка здавалася найбільш чіткою. Найкраща порада - експериментувати з різними варіантами ширини та вибирати гістограму відповідно до того, наскільки добре вона передає форму розподілу.

Щоб надати досвід побудови гістограм, ми розробили інтерактивну демонстрацію. Демонстрація виявляє наслідки різних варіантів ширини бункера та нижньої межі для першого інтервалу.

Інтерактивна гістограма