1.10: Дистрибутиви

Last updated

Oct 28, 2022
Save as PDF
- 1.9: Вимірювання
- 1.11: Позначення підсумовування

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте «розподіл»
Інтерпретувати розподіл частот
Розрізняють розподіл частот і розподіл ймовірностей
Побудувати згрупований розподіл частот для неперервної змінної
Визначте перекіс розподілу
Визначте бімодальні, лептокуртіческіе та плетикуртіческіе розподіли

Розподіли дискретних змінних

Нещодавно придбаний мішок Plain M&M's містив цукерки шести різних кольорів. Швидкий підрахунок показав, що існують $55$ M&M: $17$ коричневий, $18$ червоний, $7$ жовтий, $7$ зелений, $2$ синій та $4$ помаранчевий. Ці підрахунки наведені нижче в табл $\PageIndex{1}$ .

Таблиця $\PageIndex{1}$ : Частоти в сумці M&M
Колір	Частота
Коричневий	17
Червоний	18
Жовтий	7
Зелений	7
Синій	2
Помаранчевий	4

Ця таблиця називається таблицею частот і описує розподіл колірних частот M&M. Не дивно, що такий вид розподілу називається частотним розподілом. Часто частотний розподіл показано графічно, як на малюнку $\PageIndex{1}$ .

альт

Малюнок $\PageIndex{1}$ : Розподіл $55$ M&M.

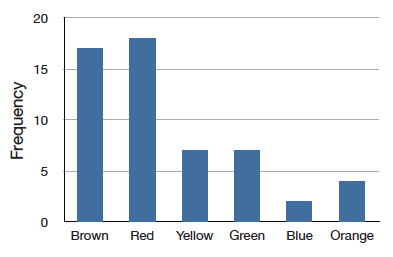
Розподіл, показаний на малюнку, $\PageIndex{1}$ стосується лише моєї однієї сумки M&M. Можливо, вам буде цікаво розподіл кольорів для всіх M&M. Виробник M&M's надає деяку інформацію з цього приводу, але вони не говорять нам точно, скільки M&M кожного кольору вони коли-небудь виробляли. Натомість вони повідомляють про пропорції, а не частоти. На малюнку $\PageIndex{2}$ показані ці пропорції. Оскільки кожен M&M є одним із шести знайомих кольорів, шість пропорцій, показаних на малюнку, додають до одного. Ми називаємо Рисунок $\PageIndex{2}$ розподілом ймовірностей, тому що якщо ви вибираєте M&M випадковим чином, ймовірність отримання, скажімо, коричневого M&M дорівнює частці M & M, які є коричневими ( $0.30$ ).

альт — Малюнок $\PageIndex{2}$ : Розподіл всіх M&M.

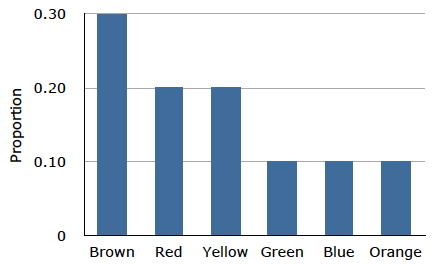
Зверніть увагу, що розподіли на малюнках $\PageIndex{1}$ і $\PageIndex{2}$ не ідентичні. Малюнок $\PageIndex{1}$ зображує розподіл у зразку $55$ M&M. $\PageIndex{2}$ На малюнку показані пропорції для всіх M&M. Шансові фактори, що стосуються машин, що використовуються виробником, вводять випадкові зміни в різні випускаються мішки. Деякі сумки матимуть розподіл кольорів, близький до малюнка $\PageIndex{2}$ ; інші будуть далі.

Безперервні змінні

Використовувана в даному прикладі змінна «color of M&M» є дискретною змінною, а її розподіл ще називають дискретним. Давайте тепер розширимо поняття розподілу на неперервні змінні. Дані, наведені в таблиці $\PageIndex{2}$ , - це час, який знадобився одному з нас (DL), щоб навести курсор миші на невелику ціль у серії $20$ випробувань. Часи сортуються від найкоротшого до найдовшого. Змінна «час реагування» є безперервною змінною. З часом, виміряним точно (до багатьох знаків після коми), не очікується, що два рази відгуку будуть однаковими. Вимірювання часу в мілісекундах (тисячних частках секунди) часто досить точне, щоб наблизити безперервну змінну в психології. Як ви можете бачити в таблиці $\PageIndex{2}$ , вимірювання відповідей DL таким чином не виробляло раз, два з яких були однаковими. В результаті розподіл частот був би неінформативним: він складатиметься з $20$ часів експерименту, кожен з частотою $1$ .

Таблиця $\PageIndex{2}$ : Час відгуку
568	720
577	728
581	729
640	777
641	808
645	824
657	825
673	865
696	875
703	1007

Рішенням цієї проблеми є створення згрупованого частотного розподілу. У згрупованому розподілі частот бали, що потрапляють у різні діапазони, зведені в таблицю. Таблиця $\PageIndex{3}$ показує згрупований розподіл частот за ці $20$ часи.

Таблиця $\PageIndex{3}$ : Згрупований розподіл частот
Діапазон	Частота
500-600	3
600-700	6
700-800	5
800-900	5
900-1000	0
1000-1100	1

Згруповані частотні розподіли можуть бути зображені графічно. $\PageIndex{3}$ На малюнку показано графічне зображення частотного розподілу в табл $\PageIndex{3}$ . Такий вид графіка називається гістограмою. Пізніша глава містить цілий розділ, присвячений гістограмам.

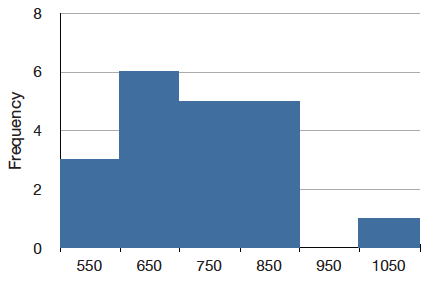
Щільність ймовірності

Гістограма на малюнку $\PageIndex{3}$ зображує лише $20$ часи ДЛ в одному експерименті, який він виконав. Щоб уявити ймовірність, пов'язану з довільним рухом (яке може зайняти будь-яку позитивну кількість часу), ми повинні представляти всі ці потенційні часи відразу. Для цього будуємо розподіл для безперервної змінної часу. Розподіли для неперервних змінних називаються неперервними розподілами. Вони також несуть химерну назву щільності ймовірності. Деякі щільності ймовірності мають особливе значення в статистиці. Дуже важливий має форму дзвіночка, і називається нормальним розподілом. Багато природних явищ можна наблизити напрочуд добре цим розподілом. Він послужить для ілюстрації деяких особливостей всіх безперервних дистрибутивів.

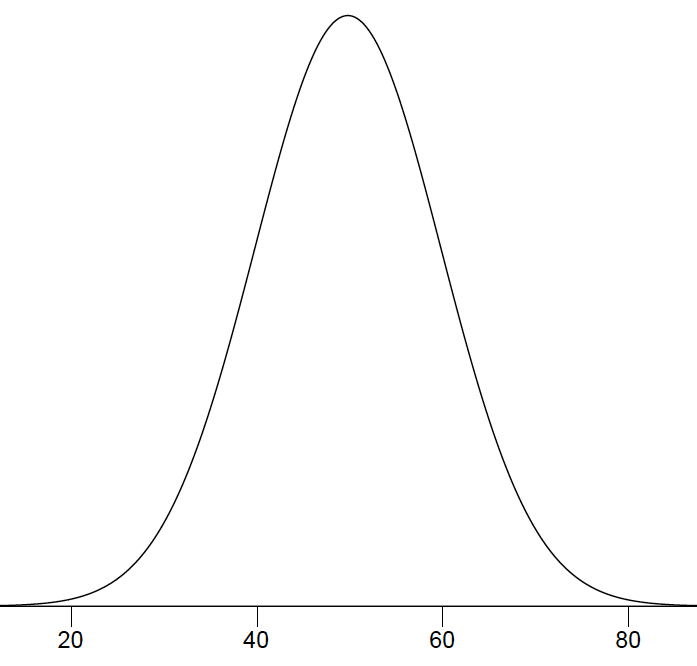
Приклад нормального розподілу показаний на рис $\PageIndex{4}$ . Ви бачите «дзвіночок»? Нормальний розподіл не є справжнім дзвіночком, однак, оскільки лівий і правий кінчики продовжуються на невизначений термін (ми не можемо намалювати їх далі, щоб вони виглядали так, ніби вони зупинилися на нашій діаграмі). $Y$ -вісь у нормальному розподілі представляє «щільність ймовірності». Інтуїтивно він показує ймовірність отримання значень поблизу відповідних точок на $X$ -осі. На малюнку $\PageIndex{4}$ , наприклад, ймовірність спостереження зі значенням поруч $40$ становить приблизно половину ймовірності спостереження зі значенням поруч $50$ . (Для отримання додаткової інформації, будь ласка, зверніться до розділу про звичайні дистрибутиви.)

Хоча цей текст не обговорює поняття щільності ймовірності детально, слід мати на увазі наступні ідеї щодо кривої, яка описує безперервний розподіл (наприклад, нормальний розподіл). По-перше, площа під кривою дорівнює $1$ . По-друге, ймовірність будь-якого точного значення $X$ є $0$ . Нарешті, площа під кривою і обмежена між двома заданими точками на $X$ -осі - це ймовірність того, що число, вибране випадковим чином, потрапить між двома точками. Давайте проілюструємо рухами рук DL. По-перше, ймовірність того, що його рух займе якусь кількість часу, одна! (Ми виключаємо можливість того, що він ніколи не закінчує свій жест.) По-друге, ймовірність того, що його рух займає рівно $598.956432342346576$ мілісекунди, по суті дорівнює нулю. (Ми можемо зробити ймовірність якомога ближче до нуля, зробивши вимірювання часу все більш точним.) Нарешті, припустимо, що ймовірність руху DL займає між $700$ мілісекундами $600$ і становить одну десяту. Тоді безперервний розподіл для можливих часів ДЛ матиме форму, яка розміщує $10\%$ область нижче кривої в області, обмеженій $600$ осі та $700$ на $X$ осі.

Форми розподілів

Розподіли мають різну форму; вони не всі виглядають як звичайний розподіл на малюнку $\PageIndex{4}$ . Наприклад, нормальна щільність ймовірності вище посередині в порівнянні з двома її хвостами. Інші дистрибутиви не повинні мати цю функцію. Існує навіть варіація серед дистрибутивів, які ми називаємо «нормальними». Наприклад, деякі нормальні розподіли більш поширені, ніж показано на малюнку $\PageIndex{4}$ (їх хвости починають потрапляти по $X$ осі далі від середини кривої - наприклад, при $10$ і $90$ якщо намальовано замість малюнка $\PageIndex{4}$ ). Інші менш розправлені (їх хвости можуть наближатися до $X$ $30$ -осі в і $70$ ). Більш детальну інформацію про нормальному розподілі можна знайти в більш пізньому розділі, повністю присвяченому їм.

Розподіл, показаний на малюнку $\PageIndex{4}$ , симетричний; якщо скласти його посередині, обидві сторони будуть ідеально збігатися. $\PageIndex{5}$ На малюнку показано дискретний розподіл балів на тесті з психології. Такий розподіл не симетричний: хвіст в позитивному напрямку простягається далі хвоста в негативну сторону. Кажуть, що розподіл з довшим хвостом, що поширюється в позитивному напрямку, має позитивний перекос. Він також описується як «перекіс вправо».

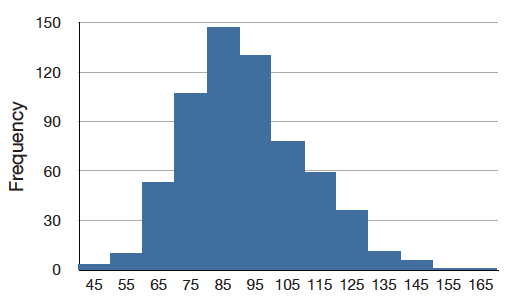
$\PageIndex{6}$ На малюнку показані зарплати гравців вищої ліги бейсболу 1974 року (в тисячах доларів). Цей розподіл має крайній позитивний перекос.

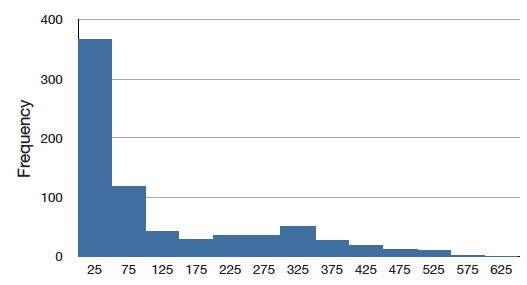
Безперервний розподіл з позитивним перекосом показано на малюнку $\PageIndex{7}$ .

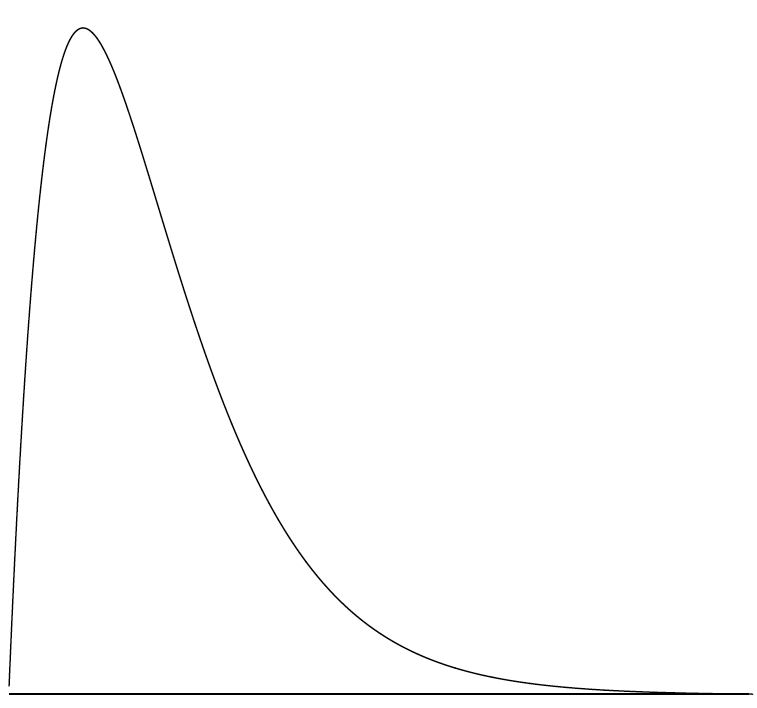
Хоча і рідше, деякі дистрибутиви мають негативний перекіс. $\PageIndex{8}$ На малюнку показані бали за $20$ задачею -point на статистичному іспиті. Так як хвіст розподілу поширюється вліво, то цей розподіл перекошується вліво.

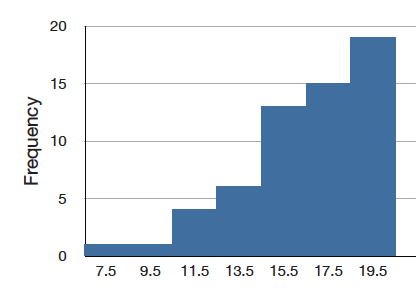
Гістограма на малюнку $\PageIndex{8}$ показує частоти різних балів на питання $20$ -point на статистичному тесті.

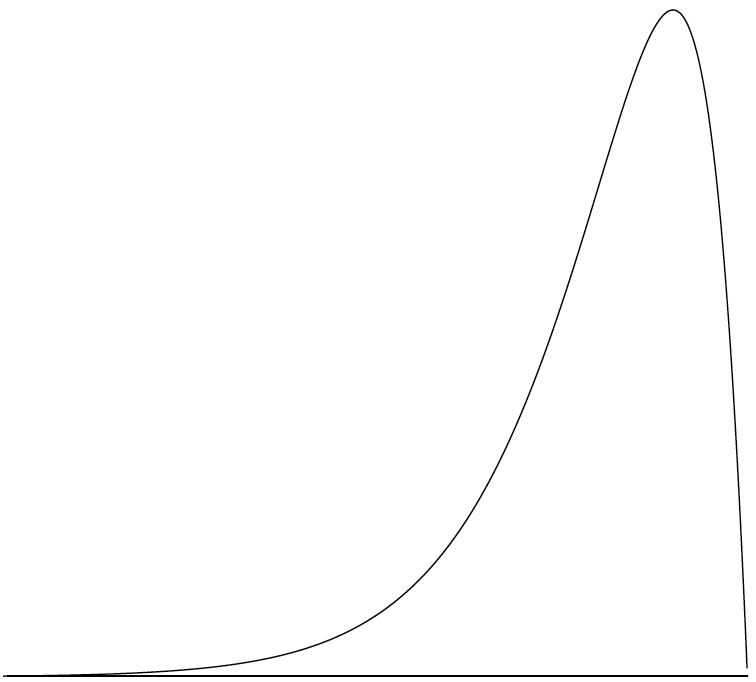
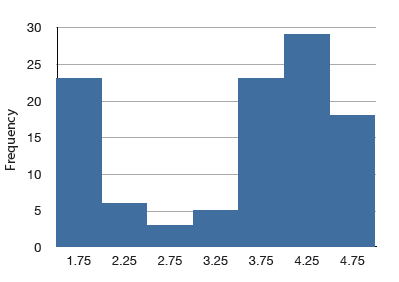
Безперервний розподіл з негативним перекосом показано на малюнку $\PageIndex{9}$ . Показані досі розподіли мають одну окрему високу точку або пік. Розподіл на малюнку $\PageIndex{10}$ має дві чіткі піки. Розподіл з двома піками називається бімодальним розподілом.

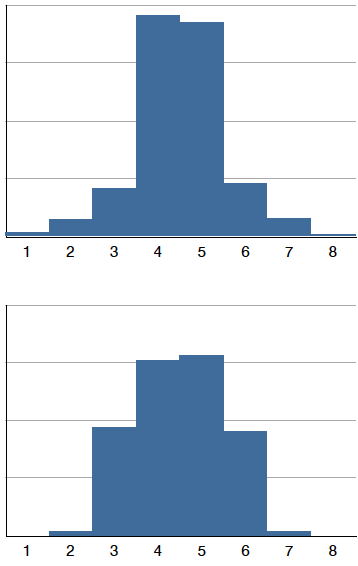
Розподіли також відрізняються один від одного в плані того, наскільки великі або «жирні» їх хвости. $\PageIndex{11}$ На малюнку показані два розподіли, які відрізняються в цьому відношенні. Верхній розподіл має порівняно більше балів у хвостах; його форма називається лептокуртіческой. Нижній розподіл має відносно менше балів у хвостах; його форма називається платикуртіческой.

Автори та атрибуція

Template:Lane
David M. Lane and Heidi Ziemer