2.3: Статистичне мислення
- Page ID
- 88718
Бет Шанс і Аллан Россман
Каліфорнійський політехнічний державний університет, Сан-Луїс-Обіспо
Оскільки наше суспільство все частіше закликає до прийняття рішень на основі доказів, важливо враховувати, як і коли ми можемо зробити достовірні висновки з даних. Цей модуль буде використовувати чотири останні дослідження, щоб виділити ключові елементи статистичного дослідження.
цілі навчання
- Визначте основні елементи статистичного дослідження.
- Охарактеризуйте роль p-значень та довірчих інтервалів у статистичному висновку.
- Охарактеризуйте роль випадкової вибірки в узагальнюючих висновках від вибірки до популяції.
- Охарактеризуйте роль випадкового присвоєння у формуванні причинно-наслідкових висновків.
- Критика статистичних досліджень.
Вступ
Чи справді вживання кави збільшує тривалість життя? Недавнє дослідження (Freedman, Park, Abnet, Hollenbeck, & Sinha, 2012) показало, що чоловіки, які пили щонайменше шість чашок кави на день, мали 10% нижчий шанс померти (жінки на 15% нижче), ніж ті, хто не пив жодної. Чи означає це, що ви повинні підібрати або збільшити власну звичку кави?
Сучасне суспільство захлинулося такими дослідженнями, як це; ви можете прочитати про кілька таких досліджень в новині кожен день. Більш того, дані рясніють всюди в сучасному житті. Проведення такого дослідження добре, і інтерпретація результатів таких досліджень добре для прийняття обґрунтованих рішень або постановки політики, вимагає розуміння основних ідей статистики, науки отримання розуміння з даних. Замість того, щоб покладатися на анекдот і інтуїцію, статистика дозволяє систематично вивчати цікаві явища.

Ключовими компонентами статистичного дослідження є:
- Планування дослідження: Почніть з того, щоб поставити тестоване дослідницьке питання та вирішити, як збирати дані. Наприклад, як довго тривав період дослідження кави? Скільки людей було набрано для навчання, як їх набирали і звідки? Скільки їм було років? Які ще змінні були записані про людей, такі як звички куріння, на всеосяжних анкетах способу життя? Чи були внесені зміни до кавових звичок учасників під час дослідження?
- Вивчення даних: Які є відповідні способи вивчення даних? Які графіки актуальні, і що вони розкривають? Яку описову статистику можна розрахувати, щоб узагальнити відповідні аспекти даних, і що вони виявляють? Які закономірності ви бачите в даних? Чи існують окремі спостереження, які відхиляються від загальної закономірності, і що вони виявляють? Наприклад, у дослідженні кави чи відрізнялися пропорції, коли ми порівнювали курців з некурящими?
- Висновок з даних: Які дійсні статистичні методи для проведення висновків «поза» зібраними вами даними? У дослідженні кави, чи є зниження ризику смерті на 10% - 15%, що могло статися просто випадково?
- Роблячи висновки: Виходячи з того, що ви дізналися зі своїх даних, які висновки ви можете зробити? Як ви думаєте, до кого ці висновки відносяться? (Чи були люди в каві дослідження старшими? Здоровий? Жити в містах?) Чи можете ви зробити причинно-наслідковий висновок про лікування? (Чи кажуть вчені зараз, що вживання кави є причиною зниження ризику смерті?)
Зверніть увагу, що числовий аналіз («хрускіт чисел» на комп'ютері) включає лише невелику частину загального статистичного дослідження. У цьому модулі ви побачите, як ми можемо відповісти на деякі з цих питань та які питання ви повинні задати щодо будь-якого статистичного дослідження, про яке ви читаєте.
Розподільне мислення
Коли дані збираються для вирішення певного питання, важливим першим кроком є продумування значущих способів організації та вивчення даних. Найголовніший принцип статистики полягає в тому, що дані змінюються. Шаблон цієї варіації має вирішальне значення для захоплення та розуміння. Часто ретельне подання даних буде вирішувати багато питань дослідження, не вимагаючи більш складного аналізу. Однак він може вказувати на додаткові питання, які потрібно розглянути більш детально.
Приклад 1: Дослідники досліджували, чи написані брошури про рак на належному рівні для читання та розуміння онкологічними хворими (Short, Moriarty, & Cooley, 1995). Тести здатності до читання були надані 63 пацієнтам. Крім того, рівень читабельності був визначений для вибірки з 30 брошур, виходячи з таких характеристик, як довжина слів і пропозицій в брошурі. Результати, повідомлені в розрізі рівнів оцінок, відображаються в таблиці 1.

Ці дві змінні розкривають два основні аспекти статистичного мислення:
- Дані різняться. Більш конкретно, значення змінної (наприклад, рівень читання хворого на рак або рівень читабельності брошури про рак) варіюються.
- Аналізуючи закономірність варіації, звану розподілом змінної, часто виявляє інсайти.
Вирішення дослідницького питання про те, чи написані брошури раку на відповідних рівнях для хворих на рак, вимагає порівняння двох розподілів. Наївне порівняння може зосередитися лише на центрах розподілів. Обидва медіани виявляються дев'ятим класом, але розглядаючи лише медіани, ігнорує мінливість і загальні розподіли цих даних. Більш освітлюючим підходом є порівняння цілих розподілів, наприклад, з графіком, як на малюнку 1.
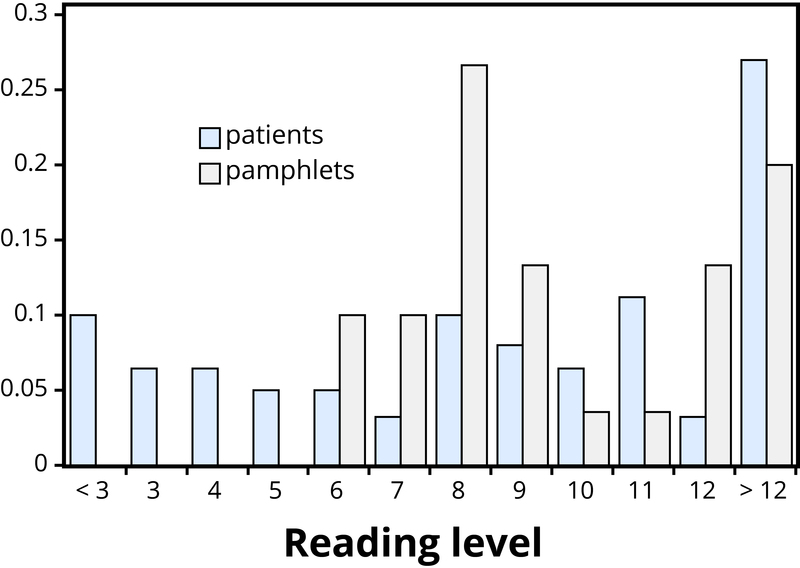
Малюнок 2.3.1 дає зрозуміти, що два дистрибутиви взагалі погано вирівняні. Найбільш кричуща невідповідність полягає в тому, що багато пацієнтів (17/63, або 27%, якщо бути точними) мають рівень читання нижче рівня найбільш читабельної брошури. Цим пацієнтам знадобиться допомога, щоб зрозуміти інформацію, надану в брошурах про рак. Зверніть увагу, що цей висновок випливає з розгляду розподілів в цілому, а не просто мір центру або мінливості, і що графік контрастує ці розподіли більш відразу, ніж таблиці частот.
Статистичне значення
Навіть коли ми знаходимо закономірності в даних, часто все ще існує невизначеність у різних аспектах даних. Наприклад, можуть бути можливі помилки вимірювання (навіть ваша власна температура тіла може коливатися майже на 1° F протягом дня). Або ми можемо мати лише «знімок» спостережень з більш довгострокового процесу або лише невелика підмножина індивідів із зацікавленої популяції. У таких випадках, як ми можемо визначити, чи закономірності, які ми бачимо в нашому невеликому наборі даних, є переконливим свідченням систематичного явища в більшому процесі чи популяції?
Приклад 2: У дослідженні, повідомленому у випуску Nature у листопаді 2007 року, дослідники досліджували, чи враховують довербальні немовлята дії людини щодо інших, оцінюючи цю особу як привабливу чи аверсивну (Hamlin, Wynn, & Bloom, 2007). В одному з компонентів дослідження 10-місячним немовлятам був показаний характер «альпініста» (шматок дерева з наклеєними на нього «гуглими» очима), який не міг піднятися на пагорб за дві спроби. Потім немовлятам показали два сценарії наступної спроби альпініста, один, де альпініста підштовхнув на вершину пагорба іншим персонажем («помічником»), і один, де альпініста відсунув назад з пагорба іншим персонажем («перешкодою»). Немовляти по черзі показували ці два сценарії кілька разів. Потім немовляти подарували два шматки дерева (що представляють помічника і перешкоджають персонажам) і попросили вибрати один, з яким пограти. Дослідники виявили, що з 16 немовлят, які зробили чіткий вибір, 14 вирішили пограти з іграшкою-помічником.

Одне з можливих пояснень цього чіткого результату більшості полягає в тому, що допоміжна поведінка однієї іграшки збільшує ймовірність вибору немовлят цієї іграшки. Але чи є інші можливі пояснення? А як щодо кольору іграшки? Ну, перш ніж збирати дані, дослідники влаштували так, щоб кожен колір і форма (червоний квадрат і синє коло) бачили однакову кількість немовлят. А може, у немовлят були правосторонні нахили і так вибирали якусь іграшку ближче до правої руки? Ну, перш ніж збирати дані, дослідники влаштували його так, щоб половина немовлят побачила іграшку помічника праворуч і половину зліва. Або, може бути, форми цих дерев'яних символів (квадрат, трикутник, коло) мали ефект? Можливо, але знову ж таки, дослідники контролювали це, обертаючи, яка форма була іграшкою-помічником, іграшкою-перешкодою та альпіністом. При розробці експериментів важливо контролювати якомога більше змінних, які можуть вплинути на відповіді, наскільки це можливо.
Починає здаватися, що дослідники врахували всі інші правдоподібні пояснення. Але є ще один важливий аспект, який неможливо контролювати - якщо ми знову проведемо дослідження з цими 16 немовлятами, вони могли б не зробити той самий вибір. Іншими словами, є певна випадковість, властива їх процесу вибору. Можливо, кожна немовля взагалі не мала справжніх переваг, і це була просто «випадкова удача», яка призвела до того, що 14 немовлят вибирали допоміжну іграшку. Хоча цей випадковий компонент не можна контролювати, ми можемо застосувати модель ймовірності для дослідження закономірності результатів, які мали б відбутися в довгостроковій перспективі, якби випадковий шанс був єдиним фактором.
Якщо немовлята з однаковою ймовірністю вибирали між двома іграшками, то кожна дитина мала 50% шансів вибрати іграшку помічника. Це ніби кожен немовля кинув монетку, і якщо він приземлився головами, немовля підбирав допоміжну іграшку. Отже, якби ми кинули монету 16 разів, чи могла б вона приземлитися головами 14 разів? Звичайно, це можливо, але виявляється дуже малоймовірним. Отримання 14 (або більше) голів у 16 киданнях приблизно так само ймовірно, як кидання монети і отримання 9 голів поспіль. Цю ймовірність називають p-значенням. Значення p говорить вам, як часто випадковий процес дасть результат принаймні такий екстремальний, як те, що було знайдено в фактичному дослідженні, припускаючи, що не було нічого іншого, ніж випадковий шанс у грі. Отже, якщо припустити, що кожен немовля вибирав однаково, то ймовірність того, що 14 і більше з 16 немовлят виберуть допоміжну іграшку, виявляється 0,0021. У нас є лише дві логічні можливості: або немовлята мають справжню перевагу іграшки-помічника, або немовлята не мають переваг (50/50), і результат, який відбувся б лише 2 рази за 1000 ітерацій, стався в цьому дослідженні. Оскільки це p-значення 0,0021 досить невелике, ми робимо висновок, що дослідження дає дуже вагомі докази того, що ці немовлята мають справжню перевагу іграшці-помічнику. Ми часто порівнюємо p-значення з деяким значенням відсічення (називається рівнем значущості, зазвичай близько 0,05). Якщо p-значення менше, ніж це значення відсікання, то ми відкидаємо гіпотезу, що тут грав лише випадковий шанс. У цьому випадку ці дослідники прийдуть до висновку, що значно більше половини немовлят у дослідженні обрали допоміжну іграшку, даючи вагомі докази справжньої переваги іграшки з допоміжною поведінкою.
Узагальнюваність

Одне з обмежень попереднього дослідження полягає в тому, що висновок стосується лише 16 немовлят у дослідженні. Ми не знаємо багато про те, як були відібрані ці 16 немовлят. Припустимо, ми хочемо виділити підмножину індивідів (вибірку) з набагато більшої групи індивідів (популяції) таким чином, щоб висновки з вибірки можна було узагальнити до більшої популяції. Це питання, з яким стикаються опитувальники щодня.
Приклад 3: Загальне соціальне опитування (GSS) - це опитування щодо соціальних тенденцій, яке проводиться щороку в Сполучених Штатах. Виходячи з вибірки з приблизно 2000 дорослих американців, дослідники заявляють про те, який відсоток населення США вважає себе «ліберальними», який відсоток вважає себе «щасливими», який відсоток відчуває себе «поспішним» у своєму повсякденному житті та багато інших питань. Ключ до висунення цих тверджень щодо більшої чисельності населення всіх американських дорослих полягає в тому, як вибирається вибірка. Мета полягає в тому, щоб вибрати вибірку, яка є репрезентативною для населення, і поширеним способом досягнення цієї мети є вибір випадкової вибірки, яка дає кожному члену населення рівні шанси бути відібраним для вибірки. У найпростішій формі випадкова вибірка передбачає нумерацію кожного члена населення, а потім використання комп'ютера для випадкового вибору підмножини для обстеження. Більшість опитувань не працюють саме так, але вони використовують методи вибірки, засновані на ймовірності, для вибору осіб з національно репрезентативних панелей.
У 2004 році GSS повідомила, що 817 з 977 респондентів (або 83,6%) вказали, що вони завжди або іноді відчувають себе поспішними. Це явна більшість, але нам знову потрібно розглянути варіації через випадкову вибірку. На щастя, ми можемо використовувати ту саму модель ймовірності, яку ми зробили в попередньому прикладі, щоб дослідити ймовірний розмір цієї помилки. (Зверніть увагу, ми можемо використовувати модель кидання монети, коли фактичний розмір населення набагато, набагато більше, ніж розмір вибірки, оскільки тоді ми все ще можемо вважати ймовірність бути однаковою для кожної людини у вибірці.) Ця модель ймовірності передбачає, що результат вибірки буде знаходитися в межах 3 процентних пунктів від значення популяції (приблизно 1 над квадратним коренем розміру вибірки, похибка). Статист зробив би висновок, з 95% впевненістю, що між 80,6% і 86,6% всіх дорослих американців у 2004 році відповіли б, що вони іноді або завжди відчувають себе поспішними.
Ключ до похибки полягає в тому, що коли ми використовуємо метод вибірки ймовірності, ми можемо пред'явити претензії про те, як часто (у довгостроковій перспективі, з повторною випадковою вибіркою) результат вибірки потраплятиме на певну відстань від невідомого значення популяції випадково (тобто випадковою варіацією вибірки) поодинці. І навпаки, невипадкові зразки часто підозрюються в упередженості, тобто метод вибірки систематично надмірно представляє деякі верстви населення та недостатньо представляє інших. Нам також все ще потрібно враховувати інші джерела упередженості, такі як люди, які не відповідають чесно. Ці джерела похибки не вимірюються похибкою.
Причинно-наслідкові висновки
У багатьох дослідженнях первинне питання, що цікавить, стосується відмінностей між групами. Тоді постає питання, як формувалися групи (наприклад, відбір людей, які вже п'ють каву проти тих, хто цього не робить). У деяких дослідженнях дослідники активно формують самі групи. Але тоді у нас виникає подібне питання - чи можуть будь-які відмінності, які ми спостерігаємо в групах, бути артефактом цього процесу формування групи? Або, можливо, різниця, яку ми спостерігаємо в групах, настільки велика, що ми можемо скинути «випадковість» у процесі формування групи як розумне пояснення того, що ми знаходимо?
Приклад 4: Психологічне дослідження досліджувало, чи схильні люди проявляти більше творчості, коли вони думають про внутрішні або зовнішні мотивації (Ramsey & Schafer, 2002, на основі дослідження Amabile, 1985). Суб'єктами були 47 осіб з великим досвідом роботи з творчим письмом. Суб'єкти починали з відповіді на запитання опитування або про внутрішні мотивації до письма (наприклад, задоволення від самовираження), або про зовнішні мотивації (наприклад, суспільне визнання). Потім всім предметам було доручено написати хайку, а ці вірші оцінювали на творчість колегією суддів. Дослідники заздалегідь припускали, що суб'єкти, які думали про внутрішні мотивації, виявлять більше творчості, ніж суб'єкти, які думали про зовнішні мотивації. Бали творчості з 47 предметів у цьому дослідженні відображаються на малюнку 2, де вищі бали вказують на більше творчості.
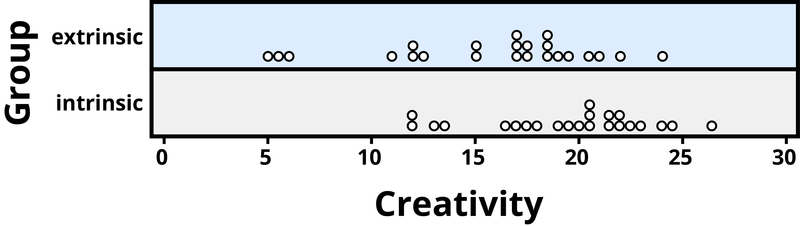
У цьому прикладі ключове питання полягає в тому, чи впливає тип мотивації на результати творчості. Зокрема, чи мають суб'єкти, яких запитували про внутрішні мотивації, мають вищі показники творчості, ніж суб'єкти, яких запитували про зовнішні мотивації?
Малюнок 2.3.2 показує, що обидві групи мотивації бачили значну мінливість балів творчості, і ці бали мають значне перекриття між групами. Іншими словами, це, звичайно, не завжди так, що ті, хто має зовнішні мотивації, мають вищу творчість, ніж ті, хто має внутрішні мотивації, але все ж може бути статистична тенденція в цьому напрямку. (Психолог Кіт Станович (2013) посилається на труднощі людей з мисленням про такі ймовірнісні тенденції, як «ахіллесова п'ята людського пізнання».)
Середній бал творчості становить 19,88 для внутрішньої групи, порівняно з 15,74 для зовнішньої групи, що підтримує здогадки дослідників. Однак порівняння лише засобів двох груп не враховує варіативність балів творчості в групах. Ми можемо виміряти мінливість за допомогою статистики, використовуючи, наприклад, стандартне відхилення: 5,25 для зовнішньої групи та 4,40 для внутрішньої групи. Стандартні відхилення говорять нам, що більшість балів творчості знаходяться в межах приблизно 5 балів від середнього балу в кожній групі. Ми бачимо, що середній бал для внутрішньої групи лежить в межах одного стандартного відхилення від середнього балу для зовнішньої групи. Отже, хоча існує тенденція до того, щоб бали творчості були вищими у внутрішній групі, в середньому різниця не надзвичайно велика.
Ми знову хочемо розглянути можливі пояснення цієї різниці. У дослідженні брали участь лише особи з великим творчим досвідом письма. Хоча це обмежує населення, до якого ми можемо узагальнити, це не пояснює, чому середній показник творчості був трохи більшим для внутрішньої групи, ніж для зовнішньої групи. Може бути, жінки, як правило, отримують вищі бали творчості? Ось де нам потрібно зосередитись на тому, як особи були призначені до груп мотивації. Якби тільки жінки були в групі внутрішньої мотивації і тільки чоловіки в зовнішній групі, то це представляло б проблему, тому що ми б не знали, чи внутрішня група зробила краще через інший тип мотивації або тому, що вони були жінками. Однак дослідники оберігалися від такої проблеми, випадковим чином привласнюючи людей до груп мотивації. Як і гортати монету, кожна людина так само ймовірно була призначена для будь-якого типу мотивації. Чому це корисно? Оскільки це випадкове призначення має тенденцію збалансувати всі змінні, пов'язані з творчістю, про які ми можемо думати, і навіть ті, про які ми не думаємо заздалегідь, між двома групами. Таким чином, ми повинні мати подібний чоловічий і жіночий поділ між двома групами; ми повинні мати подібний віковий розподіл між двома групами; ми повинні мати подібний розподіл освіти між двома групами; і так далі. Випадкове присвоєння повинно виробляти групи, максимально схожі за винятком типу мотивації, що імовірно виключає всі ці інші змінні як можливі пояснення спостережуваної тенденції до більш високих балів у внутрішній групі.
Але чи завжди це працює? Ні, тому за «удачею розіграшу» групи можуть трохи відрізнятися до відповіді на опитування мотивації. Отже, питання полягає в тому, чи можливо, що невдале випадкове призначення відповідає за спостережувану різницю в балах творчості між групами? Іншими словами, припустимо, що вірш кожної людини збирався отримати однаковий бал творчості незалежно від того, до якої групи вони були приписані, що тип мотивації жодним чином не вплинув на їхню оцінку. Тоді як часто сам процес випадкового призначення призведе до різниці в середніх балах творчості, як великі (або більші), ніж 19,88 - 15,74 = 4,14 балів?
Ми знову хочемо застосувати до моделі ймовірності, щоб наблизити p-значення, але цього разу модель буде трохи іншою. Подумайте про те, щоб написати оцінки творчості кожного на індексній картці, перетасувати індексні картки, а потім роздавати 23 до групи зовнішньої мотивації та 24 до внутрішньої групи мотивації, і знайти різницю в групі означає. Ми (ще краще, комп'ютер) можемо повторювати цей процес знову і знову, щоб побачити, як часто, коли бали не змінюються, випадкове присвоєння призводить до різниці в засобах принаймні стільки ж, скільки 4.41. На малюнку 2.3.3 показані результати 1,000 таких гіпотетичних випадкових завдань для цих балів.
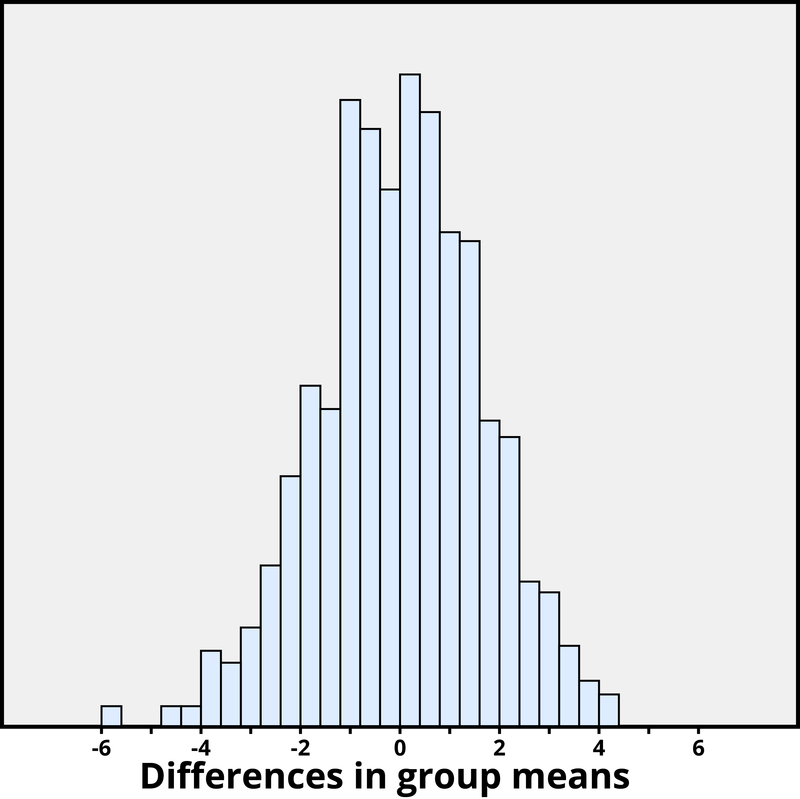
Лише 2 з 1000 змодельованих випадкових завдань дали різницю в групових середніх 4.41 або більше. Іншими словами, приблизне p-значення дорівнює 2/1000 = 0,002. Це невелике p-значення вказує на те, що було б дуже дивно, що лише процес випадкового присвоєння виробляє таку велику різницю в групових засобах. Тому, як і у прикладі 2, ми маємо вагомі докази того, що зосередження уваги на внутрішніх мотиваціях має тенденцію до збільшення балів творчості порівняно з думкою про зовнішні мотивації.
Зверніть увагу, що попереднє твердження передбачає причинно-наслідковий зв'язок між мотивацією та оцінкою творчості; чи виправданий такий сильний висновок? Так, через випадкового призначення, використаного в дослідженні. Це повинно було збалансувати будь-які інші змінні між двома групами, так що тепер, коли мале p-значення переконує нас, що вище середнє значення у внутрішній групі було не просто збігом, єдине розумне пояснення залишилося - це різниця у типі мотивації. Чи можемо ми узагальнити цей висновок всім? Не обов'язково - ми могли б обережно узагальнити цей висновок особам, які мають великий досвід творчого письма, подібних людям у цьому дослідженні, але ми все одно хотіли б дізнатися більше про те, як ці особи були обрані для участі.
Висновок
Статистичне мислення передбачає ретельне проектування дослідження для збору значущих даних для відповіді на цілеспрямоване дослідницьке питання, детальний аналіз закономірностей у даних та складання висновків, що виходять за рамки спостережуваних даних. Випадкова вибірка має першорядне значення для узагальнення результатів нашої вибірки до більшої популяції, а випадкове призначення є ключовим для отримання причинно-наслідкових висновків. При обох видах випадковості моделі ймовірності допомагають нам оцінити, скільки випадкових варіацій ми можемо очікувати в наших результатах, щоб визначити, чи можуть наші результати статися випадково поодинці та оцінити похибку.
Отже, де це залишає нас стосовно дослідження кави, згаданого на початку цього модуля? Ми можемо відповісти на багато питань:
- Це було 14-річне дослідження, проведене дослідниками Національного інституту раку.
- Результати були опубліковані в червневому номері журналу New England Journal of Medicine, шанованого, рецензованого журналу.
- У дослідженні розглянуто кавові звички понад 402 000 людей у віці від 50 до 71 років з шести штатів та двох мегаполісів. Ті, хто хворіє на рак, серцеві захворювання та інсульт, були виключені на початку дослідження. Споживання кави оцінювали один раз на початку дослідження.
- Під час дослідження загинуло близько 52 000 чоловік.
- Люди, які пили від двох до п'яти чашок кави щодня, також показали менший ризик, але кількість зменшення збільшилася для тих, хто п'є шість і більше чашок.
- Розміри вибірки були досить великими, і тому p-значення досить малі, хоча відсоток зниження ризику не був надзвичайно великим (падіння з 12% шансу приблизно до 10% - 11%).
- Чи була кава кофеїном або без кофеїну, здається, не впливає на результати.
- Це було спостережливе дослідження, тому ніяких причинно-наслідкових висновків між питтям кави та збільшенням довголіття не можна робити, всупереч враженню, яке передають багато заголовків новин про це дослідження. Зокрема, можливо, що ті, хто страждає хронічними захворюваннями, не схильні пити каву.
Це дослідження потрібно переглянути в більшому контексті подібних досліджень та узгодженості результатів у дослідженнях, з постійною обережністю, що це не був рандомізований експеримент. У той час як статистичний аналіз все ще може «пристосуватися» для інших потенційних заплутаних змінних, ми ще не переконані, що дослідники визначили їх усі або повністю ізолювали, чому це зниження ризику смерті очевидно. Дослідники тепер можуть взяти висновки цього дослідження та розробити більш цілеспрямовані дослідження, які стосуються нових питань.
Зовнішні ресурси
- Додатки: Інтерактивні веб-аплети для викладання та вивчення статистики включають збір на
- http://www.rossmanchance.com/applets/
- P-цінність феєрії
- Web: Міжвузівський консорціум політичних та соціальних досліджень
- http://www.icpsr.umich.edu/index.html
- Web: Консорціум для просування статистики бакалаврату
- https://www.causeweb.org/
Питання для обговорення
- Знайдіть недавню дослідницьку статтю у вашій галузі та дайте відповідь на наступне: Яке було первинне дослідницьке питання? Як були відібрані особи для участі в дослідженні? Чи були надані підсумкові результати? Наскільки вагомі докази, представлені на користь чи проти дослідницького питання? Чи використовувалося випадкове призначення? Узагальнити основні висновки з дослідження, розглядаючи питання статистичної значущості, статистичної достовірності, узагальнюваності та причинно-наслідкового характеру. Чи згодні ви з висновками, зробленими в результаті цього дослідження, на основі дизайну дослідження та представлених результатів?
- Чи доцільно використовувати випадкову вибірку з 1,000 осіб, щоб зробити висновки про всіх дорослих США? Поясніть, чому чи чому ні.
Лексика
- Причинно-наслідковий
- Пов'язані з тим, чи ми говоримо, що одна змінна викликає зміни в іншій змінній, в порівнянні з іншими змінними, які можуть бути пов'язані з цими двома змінними.
- Довірчий інтервал
- Інтервал правдоподібних значень для параметра популяції; інтервал значень у межах похибки статистики.
- Дистрибуція
- Схема варіації даних.
- Узагальнюваність
- Пов'язано з тим, чи можна узагальнити результати вибірки до більшої популяції.
- Похибка
- Очікувана величина випадкових варіацій у статистиці; часто визначається для 95% рівня довіри.
- Параметр
- Числовий результат, що підсумовує сукупність (наприклад, середнє значення, пропорція).
- Чисельність населення
- Більша колекція людей, до яких ми хотіли б узагальнити наші результати.
- P-значення
- Імовірність спостереження конкретного результату у вибірці, або більш екстремальної, під здогадкою про більшу сукупність або процес.
- Випадкове призначення
- Використання методу, заснованого на ймовірності, для поділу зразка на групи лікування.
- Випадкова вибірка
- Використання методу, заснованого на ймовірності, для вибору підмножини індивідів для вибірки з популяції.
- Зразок
- Збір осіб, про яких ми збираємо дані.
- Статистика
- Числовий результат обчислюється за зразком (наприклад, середнє значення, пропорція).
- Статистична значимість
- Результат є статистично значущим, якщо він навряд чи виникне випадково поодинці.
Посилання
- Амабіле, Т. Мотивація та креативність: Вплив мотиваційної орієнтації на творчих письменників. Журнал особистості та соціальної психології, 48 (2), 393—399.
- Фрідман, Н.Д., Парк, Ю., Абнет, К., Холленбек, А.Р., і Сінха, Р. (2012). Асоціація пиття кави із загальною та причинно-специфічною смертністю. Медичний журнал Нової Англії, 366, 1891—1904.
- Хамлін, Дж. К., Вінн, К., & Блум, П. (2007). Соціальна оцінка довербальних немовлят. Природа, 452 (22), 557—560.
- Ремсі, Ф., & Шафер, Д. (2002). Статистична лексика: Курс з методів аналізу даних. Белмонт, Каліфорнія: Даксбері.
- Короткий, Т., Моріарті, Х., & Кулі, М.Е. (1995). Читабельність навчальних матеріалів для хворих на рак. Журнал статистики освіти, 3 (2).
- Станович К. Як правильно думати про психологію (10-е видання). Верхня річка Сідло, Нью-Джерсі: Пірсон.