5.5.3: Сили, індуковані хвилями

Наведені вище рівняння описують хвильові випромінювальні напруги, що діють у вертикальній площині води. Горизонтальні градієнти в радіаційних напруженнях породжують чисту хвилю індуковану силу на воду в певному напрямку.

Малюнок 5.31: Сили, індуковані хвилею. Збільшення транспортування імпульсу (збільшення радіаційного напруження) в$x$ - або$y$ -напрямку еквівалентно втраті імпульсу, отже, до надання протилежної сили на водойму.

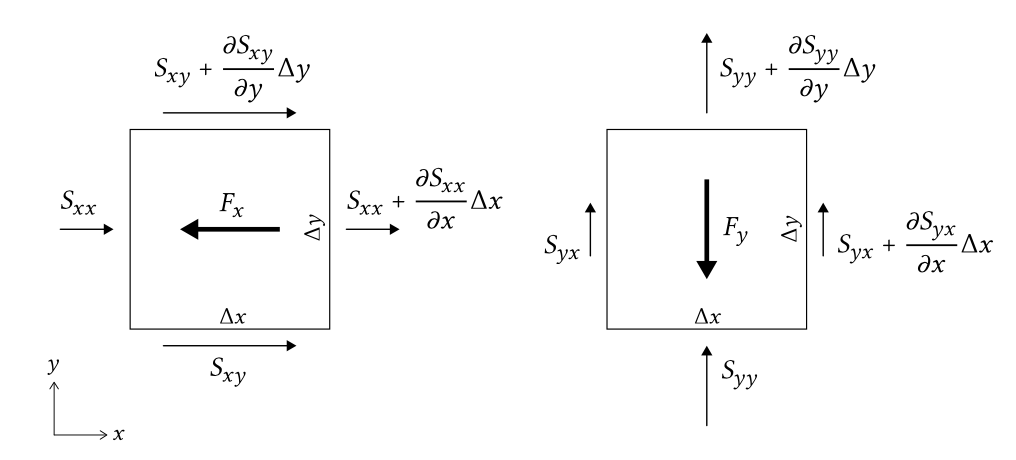
Чиста сила в$x$ -напрямку описується (рис.5.31):

$$F_x = -\left (\dfrac{\partial S_{xx}}{\partial x} + \dfrac{\partial S_{xy}}{\partial y} \right )\label{eq5.5.3.1}$$

де перший член являє собою вплив варіацій в$x$ -спрямованому випромінюванні нормальних напружень, а другий термін - ефект варіацій в$y$ -напрямку напруги зсуву$x$ спрямованого випромінювання.

У прибережній інженерній практиці поширена робота з узбереговими і поперечно-береговими орієнтованими осями. $y$Вісь -визначається паралельно берегової лінії, тоді як$x$ вісь -перпендикулярна береговій лінії. $F_x$це, таким чином, сила в поперечно-береговому напрямку.

Другий (зсувний) термін в еквалайзері. $\ref{eq5.5.3.1}$дорівнює нулю для рівномірної берегової лінії вздовж берега (немає градієнтів у$y$ напрямку -). Тоді у нас є:

$$F_x = -\dfrac{dS_{xx}}{dx} \ \ \text{ for an alongshore uniform coast}$$

У узбереговому напрямку сила становить:

$$F_y = -\left (\dfrac{\partial S_{yy}}{\partial y} + \dfrac{\partial S_{yx}}{\partial x} \right ) \label{eq5.5.3.3}$$

Перший термін в Eq. $\ref{eq5.5.3.3}$може бути ненульовим, якщо градієнти у висоті хвилі відбуваються вздовж узбережжя. Для узбережного рівномірного узбережжя цей термін дорівнює нулю таким, що Eq. $\ref{eq5.5.3.3}$зводиться до:

$$F_y = -\dfrac{dS_{yx}}{dx} \ \ \text{ for an alongshore uniform coast}\label{eq5.5.3.4}$$

Пам'ятайте, що$S_{yx}$ - напруга випромінювання зсуву на площині, перпендикулярній$x$ осі - являє собою$y$ перенесення -імпульсу в$x$ -напрямку. Поперечно-береговий градієнт тут дає чисту силу у$y$ напрямку -.

Варіації радіаційних напружень виникають через зміни$n, E$ або$\theta$. Далі на шельфі хвилі індуковані сили відносно невеликі, але в прибережній зоні великі сили виникають через перетворення хвиль в результаті великих градієнтів в глибині води.

У мілководної області висота хвилі і, отже, енергія хвилі збільшуються до краю зони прибою, звідки висота хвилі та енергія хвилі знову зменшуються. У мілководному районі значення$n$ поступово збільшується від його глибоководної величини$n = 1/2$, до її мілководдя$n = 1$. Кут хвилі$\theta$ поступово зменшується від глибокої води до мілководдя. Сукупний результат - позитивний градієнт$\partial S_{xx}/\partial x$ і офшорна спрямована сила в мілководному районі, а також негативний градієнт$\partial S_{xx} /\partial x$ і наземна спрямована сила в зоні прибою. Розділ 5.5.4 показує, як це призводить до зниження хвилі в області мілководдя та налаштування хвиль у зоні серфінгу. Ми також побачимо, що сила в$y$ -напрямку дорівнює нулю поза зоною прибою, але ненульова в зоні прибою, де вона рухає довгим береговим струмом. Звичайно, він присутній лише в ситуаціях, коли хвилі наближаються до берегової лінії під певним кутом (такий, що є складова орбітальної швидкості хвилі в узбічному напрямку).

Ми висловили інтегровані в глибину хвильові сили з точки зору радіаційних напружень, що досить часто зустрічається в прибережних інженерних додатках. Інші еквівалентні вирази також можна знайти в описі моделей (Intermezzo 5.5).

Intermezzo 5.5 Хвильові сили в рівняннях імпульсу

У рівняннях імпульсу, які усереднені над хвильовим рухом, з'являються хвильові сили. Ці хвильові сили мають два внески: за рахунок коливань тиску та за рахунок передачі імпульсу швидкістю частинок. Вони можуть бути сформульовані з точки зору радіаційних напружень (як в екв. $\ref{eq5.5.3.1}$-Ек. $\ref{eq5.5.3.4}$) або вони можуть еквівалентно виражатися в терміні хвильового орбітального руху і хвильового тиску. В останньому випадку хвильові сили в трьох вимірах можуть виражатися у вигляді:

$$\dfrac{R_x}{\rho} = -\dfrac{\partial \langle \tilde{u}_x \tilde{u}_x \rangle}{\partial x} - \dfrac{\partial \langle \tilde{u}_y \tilde{u}_x \rangle}{\partial y} - \dfrac{\partial \langle \tilde{w} \tilde{u}_x \rangle}{\partial z} - \dfrac{1}{\rho} \dfrac{\partial \langle p_{\text{wave}} \rangle}{\partial x}\label{eq5.5.3.5}$$

$$\dfrac{R_y}{\rho} = -\dfrac{\partial \langle \tilde{u}_x \tilde{u}_y \rangle}{\partial x} - \dfrac{\partial \langle \tilde{u}_y \tilde{u}_y \rangle}{\partial y} - \dfrac{\partial \langle \tilde{w} \tilde{u}_y \rangle}{\partial z} - \dfrac{1}{\rho} \dfrac{\partial \langle p_{\text{wave}} \rangle}{\partial y}\label{eq5.5.3.6}$$

$$\dfrac{R_z}{\rho} = -\dfrac{\partial \langle \tilde{u}_x \tilde{w} \rangle}{\partial x} - \dfrac{\partial \langle \tilde{u}_y \tilde{w} \rangle}{\partial y} - \dfrac{\partial \langle \tilde{w} \tilde{w} \rangle}{\partial z} - \dfrac{1}{\rho} \dfrac{\partial \langle p_{\text{wave}} \rangle}{\partial z}\label{eq5.5.3.7}$$

Зверніть увагу, що$R_i$ хвильові сили не інтегровані по глибині. Дужки$\langle \ \rangle$ позначають усереднення часу за короткохвильовим періодом. Хвильовий орбітальний рух тепер позначається з ($\tilde{u}_x, \tilde{u}_y, \tilde{w}$), з тильдою, щоб відрізнити рух хвилі від середнього руху. Зверніть увагу на внесок тиску, обумовлений ненульовим усередненим за часом хвильовим тиском та термінами перенесення горизонтального імпульсу в$R_x$ і$R_y$ які безпосередньо пов'язані з радіаційними напруженнями. У$R_z$ ми визнаємо термін$-\rho \overline{\tilde{w}^2}$, який сприяв Eq. $\ref{eq5.5.3.5}$,$\ref{eq5.5.3.6}$ і$\ref{eq5.5.3.7}$. Ми також можемо розпізнати термін,$\partial \langle \tilde{u} \tilde{w} \rangle /\partial z$ який, як говорилося, діє в хвильовому прикордонному шарі, як горизонтальну силу, що штовхає потік вперед (викликаючи потоки, секта. 5.4.3).