5.5.2: Радіаційний стрес
- Page ID
- 1297
Другий закон Ньютона стверджує, що швидкість зміни імпульсу текучого елемента дорівнює силам на елемент. Хвилі можуть змінювати імпульс через чистий «приплив» або «відтік» імпульсу, або шляхом чистого припливу або відтоку імпульсу зі швидкістю частинок, або за допомогою чистої сили тиску, викликаної хвилею. Радіаційне напруження - це назва, яка була дана інтегрованому по глибині та усередненим хвилями потоку (або потоку) імпульсу за рахунок хвиль. Вперше він був визначений Лонгет-Хіггінсом і Стюартом (1964) як надлишковий потік імпульсу через наявність хвиль.
Якщо відбувається зміна хвильового імпульсного потоку (радіаційного напруження) з одного місця в інше, хвильові сили діють на рідину, впливаючи на середній рух води та рівні. Ці хвильові сили відповідають за:
- зниження середнього рівня води в мілководної зоні (установка);
- підвищення середнього рівня води в зоні прибою (настройка);
- водіння прибережної течії в разі наближення хвиль до берега (1 м/с при деяких умовах).
Визначення компонентів радіаційного напруження
Горизонтальний потік імпульсу, індукований хвилею через вертикальну площину в заданому місці, складається з:
- перенесення імпульсу\(\rho \vec{u}\) через цю площину зі швидкістю частинки, нормальною до цієї площини;
- хвильова сила тиску, що діє на площину внаслідок хвильового індукованого тиску\(p_{\text{wave}}\) у воді.
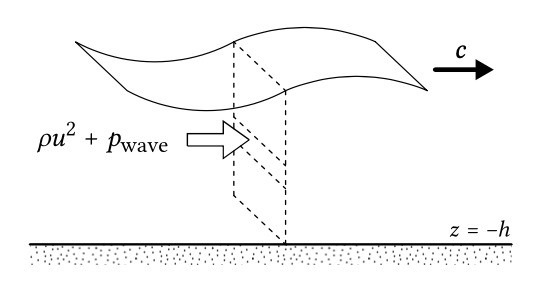
Спочатку припустимо, що розглянута площина перпендикулярна поширенню хвилі (рис.5.27). Тиск, індукований\(p_{\text{wave}}\) хвилею, діє за визначенням нормально до площини. Крім того, на кожній висоті над шаром швидкість частинок\(u\) переносить імпульс\(\rho u\) через площину (на одиницю довжини гребеня).
Малюнок 5.28: Система координат і вектор швидкості.
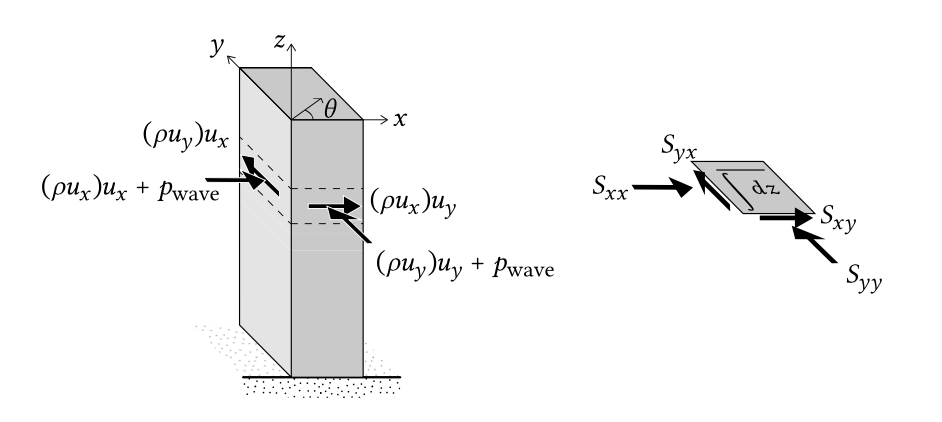
Малюнок 5.29: Схема транспортування імпульсу та компонентів радіаційного напруження в певній точці в\(x,y\) -просторі для похило падаючих хвиль. Радіаційні напруження отримані шляхом інтеграції переносу імпульсу над товщею води та усереднення за часом.
Тепер розглянемо систему координат по рис.5.28. Хвиля поширюється під кутом з\(x\) -віссю. Швидкість частинок має складову\(u_x\) в\(x\) -напрямку і складову\(u_y\) в\(y\) -напрямку. Швидкість частинок\(u_x\) транспортує як\(x\) -імпульс, так\(\rho u_x\) і\(y\) -імпульс\(\rho u_y\). Транспортування\(x\) -імпульсу швидкістю частинок\(u_x\) через вертикальну площину, перпендикулярну\(x\) осі -осі (за одиницю часу і на одиницю площі) є\((\rho u_x) u_x\) і транспорт\(y\) -імпульсу через площину є\((\rho u_y) u_x\). Імпульсні потоки можна побачити в лівій частині рис.5.29).
Рисунок 5.29 візуалізує компоненти транспортування імпульсу та радіаційного напруження в\(x\) -напрямку та\(y\) -напрямку в певній точці в\(x,y\) -просторі. Транспортування імпульсу через всю площину на одиницю довжини гребеня отримують шляхом інтеграції по глибині від дна до миттєвої поверхні води. Усереднення за часом дає загальний усереднений за хвилею перенесення\(x\) -імпульсу в\(x\) -напрямку або радіаційного напруження\(S_{xx}\):
\[S_{xx} = \underbrace{\overline{\int_{-h_0}^{\eta} (\rho u_x) u_x dz}}_{\text{part due to advection by horizontal particle velocity}} + \underbrace{\overline{\int_{-h_0}^{\eta} p_{\text{wave}} dz}}_{\text{pressure part}}\label{eq5.5.2.1}\]
\(S_{xx}\)діє нормально до розглянутої площини і тому є нормальним компонентом радіаційного напруження. Це еквівалентно нормальному напрузі, що діє в\(x\) -напрямку.
Складова радіаційного напруження\(S_{xy}\) (зсувна складова радіаційного напруження) визначається як транспорт\(x\) -імпульсу в\(y\) -напрямку. Він діє як напруга зсуву на площині (вона спрямована в\(x\) -напрямку, і працює на площині, нормальній до\(y\) -напрямку) і задається:
\[S_{xy} = \overline{\int_{-h_0}^{\eta} (\rho u_x) u_y + \tau_{xy} dz}\]
Напруга зсуву внаслідок хвиль дорівнює нулю для ірротаційної ідеальної рідини, так що ми маємо:
\[S_{xy} = \overline{\int_{-h_0}^{\eta} (\rho u_x) u_y dz} \label{eq5.5.2.3}\]
Він складається з внеску за рахунок адвекції лише горизонтальною орбітальною швидкістю. Зверніть увагу, що для особливого випадку нормально падаючих хвиль\(x\) -напрямок - це напрямок поширення хвилі,\(u_y\) а отже\(S_{xy}\), нуль.
Розглядаючи площину, нормальну до\(y\) -напрямку, ми знаходимо для імпульсних потоків в\(y\) -напрямку, нормальну складову:
\[S_{yy} = \underbrace{\overline{\int_{-h_0}^{\eta} (\rho u_y) u_y dz}}_{\text{part due to advection by horizontal particle velocity}} + \underbrace{\overline{\int_{-h_0}^{\eta} p_{\text{wave}} dz}}_{\text{pressure part}}\]
і компонент зсуву:
\[S_{yx} = \overline{\int_{-h_0}^{\eta} (\rho u_y) u_x dz} \label{eq5.5.2.5}\]
В особливому випадку, що\(x\) -direction - напрямок поширення хвилі\(u_y = 0, S_{yy}\) зменшується до частини тиску і\(S_{yx} = S_{xy} = 0\).
Вирази радіаційного напруження з використанням теорії лінійних хвиль
Використовуючи лінійну (першого порядку) хвильову теорію, можна отримати вирази для радіаційного напруження, які дійсні до другого порядку. Повне виведення можна знайти в Holthuijsen (2007). Intermezzo 5.4 дає уривок цього похідного.
Найпростіше почати з хвилі, що поширюється в позитивному\(x\) -напрямку так, щоб\(u_x = u\) і\(u_y = 0\). Якщо підставити\(u = \hat{u} \cos (\omega t - kx)\) з\(\hat{u}\) відповідно до Sect. 5.4.1 у частинці швидкісної частини еквалайзера. \(\ref{5.5.2.1}\)знаходимо (див. Holthuijsen (2007) для виведення):
\[S_{xx, \text{horizontal particle velocity}} = \overline{\int_{-h_0}^{\eta} (\rho u^2) dz} \approx \int_{-h_0}^{0} \rho \overline{u^2} dz = nE\]
де:
| \(S_{xx}, \text{hor, part, vel.}\) | радіаційне напруження в напрямку поширення хвилі внаслідок адвекції імпульсу горизонтальним орбітальним рухом | \(N/m\) |
| \(n\) | співвідношення групової швидкості і фазової швидкості | - |
| \(E\) | енергія хвилі в товщі води на\(m^2\) | \(J/m^2\) |
У випадку нерегулярних хвиль це рівняння може бути застосовано за допомогою\(E = 1/8 \rho g H_{rms}^2\). Для потоку маси ми знайшли нульовий внесок для кожного рівня нижче хвильового корита, тому що\(\bar{u} = 0\). Однак потік імпульсу є ненульовим для всієї глибини води з тих пір\(\overline{u^2} \ne 0\). Вона варіюється в принципі по глибині. Тільки на мілководді, де горизонтальна орбітальна швидкість розподілена рівномірно, частинка швидкісної частини радіаційного напруження розподіляється рівномірно.
Тиск для будь-якого рівня нижче корита дасть нульовий усереднений за часом результат відповідно до лінійної теорії. Однак існує внесок у усереднений за часом хвильовий тиск\(\overline{p_{\text{wave}}}\) через вертикальний потік імпульсу вертикальним рухом рідини. Це можна вважати вертикальним коливальним рухом рідини, що допомагає переносити вагу водяного стовпа і дається\(-\rho \overline{w^2}\), в якій\(w\) знаходиться вертикальна орбітальна швидкість. Внесок у радіаційний стрес можна знайти, замінивши лінійний вираз на середній рівень води\(w\) та інтегрувати його до нього. Знаходимо:
\[S_{xx, \text{pressure, 1}} = -\overline{\int_{-h_0}^{\bar{\eta}} \rho w^2 dz} \approx -\int_{-h_0}^{0} \rho \overline{w^2} dz = (n - 1)E\]
Крім того, є внесок у радіаційне напруження за рахунок коливань тиску між хвилевим коритом та рівнем гребеня хвилі. У секті. 5.4.2 ми припустили, що тиск між хвилевим коритом і рівнем гребеня коливається як\(\tilde{p} = \rho g \eta\). Це дає наступний чистий внесок в радіаційний стрес:
\[S_{xx, \text{pressure, 2}} = \overline{\int_{0}^{\bar{\eta}} \rho g \eta dz} = \dfrac{1}{2} \rho g \overline{\eta^2} = \dfrac{1}{2} E \label{eq5.5.2.8}\]
Це дає для напірної частини радіаційних напружень:
\[S_{xx, \text{pressure}} = \underbrace{(n - 1)E}_{\text{contribution due to (depth-varying) vertical momentum flux}} + \underbrace{1/2 E}_{\text{contribution at top of water column}} = (n - 1/2) E\label{eq5.5.2.9}\]
Термін\(\overline{w^2}\) змінюється в принципі з глибиною води, тоді як інша частина (від Eq. \(\ref{eq5.5.2.8}\)) розташовується у верхній частині водяного стовпа. На мілководді (\(n = 1\)) вертикальні орбітальні швидкості дорівнюють нулю, а напірна частина радіаційних напружень зменшується до внеску\(S_{xx, \text{pressure}} = 1/2 E\) у верхній частині товщі води. У глибокій воді\(n = 1/2\), де знаходиться компонент тиску до радіаційного напруження\((n - 1/2) E\).
Загальна напруга випромінювання в напрямку поширення хвилі (\(x\)-напрямок) тепер:
\[S_{xx} = S_{xx, \text{pressure}} + S_{xx, \text{horizontal particle velocity}} = (n -1/2) E + nE \label{eq5.5.2.10}\]
Напруги, нормальні до напрямку поширення хвилі,\(S_{yy}\) складаються\((n - 1/2) E\) лише з напірної частини. Напруги зсуву дорівнюють нулю.
З Intermezzo 5.4 - або конкретніше від Eq. \(\ref{eq5.5.2.10}\)— робимо висновок, що:
- Напірна частина радіаційного напруження дорівнює\((n - 1/2) E\). Оскільки тиск є скалярним, цей термін входить до складу радіаційних нормальних напружень у всіх напрямках.
- Величина адвективної частини радіаційного напруження, частини, обумовленої транспортом імпульсу швидкістю частинки, становить\(nE\). Це за визначенням у напрямку поширення хвилі.
За допомогою цього результату ми можемо вивести більш загальні вирази для компонентів радіаційного напруження для хвиль, що рухаються у напрямку\(\theta\) відносно\(x\) позитивного напрямку (див. Рис. Якщо\(x\) -вісь не є напрямком поширення у нас\(\vec{u} = (u_x , u_y) = (u \cos \theta, u \sin \theta)\) і з Eqs. \(\ref{eq5.5.2.1}\),\(\ref{eq5.5.2.3}\) і\(\ref{eq5.5.2.5}\) знаходимо:
\[S_{xx} = (n - \dfrac{1}{2} + n \cos^2 \theta) E \label{eq5.5.2.11}\]
\[S_{yy} = (n - \dfrac{1}{2} + n \sin^2 \theta) E\]
\[S_{xy} = S_{yx} = n \cos \theta \sin \theta E \label{eq5.5.2.13}\]
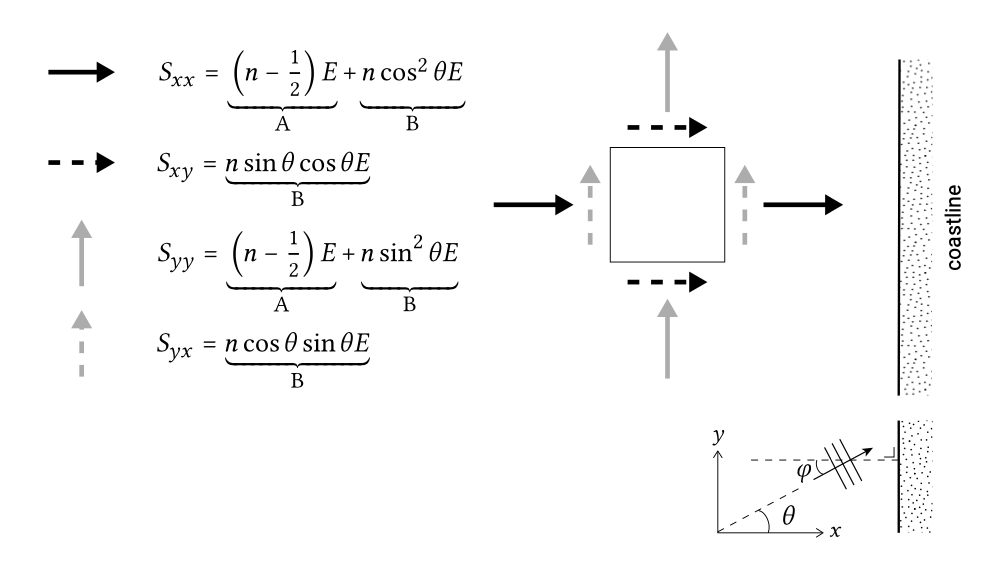
У ситуації узбережного рівномірного узбережжя позитивний\(x\) напрямок, як правило, приймається як берегово-нормальний напрямок, а позитивний\(y\) -напрямок паралельно берегової лінії. Кут падіння хвилі щодо контурів глибини тепер дорівнює куту\(\varphi\) з\(\theta\) позитивною\(x\) -віссю. Для цієї ситуації складові радіаційного напруження намальовані на рис. 5.30.
Зверніть увагу, що якщо\(x\) вісь -збігається з напрямком поширення хвилі (= 0), наведені вище Eqs. \(\ref{eq5.5.2.11}\)\(\ref{eq5.5.2.13}\)звести до:
\[S_{xx} = (2n - 1/2) E\]
\[S_{yy} = (n - 1/2) E \ \ \text{for waves propagating in the } x\text{-dircetion}\]
\[S_{xy} = S_{yx} = 0\]
Це відповідно до попередніх висновків, що:
- Нормальні напруги, перпендикулярні напрямку поширення хвилі, складаються\((n - 1/2) E\) тільки з напірної частини;
- Нормальні напруги в напрямку поширення хвилі складаються з напірної частини\((n - 1/2) E\) плюс частина за рахунок передачі імпульсу горизонтальним орбітальним рухом\(n E\);
- Напруги зсуву дорівнюють нулю, якщо\(x\) -напрямок - напрямок поширення хвилі.
У глибокій воді\(n = 1/2\), де, складовою тиску до радіаційного напруження є\((n - 1/2)E = 0\) і частина частинок рідини стає\(n E = 1/2 E\) у напрямку поширення хвилі. Таким чином, в разі поширення хвилі в\(x\) -напрямку, ми знаходимо\(S_{xx} = 1/2 E\), і\(S_{yy} = 0\). На мілководді, з іншого боку, де\(n = 1\), випливає\(S_{xx} = 3/2 E\), що, і\(S_{yy} = 1/2 E\). Тут обидва внески додають до загального радіаційного напруження\(S_{xx}\) і\(S_{yy}\) дорівнює напірної частини. Радіаційне (нормальне) напруження на мілководді явно більше, ніж у глибокій воді. І, він має дві складові на мілководді: паралельний і перпендикулярний напрямку поширення хвилі.
Радіаційне напруження при розриві хвиль
При порушенні хвиль зони серфінгу ефект поверхневого валика буде затримати вивільнення імпульсу від розриву хвилі. На практиці це означає, що рівняння для напружень випромінювання буде містити термін, обумовлений енергією ролика теж. Для цього терміну існують різні моделі, посилюючи або частину тиску, або адвекційну частину радіаційного стресу або обидва. Svendsen (1984) пропонує додатковий внесок у радіаційне напруження в напрямку поширення за рахунок швидкості в ролику на величину\(q_{\text{roller}} c = \alpha E_r\) (див. \(\ref{eq5.5.2.9}\)). Цей внесок зосереджений поблизу водної поверхні, де відбувається розрив хвилі. За припущенням мілководдя радіаційне напруження нижче рівня хвилевого корита переважає частина через адвекцію імпульсу горизонтальним орбітальним рухом (перевірте це з Intermezzo 5.4). Оскільки на мілководді горизонтальна орбітальна швидкість розподілена рівномірно, адвективна частина радіаційного напруження також розподіляється рівномірно.