5.2.2: мілководство
- Page ID
- 1242
Розглянемо лінійну (одиночну гармонійну) довгочубатий хвилю, що поширюється у воді, яка стає поступово дрібнішою (узберегове рівномірне піщане узбережжя з паралельними глибинними контурами). Хвиля нормально падає, а саме гребінь хвилі паралельний контурам глибини, рис.5.2.
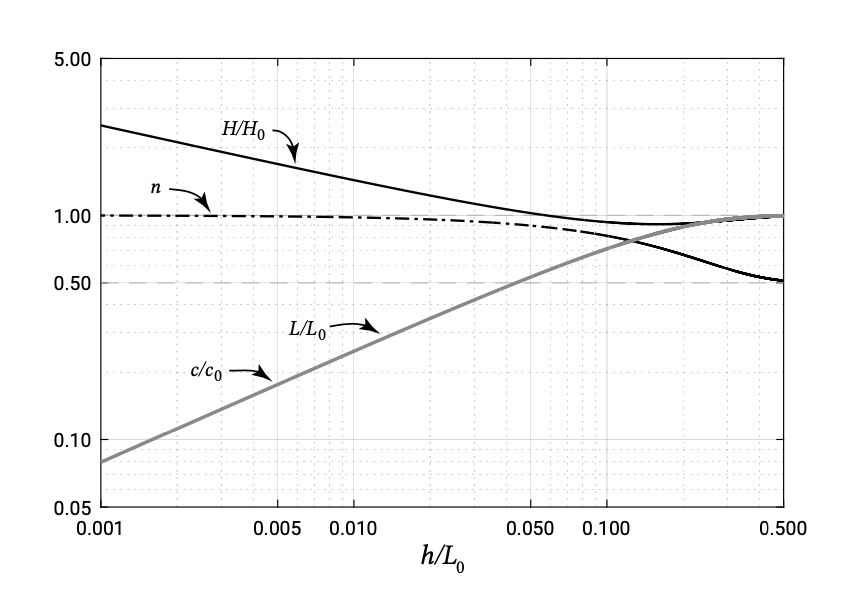
На швидкість поширення хвилі вплине дно, коли глибина води стане менше приблизно половини довжини хвилі. Зменшення глибини води дає зменшення швидкості хвилі та довжини хвилі відповідно до співвідношення дисперсії, введеного в секті. 3.5.2. На малюнку 5.3 показано\(c/c_0\) і\(L/L_0\) - де індекс 0 відноситься до умов глибокої води - як функція місцевої глибини води,\(h\) розділеної на\(L_0\). Щоб знайти зв'язок між висотою хвилі\(H\) та глибиною води,\(h\) ми повинні вивчити енергетичний баланс. Поза зоною вимикача розсіювання приблизно дорівнює нулю (нехтуючи нижнім тертям та білою кришкою) та інтеграцією еквалайзера. 5.2.1.3 врожайність:
\[U = Ec_g = Enc = \text{constant} \label{eq5.2.2.1}\]
де:
| \(U\) | потужність хвилі або потік енергії на одиницю ширини гребеня хвилі (див. Також Eq. 3.5.3.4) | \(J/(ms)\) |
| \(E\) | енергія хвилі на одиницю площі поверхні | \(J/m^2\) |
| \(cg\) | хвильова група швидкість | \(m/s\) |
| \(c\) | хвиля знаменитості | \(m/s\) |
| \(n\) | співвідношення\(c_g\) до\(c\) | - |
Еквалайзер. 3.5.3.3 і рис. 5.3 показують\(n\) залежність від глибини води і (глибокої води) довжини хвилі. Енергетичний потік ще\(U\) називають силою хвилі і являє собою швидкість, з якою енергія передається у напрямку поширення хвилі по вертикальній площині, перпендикулярній напрямку поширення хвилі і поширюється на всю глибину.
Так як\(E = 1/8 \rho g H^2\), ур. \(\ref{eq5.2.2.1}\)може використовуватися для зв'язку висот хвиль у двох довільних місцях (місця 1 і 2):
\[U_2 = U_1 \to E_2 n_2 c_2 = E_1 n_1 c_1 \to H_2^2 n_2 c_2 = H_1^2 n_1 c_1 \]
або:
\[\dfrac{H_2}{H_1} = \sqrt{\dfrac{c_1}{c_2} \dfrac{n_1}{n_2}}\]
де індекси вказують місце, в якому оцінюються параметри.
Якщо ми виберемо місце 1 у глибокій воді, де хвильові властивості легше оцінюються (\(n_1 = n_0 = 1/2\)), ми знайдемо наступне співвідношення для висоти хвилі (індекси 2 скидаються):
\[\dfrac{H}{H_0} = \sqrt{\dfrac{1}{\tanh kh} \dfrac{1}{2n}} = K_{sh}\label{eq5.2.2.4}\]
Параметр\(K_{sh}\) називається коефіцієнтом мілководіння і є чисто функцією\(kh\) (\(n\)є функцією\(kh\) тільки). На рис. 5.3 він показаний у вигляді функції\(h/L_0\). Вона становить 1,0 в глибокій воді, потім трохи зменшується з глибиною води до 0,91 і згодом піднімається до нескінченності. Насправді збільшення висоти хвилі в зоні мілководства обмежується розсіюванням через розрив хвилі. Розрив і межі розриву розглянуті трохи пізніше в цьому розділі. Відзначимо, що теорія мілководства однаково справедлива для зменшення, як і для збільшення глибини води. Це означає, що хвиля, яка проходить над місцевим мілиною, відновлює свою початкову висоту, доки не відбулося розриву.
Для того щоб визначити коефіцієнт мілководства, може бути корисним використання стандартних таблиць, що містять значення гіперболічних функцій. Ці таблиці можна знайти, наприклад, в CEM (див. Розділ. 1.7.3). Витяг з цих таблиць наведено в додатку. А.
Обміл припливів і цунамі
У цьому розділі пояснено явище мілководства для вітрових хвиль. Однак на проміжне та мілководне поширення інших хвиль, таких як цунамі та припливи, також впливають зміни глибини 1. Наприклад, в морі висоти хвиль цунамі становлять лише близько метра. Однак, коли цунамі подорожують у поступово меншу воду, їх енергія концентрується шляхом мілководства та, можливо, тунелювання 2, внаслідок чого вони крутилися і піднімаються на багато метрів у висоту.
1. Зверніть увагу, що мілководдя є відносною мірою в залежності від довжини хвилі; в секті. 3.8.1, наприклад, було продемонстровано, що океани вже є мілководдям для приливної хвилі.
2. Тунелювання - це концентрація енергії за рахунок обмеження ширини. Див. також Сект. 3.8.1 і Сект. 5.7 для прикладів.