Skip to main content
LibreTexts - Ukrayinska

5.2.4: Дифракція

  1. Last updated
  2. Save as PDF
  • Page ID
    1228

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

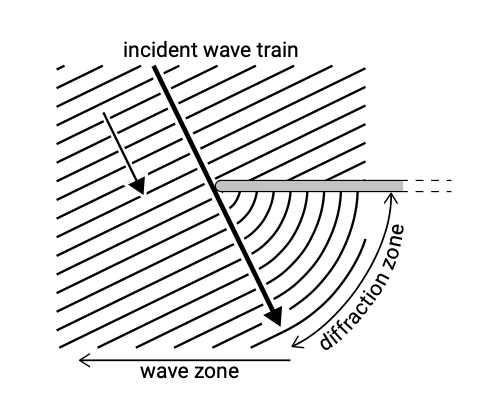
    2021-10-21 пнг
    Малюнок 5.7: Дифракція падаючого хвильового ланцюга.

    Якщо присутні перешкоди поширенню хвиль (офшорний острів, хвилеріз, мис) або різкі зміни нижніх контурів, спостерігається велика (початкова) зміна енергії хвилі вздовж гребеня хвилі, що призводить до передачі енергії вздовж гребенів хвиль. Це явище називається дифракцією. На малюнку 5.7 показана дифракція падаючого хвильового ланцюга в тому випадку, якщо зміни глибини відсутні. Частина хвильового фронту перекрита хвилерізом і відбивається в сторону моря. Залишок хвильового фронту буде прогинатися навколо перешкоди і таким чином проникати в зону в леді перешкоди (тіньова зона). Дифракційні гребені хвилі утворюватимуть концентричні кругові дуги з висотою хвилі, що зменшується вздовж гребеня кожної хвилі.

    На малюнку 5.7 також показаний хвильовий промінь, який відокремлює тіньову або дифракційну зону від хвильової зони. Завдяки бічній передачі енергії хвилі в тіньову зону висота хвилі вздовж цього променя нижча за висоту падаючої хвилі; у випадку постійної глибини (і, отже, постійної швидкості) висота хвилі становить 50% від початкової висоти хвилі відповідно до лінійної теорії та порядку 70% для нерегулярного напрямку хвилі. Висота хвиль зменшується глибше в тіньову зону. Далі від хвилерізу в хвильову зону висота хвилі поступово наближається до висоти падаючої хвилі.

    Ступінь проникнення енергії в область на землю перешкоди залежить від співвідношення характерної бічної розмірності перешкоди, наприклад, довжини одного відокремленого хвилерізу\(\lambda\) до довжини хвилі\(L\). Коли тонка купа стоїть хвилями з великою довжиною хвилі\(\lambda /L \ll 1\), хвильова енергія поширюється позаду всієї палі. У разі довгого відокремленого хвилерізу\(\lambda /L \gg 1\), дифракція відбувається навколо кожного головки хвилерізу, але енергія хвилі не буде поширюватися по всій зоні за хвилерізом.

    2021-10-21 пнг
    Малюнок 5.8: Типова дифракційна картина через зазор між двома окремими хвилерізами в Пезаро, Італія. Фото Роберто Ло Савіо («Кредити» на сторінці 575).

    На малюнку 5.8 показані хвилі, що проходять через зазор між двома відокремленими хвилерізами. Дифракція відбувається в леді хвилерізів по обидва боки щілини. Для досить великих довжин зазорів (щодо довжини хвилі) ці дифракційні моделі є незалежними. Взаємодія двох моделей може відбуватися при меншій довжині зазору.

    Теорія дифракції хвиль вирішується математично шляхом застосування «Корнуспірального» (див., наприклад, Battjes (2006)). Цей графічний метод дає просторово змінні коефіцієнти дифракції, визначені як відношення висоти дифракційної хвилі до висоти падаючої хвилі, припускаючи, що остання не порушена перешкодою. Глава II-7 CEM і (більш детально) Керівництво по захисту берега Том I Глава 2 представляють коефіцієнти дифракції як функція положення (щодо напівнескінченного жорсткого непроникного хвилерізу) і як функція ширини щілини хвилеріз.

    Недоліком перерахованих вище способів є те, що вони припускають постійну глибину води. Насправді, як правило, буде похиле дно або нерівне ліжко, і тому на результати впливатиме це дно. Числові моделі можуть враховувати мілководство, дифракцію, заломлення, відображення (і розрив) одночасно.