3.7.6: Приливні складові

Основні приливні складові наведені в таблиці 3.5. Ми бачили в секті. 3.7.3 що основний місячний приплив має період 12.42 год, а основний сонячний приплив - період 12 год відповідно. Ці приливні складові (або приливні компоненти) називаються\(M2\) і\(S2\). Вплив сонця характеризується буквою\(S\), впливом Місяця буквою\(M\). Індекс 2 відноситься до явищ, які відбуваються двічі на день. Амплітуди та фази цих двох складових змінюються залежно від місця розташування на землі.

Таблиця 3.5: Основні приливні складові з рівноважними амплітудами від Apel (1987)

Приливні складові	Ім'я	Амплітуда рівноваги [м]	Період [h]
Напівдобовий
Основний місячний	М2	0,24	12.42
Основні сонячні	S2	0,11	12.00
Місячний еліптичний	N2	0.046	12.66
Місячно-сонячне відхилення	К2	0.031	11.97
добовий
Місячно-сонячне відхилення	К1	0,14	23.93
Основний місячний	O1	0,10	25.82
Основні сонячні	Р1	0.047	24.07
Місячний еліптичний	Q1	0,019	26.87
Тривалий період
Двотижнево	Мф	0.042	327,9
Щомісячно	Мм	0,022	661.3
Піврічні	Море	0,019	4383

Приливні варіації в порядку дециметрів тільки у відкритих океанах. Відповідно до теорії рівноваги амплітуди\(M2\) і\(S2\) складають 0,24 м і 0,11 м відповідно. Це дає коефіцієнт\(S2/M2\) = 0,46, який також можна обчислити за допомогою Eqs. 3.7.3.1 і 3.7.3.2 як\(S2/M2\) = 0,515/1,13 = 0,46. \(S2\)Сигнали\(M2\) та мають дещо іншу частоту, що призводить до так званого биття двох сигналів, що призводить до мінливості припливу весни: коли\(S2\) компоненти\(M2\) та знаходяться у фазі (Місяць і сонце вирівняні), це весняний приплив, а коли вони виходять з фаза - це приплив припливу. Це ми бачили раніше в секті. 3.7.4. Биття двох сигналів, що призводить до зміни амплітуд протягом місячного місяця, порівнянне з биттям двох хвильових поїздів з дещо різними частотами, що призводить до зміни амплітуди або модуляції за шкалою хвильової групи, як це розглядається в Секті. 3.5.3. Intermezzo 3.4 розглядає цю амплітудну модуляцію більш детально.

Інтермеццо 3.4 Астрономічні складові

Малюнок 3.25: Взаємодія між\(M2\) і\(S2\) призводить до зміни весни та припливу. Переконайтеся, що період биття\(M2\) і\(S2\) становить 14,7 днів (див. груповий період для вітрових хвиль Eq. 3.5.3.2).

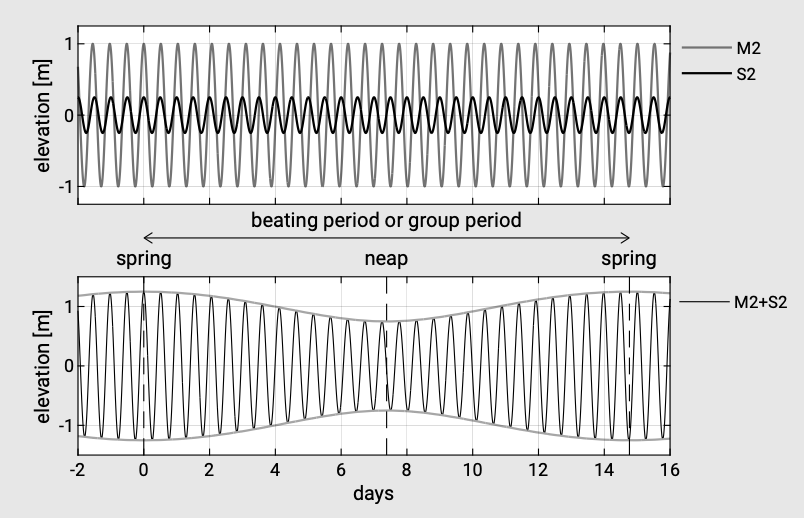
Розділ 3.7.6 описав океанський приплив як синусоїдальну напівдобову варіацію рівня води, модифіковану двотижневою варіацією весни та припливу та з добовою нерівністю. Варіація припливу пружини та припливу є результатом лінійного підсумовування головних компонентів з невеликою диференціальною частотою. Розглянемо\(M2\) і\(S2\) складові. Лінійна комбінація цих двох приливних складових з невеликою різницею в частоті призводить до зміни амплітуди з періодом, який визначається\(\omega_{S2} - \omega_{M2}\), порівнянним з биттям двох короткохвильових поїздів з дещо різними частотами (див. 3.5.3). Це показано на рис.3.25.

Малюнок 3.26: Взаємодія між\(M2\) і\(K1\) призводить до добової нерівності між двома послідовними високими водами та між двома послідовними низькими водами. Також може спостерігатися більш повільне зміна амплітуди.

Добова нерівність для переважно напівдобового припливу є результатом підсумовування напівдобової і добової складових і продемонстровано на рис. 3.26 для\(M2\) і\(K1\). Результатом є послідовність двох симетричних припливів з різним діапазоном припливів (різниця між висотами двох послідовних висот називається добовою нерівністю).

Схилення земної осі вносить напівдобові і добові приливні складові\(K1\),\(K2\)\(O1\) і\(P1\). Добові компоненти несуть індекс 1. \(K1\)з\(O1\) виражає ефект схилення Місяця,\(K1\)\(P1\) з схилянням сонця. \(K1\),\(P1\) і\(O1\) враховують добову нерівність (див. Інтермеццо 3.4) і, в крайності, добові припливи (де напівдобова складова повністю зникла). \(K2\)Складова модулює амплітуду\(M2\) і частоту і\(S2\) для схильного впливу Місяця і сонця відповідно. Інші ефекти породжуватимуть інші приливні складові, визначені точним періодом, зі своїми амплітудами відповідно до теорії рівноваги та з власними фазами відносно один одного. Наприклад, відстань Місяця від Землі змінюється, оскільки орбіта Місяця є еліптичною і тому, що еліптична орбіта не фіксована. Цей ефект вводить напівдобові і добові складові\(N2\) і\(Q1\). Найдовший період - 18,6 років, що є періодом зміни місячного схилення на 5°.

Для практичних цілей приплив можна розглядати як синусоїдальну напівдобову зміну рівня води, модифіковану двотижневою зміною амплітуди весни та припливу та з добовою нерівністю, яка змінюється залежно від широти та щомісячного та річного циклу. В крайньому випадку добова нерівність настільки велика, що зміна рівня води є виключно добовим.

Малюнок 3.27: Спектр рівноважних припливів з частотами близько двох разів на добу. Верхній: спектр розділений на групи, розділені циклом на місяць (0,55 °/год). Нижня: розширений спектр\(S2\) групи, показуючи розщеплення при циклі на рік (0,04 °/год). Найтонше розщеплення в цьому показнику відбувається при циклі за 8,847 років (0,0046 °/год). (Від Річарда Інеса, Центр космічних досліджень Техаського університету в Стюарті, 2008, див. Також https://github.com/introocean/introocean-en).

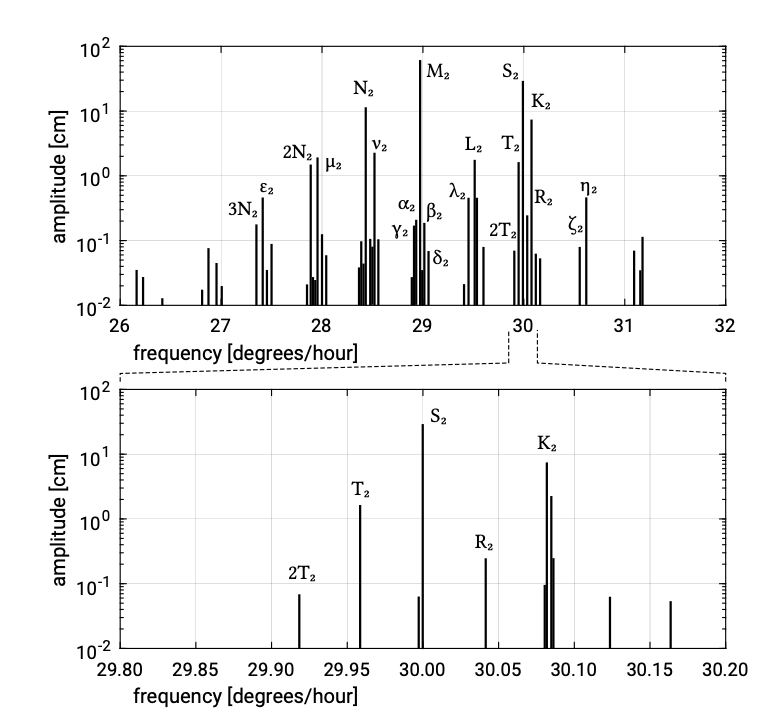
\(M2\)і\(S2\) є основними, але не єдиними складовими з частотами близько двох разів на добу (див. Рис. Відзначимо, що спектр рівноважних припливів на рис. 3.27 складається з дискретних ліній; припливи мають точні частоти, що визначаються орбітами землі і Місяця, і їх спектр не є безперервним. Ми бачили раніше, що океанські хвилі мають всі можливі частоти, а їх спектр безперервний.