Skip to main content
LibreTexts - Ukrayinska

3.7.3: Диференціальна тяга або сила, що генерує прилив

  1. Last updated
  2. Save as PDF
  • Page ID
    1613

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Рівняння 3.7.2.1 і 3.7.2.2 показують, що гравітаційна тяга Сонця на два порядки більше гравітаційної тяги Місяця. Цього ми могли очікувати, оскільки земля обертається навколо Сонця, а не Місяця. Проте сонце сприяє лише близько 30% припливних амплітуд в океанах, а Місяць відповідає за решту 70%. Причина полягає в тому, що не гравітаційна тяга сама по собі відповідає за сили, що генерують приливи.

    У вищесказаному ми бачили, що гравітаційне тяжіння забезпечує доцентрове прискорення, яке підтримує рух землі навколо центру ваги системи земля-сонце (земля-місяць). З гравітаційним тяжіння для землі в цілому (Eqs. 3.7.2.1 і 3.7.2.2) припадає 4, приплив породжується набагато більш тонким ефектом, тобто різницею між гравітаційною тягою на водні маси океану, які розташовані на різній відстані від Сонця і Місяця.

    Розглянемо 1 кг маси на ближній стороні землі, яка, отже, є радіусом землі\(R = 6.37 \times 10^6\) m ближче до Сонця, ніж центр землі. Гравітаційна тяга Сонця на 1 кг маси на ближньому боці землі\(\Delta a_s\) більше\(a_s\), ніж, тобто:

    \[\begin{array} {c} {\Delta a_s = a_{s, near\ side} -a_s = G \dfrac{M_s}{(d_s - R)^2} - G \dfrac{M_s}{d_s^2} \approx} \\ {2G \dfrac{M_s R}{d_s^3} = a_s \dfrac{2R}{d_s} = 0.515 \times 10^{-7} g} \end{array}\]

    Це відоме як диференціальна тяга. Зверніть увагу, що\(a_s\) це перший порядок обернено пропорційний кубу відстані. Аналогічно для Місяця:

    \[\Delta a_m \approx 2G \dfrac{M_m R}{d_m^3} = a_m \dfrac{2R}{d_m} = 1.13 \times 10^{-7} g\]

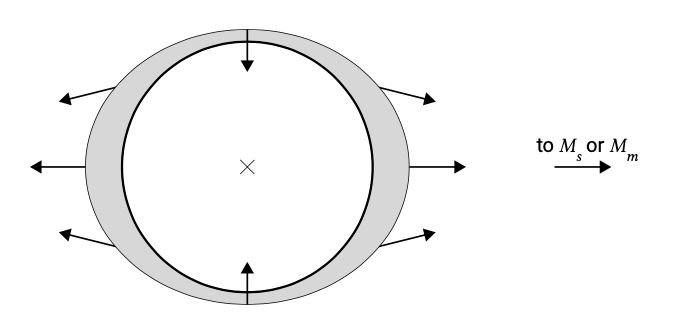
    2021-10-14 пнг
    Малюнок 3.18: Напрямок і відносні величини диференціальної гравітаційної тяги в різних місцях земної поверхні. У кожному місці він задається векторним відніманням\(a_{s \ or \ m, local}\) і частиною\(a_{s \ or \ m}\), яка забезпечує доцентрове прискорення. Зображені приливні опуклості виходять з тангенціальних складових диференціальної тяги (див. Рис.

    Точка, найвіддаленіша від сонця (місяця), в свою чергу, менша, ніж\(a_s (a_m)\) на ту саму величину,\(\Delta a_s (\Delta a_m)\) яку можна показати аналогічним розрахунком. Проведення розрахунку для всіх місць на землі призводить до диференціальної тяги на землі, як зазначено схематично на рис.3.18 (порівняти з рис.3.17).

    Диференціальна тяга відповідає за приливну генерацію і тому також називається приливною силою. Оскільки\(\Delta a\) пропорційна сонячному\(M/d^3\) диференціальному тягу\(\Delta a_s\) лише в 0,46 рази перевищує місячний диференціальний тяга\(\Delta a_m\). Місяць відповідає за 69% припливного механізму як\(\Delta a_m /(\Delta a_m + \Delta a_s)\) = 69%.

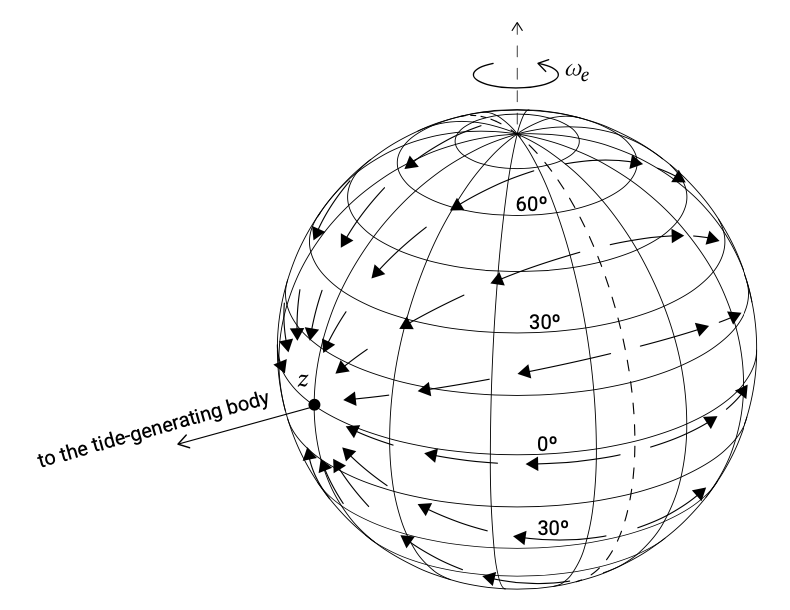
    2021-10-14 пнг
    Малюнок 3.19: Горизонтальна складова приливної сили на землі, коли приливообразующее тіло (земля або місяць) знаходиться вище екватора в\(z\).

    Диференціальна тяга, намальована на рис. 3.18, має складові нормальні і паралельні земній поверхні. Нормальні компоненти на багато порядків менше, ніж власне гравітаційне тяжіння землі. Наприклад, для точки, найближчої до Сонця, диференціальне прискорення є нормальним до земної поверхні і з\(0.515 \times 10^{-7} g\) його величиною незначне порівняно з\(g\). Тангенціальні або «горизонтальні» компоненти мають той самий порядок величини, що і нормальні компоненти, але оскільки вони перпендикулярні полю земної сили тяжіння, ними не можна нехтувати. Дотичні сили продемонстровані на рис.3.19.

    Вплив дотичних сил полягає в зміщенні води в сторону землі, звернену до Сонця (Місяць), і в протилежну сторону в приливних опуклостей (див. Рис. 3.18). Нагромадження води за рахунок дотичних сил врівноважується градієнтами тиску в протилежному напрямку за рахунок похилої водної поверхні. Якби земля була повністю покрита водою, її рівноважна конфігурація була б еліпсоїдом (м'яч для регбі або яйце).

    Швидке добове обертання землі навколо власної осі змушує землю обертатися під приливними опуклості, створюючи тим самим напівдобовий приплив з двома високими та двома низькими водами, що проходять одну і ту ж точку на землі щодня. Період сонячного припливу дорівнює рівно 12 ч (наш день вимірюється в плані сонця, Intermezzo 3.3). Період місячного припливу регулюється періодом між місячними фазами або місячним днем. Період напівдобового місячного припливу при цьому дорівнює половині місячного дня = 12 годин 25 хвилин.

    Intermezzo 3.3: Рухи землі, земля-місяць і земля-сонце системи

    Земля кружляє сонце за 365,25 днів. Земля обертається навколо власної осі за 23 години 56 хвилин (сидеричний день, щодо зірок) в тому ж напрямку, в якому Місяць обертається навколо землі і землі навколо Сонця. У той час як земля завершує одне щоденне обертання, земля також обертається відносно сонця. Як результат, лише через 24 години або один (сонячний) день земля повертається в тому ж положенні щодо сонця, яке бачить спостерігач на землі. Місячний день триває ще довше, а саме 24 години 50 хвилин. Це відбувається тому, що Місяць прогресує по своїй орбіті навколо Землі під час щоденного обертання Землі. Додаткові 50 хвилин потрібні для того, щоб земля «наздогнала» Місяць, як буде пояснено нижче.

    Період обертання Місяця навколо землі становить 27,3 дня (сидеричний місяць). Місяць займає 29,5 днів, щоб повернутися в те ж положення щодо сонця, яке бачить спостерігач на землі. Такий місячний місяць - це час між послідовними повтореннями однієї і тієї ж фази; наприклад, між повним місяцем і повним місяцем. Протягом 27,3 днів сидеричного місяця земля рухалася по своїй орбіті навколо Сонця, і тепер Місяць повинен «наздогнати» до цього нового положення. Це займає 2,2 дня, щоб зробити це.

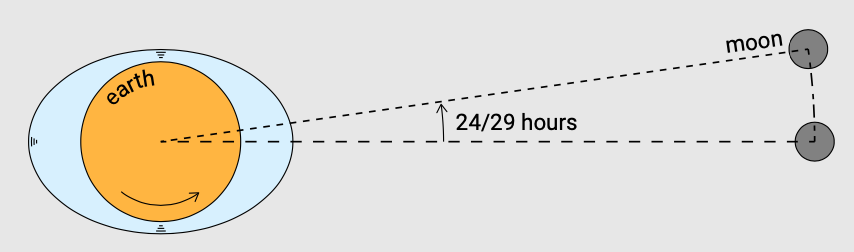
    2021-10-14 пнг
    Малюнок 3.20: Місячний день (час між послідовними транзитами Місяця для спостерігача на землі) становить 24 години 50 хвилин.

    Далі, поки Місяць прогресує по своїй орбіті навколо Землі, земля обертається навколо власної осі. Земля повинна обертатися трохи більше, ніж повне обертання, перш ніж будь-яке задане місце «наздожене» місячну опуклість. Під час одного обертання Землі навколо своєї осі Місяць покрила 1/29,5 частини своєї загальної орбіти навколо Землі (по відношенню до Сонця). Тому місячний день дорівнює\((1 + 1/29.5) \times 24\) h = 24 ч 50 хв. На малюнку 3.20 показано необхідне додаткове обертання землі, щоб наздогнати Місяць.

    4. Альтернативні, але еквівалентні пояснення (див. Конспекти лекцій DUT CTB2410 та CIE5317) приймають рухому землю як опорну рамку та вводять «фіктивні» відцентрові сили (див. Також Intermezzo 3.1). Завдяки обертанню землі навколо центру ваги системи земля-сонце (земля-місяць) виникає спрямована назовні відцентрова сила, однакова в кожній точці землі і спрямована паралельно лінії центрів. Відцентрове прискорення (сила на одиницю маси) врівноважує гравітаційне прискорення земного центру до Сонця (Місяця).