14.7: Проблеми максимума/мінімуму
- Page ID
- 61842
- Використовуйте часткові похідні, щоб знайти критичні точки для функції двох змінних.
- Застосуйте другий тест похідної для ідентифікації критичної точки як локального максимуму, локального мінімуму або точки сідла для функції двох змінних.
- Вивчіть критичні точки та граничні точки, щоб знайти абсолютні максимальні та мінімальні значення для функції двох змінних.
Одним з найбільш корисних додатків для похідних функції однієї змінної є визначення максимальних і/або мінімальних значень. Ця програма також важлива для функцій двох або більше змінних, але, як ми бачили в попередніх розділах цієї глави, введення більш незалежних змінних призводить до більш можливих результатів для обчислень. Основні ідеї пошуку критичних точок і використання похідних тестів все ще дійсні, але при оцінці результатів з'являються нові зморшки.
Критичні точки
Для функцій однієї змінної визначено критичні точки як значення змінної, при якій похідна функції дорівнює нулю або не існує. Для функцій двох і більше змінних поняття по суті однакове, за винятком того, що ми зараз працюємо з частковими похідними.
\(z=f(x,y)\)Дозволяти бути функція двох змінних, яка диференціюється на відкритому множині, що містить точку\((x_0,y_0)\). Точка\((x_0,y_0)\) називається критичною точкою функції двох змінних,\(f\) якщо виконується одна з двох наступних умов:
- \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\)
- Або\(f_x(x_0,y_0) \; \text{or} \; f_y(x_0,y_0)\) не існує.
Знайдіть критичні точки кожної з наступних функцій:
- \(f(x,y)=\sqrt{4y^2−9x^2+24y+36x+36}\)
- \(g(x,y)=x^2+2xy−4y^2+4x−6y+4\)
Рішення
а. Для початку розраховуємо\(f_x(x,y) \; \text{and} \; f_y(x,y):\)
\[\begin{align*} f_x(x,y) &=\dfrac{1}{2}(−18x+36)(4y^2−9x^2+24y+36x+36)^{−1/2} \\[4pt] &=\dfrac{−9x+18}{\sqrt{4y^2−9x^2+24y+36x+36}} \end{align*}\]
\[\begin{align*} f_y(x,y) &=\dfrac{1}{2}(8y+24)(4y^2−9x^2+24y+36x+36)^{−1/2} \\[4pt] &=\dfrac{4y+12}{\sqrt{4y^2−9x^2+24y+36x+36}} \end{align*}. \nonumber \]
Далі ставимо кожне з цих виразів рівним нулю:
\[\begin{align*} \dfrac{−9x+18}{\sqrt{4y^2−9x^2+24y+36x+36}} &=0 \\[4pt] \dfrac{4y+12}{\sqrt{4y^2−9x^2+24y+36x+36}} &=0. \end{align*}\]
Потім помножте кожне рівняння на загальний знаменник:
\[\begin{align*} −9x+18 &=0 \\[4pt] 4y+12 &=0. \end{align*}\]
Тому\(x=2\) і\(y=−3,\) так\((2,−3)\) є критичною точкою\(f\).
Ми також повинні перевірити можливість того, що знаменник кожної часткової похідної може дорівнювати нулю, що призводить до того, що часткова похідна не існує. Оскільки знаменник однаковий у кожній частковій похідній, нам потрібно зробити це лише один раз:
\[4y^2−9x^2+24y+36x+36=0. \label{critical1} \]
Рівняння\ ref {critical1} являє собою гіперболу. Слід також зазначити, що область\(f\) складається з точок, що задовольняють нерівності.
\[4y^2−9x^2+24y+36x+36≥0. \nonumber \]
Тому будь-які точки на гіперболі - це не тільки критичні точки, вони також знаходяться на кордоні домену. Щоб поставити гіперболу в стандартному вигляді, скористаємося методом заповнення квадрата:
\[\begin{align*} 4y^2−9x^2+24y+36x+36 &=0 \\[4pt] 4y^2−9x^2+24y+36x &=−36 \\[4pt] 4y^2+24y−9x^2+36x &=−36 \\[4pt] 4(y^2+6y)−9(x^2−4x) &=−36 \\[4pt] 4(y^2+6y+9)−9(x^2−4x+4) &=−36−36+36 \\[4pt] 4(y+3)^2−9(x−2)^2 &=−36.\end{align*}\]
Поділ обох сторін на\(−36\) ставить рівняння в стандартному вигляді:
\[\begin{align*} \dfrac{4(y+3)^2}{−36}−\dfrac{9(x−2)^2}{−36} &=1 \\[4pt] \dfrac{(x−2)^2}{4}−\dfrac{(y+3)^2}{9} &=1. \end{align*}\]
Зверніть увагу,\((2,−3)\) що точка є центром гіперболи.
Таким чином, критичними точками функції\(f\) є\( (2, -3) \) і всі точки на гіперболі,\(\dfrac{(x−2)^2}{4}−\dfrac{(y+3)^2}{9}=1\).
б. Для початку розрахуємо\(g_x(x,y)\) і\(g_y(x,y)\):
\[\begin{align*} g_x(x,y) &=2x+2y+4 \\[4pt] g_y(x,y) &=2x−8y−6. \end{align*}\]
Далі ставимо кожне з цих виразів рівним нулю, що дає систему рівнянь в\(x\) і\(y\):
\[\begin{align*} 2x+2y+4 &=0 \\[4pt] 2x−8y−6 &=0. \end{align*}\]
Віднімання другого рівняння з першого дає\(10y+10=0\), так\(y=−1\). Підставляючи це в перше рівняння дає\(2x+2(−1)+4=0\), так\(x=−1\).
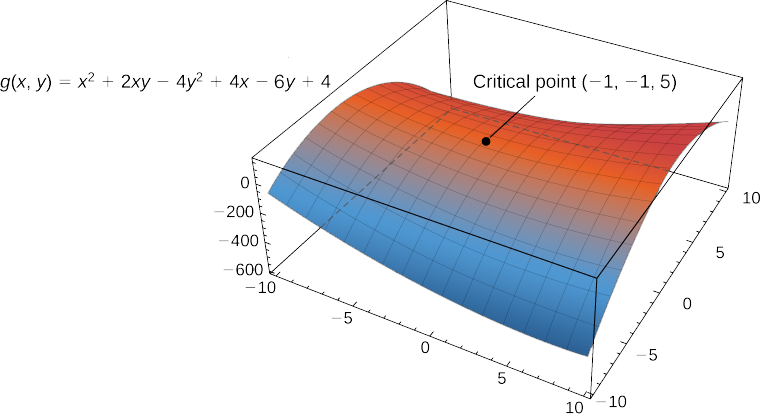
Тому\((−1,−1)\) є критичною точкою\(g\). Немає жодних моментів\(\mathbb{R}^2\), які роблять або часткову похідну не існує.
\(\PageIndex{1}\)На малюнку показано поведінку поверхні в критичній точці.
Знайти критичну точку функції\(f(x,y)=x^3+2xy−2x−4y.\)
- Підказка
-
Обчисліть\(f_x(x,y)\) і\(f_y(x,y)\), після чого встановіть їх рівним нулю.
- Відповідь
-
Єдина критична точка\(f\) - це\((2,−5)\).
Основною метою визначення критичних точок є розташування відносних максимумів і мінімумів, як при однозмінному численні. При роботі з функцією однієї змінної визначення локального екстремуму передбачає знаходження інтервалу навколо критичної точки таким чином, щоб значення функції було або більше, або менше всіх інших значень функції в цьому інтервалі. При роботі з функцією двох і більше змінних працюємо з відкритим диском навколо точки.
\(z=f(x,y)\)Дозволяти функція двох змінних, яка визначається і безперервно на відкритому множині, що містить точку\((x_0,y_0).\) Тоді\(f\) має локальний максимум в\((x_0,y_0)\) якщо
\[f(x_0,y_0)≥f(x,y) \nonumber \]
для всіх точок\((x,y)\) в межах деякого диска з центром\((x_0,y_0)\). Число\(f(x_0,y_0)\) називається локальним максимальним значенням. Якщо попередня нерівність тримається для кожної точки\((x,y)\) в області\(f\), то\(f\) має глобальний максимум (також званий абсолютним максимумом) при\((x_0,y_0).\)
Функція\(f\) має локальний мінімум при\((x_0,y_0)\) if
\[f(x_0,y_0)≤f(x,y) \nonumber \]
для всіх точок\((x,y)\) в межах деякого диска з центром\((x_0,y_0)\). Число\(f(x_0,y_0)\) називається локальним мінімальним значенням. Якщо попередня нерівність тримається для кожної точки\((x,y)\) в області\(f\), то\(f\) має глобальний мінімум (також називається абсолютним мінімумом) при\((x_0,y_0)\).
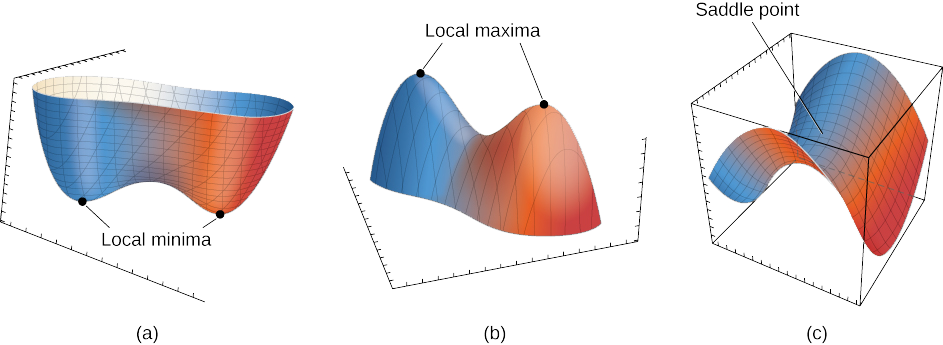
Якщо\(f(x_0,y_0)\) це або локальне максимальне, або локальне мінімальне значення, то воно називається локальним екстремумом (див. Наступний малюнок).

У Обчисленні 1 показано, що екстремуми функцій однієї змінної виникають у критичних точках. Те ж саме справедливо і для функцій більш ніж однієї змінної, як зазначено в наступній теоремі.
\(z=f(x,y)\)Дозволяти бути функція двох змінних, яка визначена і безперервна на відкритому множині, що містить точку\((x_0,y_0)\). Припустимо,\(f_x\) і\(f_y\) кожен існує на\((x_0,y_0)\). Якщо f має локальний екстремум в\((x_0,y_0)\), то\((x_0,y_0)\) є критичною точкою\(f\).
Другий похідний тест
Розглянемо функцію\(f(x)=x^3.\) Ця функція має критичну точку в\(x=0\), так як\(f'(0)=3(0)^2=0\). Однак\(f\) не має екстремального значення при\(x=0\). Тому існування критичного значення при\(x=x_0\) не гарантує локального екстремуму при\(x=x_0\). Те ж саме справедливо і для функції двох або більше змінних. Один із способів це може статися - це точка сідла. Приклад точки сідла відображається на наступному малюнку.
Малюнок\(\PageIndex{3}\): Графік функції\(z=x^2−y^2\). Цей графік має сідлову точку на початку.
На цьому графіку початком є точка сідла. Це пов'язано з тим, що перші часткові\((x,y)=x^2−y^2\) похідні f обидва рівні нулю в цій точці, але це не є ні максимумом, ні мінімумом для функції. Крім того, вертикальний слід, відповідний\(y=0\) є\(z=x^2\) (парабола, що відкривається вгору), але вертикальний слід, відповідний\(x=0\) є\(z=−y^2\) (парабола, що відкривається вниз). Тому це як глобальний максимум для одного сліду, так і глобальний мінімум для іншого.
З огляду\(z=f(x,y),\) на функцію, точка\(\big(x_0,y_0,f(x_0,y_0)\big)\) є точкою сідла, якщо обидва\(f_x(x_0,y_0)=0\) і\(f_y(x_0,y_0)=0\), але\(f\) не має локального екстремуму при\((x_0,y_0).\)
Другий тест похідної для функції однієї змінної надає метод визначення того, чи виникає екстремум у критичній точці функції. При розширенні цього результату на функцію двох змінних виникає питання, пов'язане з тим, що насправді існує чотири різні часткові похідні другого порядку, хоча рівність змішаних часткових зводить це до трьох. Другий тест похідної для функції двох змінних, викладеного в наступній теоремі, використовує дискримінант,\(D\) який замінює\(f''(x_0)\) у другому тесті похідної функцію однієї змінної.
\(z=f(x,y)\)Дозволяти функція двох змінних, для яких часткові похідні першого та другого порядку є неперервними на деякому диску, що містить точку\((x_0,y_0)\). Припустимо\(f_x(x_0,y_0)=0\) і\(f_y(x_0,y_0)=0.\) визначимо кількість
\[D=f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)−\big(f_{xy}(x_0,y_0)\big)^2. \nonumber \]
Потім:
- Якщо\(D>0\) і\(f_{xx}(x_0,y_0)>0\), то f має локальний мінімум при\((x_0,y_0)\).
- Якщо\(D>0\) і\(f_{xx}(x_0,y_0)<0\), то f має локальний максимум at\((x_0,y_0)\).
- Якщо\(D<0\), то\(f\) має сідлову точку в\((x_0,y_0)\).
- Якщо\(D=0\), то тест непереконливий.
Див\(\PageIndex{4}\). Малюнок.
Щоб застосувати другий тест похідної, необхідно, щоб ми спочатку знайшли критичні точки функції. У всій процедурі задіяно кілька етапів, які окреслені в стратегії вирішення проблем.
\(z=f(x,y)\)Дозволяти функція двох змінних, для яких часткові похідні першого та другого порядку є неперервними на якомусь диску, що містить точку\((x_0,y_0).\) Щоб застосувати другий тест похідної для пошуку локальних екстремумів, скористайтеся наступними кроками:
- Визначте критичні\((x_0,y_0)\) точки функції,\(f\) де\(f_x(x_0,y_0)=f_y(x_0,y_0)=0.\) Відкиньте будь-які точки, де хоча б одна з часткових похідних не існує.
- Обчисліть дискримінант\(D=f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)−\big(f_{xy}(x_0,y_0)\big)^2\) для кожної критичної точки\(f\).
- Застосуйте чотири випадки тесту, щоб визначити, чи є кожна критична точка локальним максимумом, локальним мінімумом або точкою сідла, чи теорема є непереконливою.
Знайдіть критичні точки для кожної з наступних функцій і використовуйте другий тест похідної, щоб знайти локальну крайність:
- \(f(x,y)=4x^2+9y^2+8x−36y+24\)
- \(g(x,y)=\dfrac{1}{3}x^3+y^2+2xy−6x−3y+4\)
Рішення
а. крок 1 стратегії вирішення проблем передбачає знаходження критичних точок\(f\). Для цього спочатку обчислюємо\(f_x(x,y)\) і\(f_y(x,y)\), потім встановлюємо кожен з них рівним нулю:
\[\begin{align*} f_x(x,y) &=8x+8 \\[4pt] f_y(x,y) &=18y−36. \end{align*}\]
Встановлення їх рівних нулю дає систему рівнянь.
\[\begin{align*} 8x+8 &=0 \\[4pt] 18y−36 &=0. \end{align*}\]
Рішенням цієї системи є\(x=−1\) і\(y=2\). Тому\((−1,2)\) є критичною точкою\(f\).
Крок 2 стратегії вирішення проблем передбачає обчислення.\(D.\) Для цього спочатку обчислюємо другі часткові похідні\(f:\)
\[\begin{align*} f_{xx}(x,y) &=8 \\[4pt] f_{xy}(x,y) &=0 \\[4pt] f_{yy}(x,y) &=18. \end{align*}\]
Тому,\(D=f_{xx}(−1,2)f_{yy}(−1,2)−\big(f_{xy}(−1,2)\big)^2=(8)(18)−(0)^2=144.\)
Крок 3 передбачає застосування чотирьох випадків тесту для класифікації поведінки функції в цій критичній точці.
Так як\(D>0\) і\(f_{xx}(−1,2)>0,\) це відповідає випадку 1. Тому\(f\) має локальний мінімум на,\((−1,2)\) як показано на наступному малюнку.
Малюнок\(\PageIndex{5}\): Функція\(f(x,y)\) має локальний мінімум на\((−1,2,−16).\) Примітка. Масштаб на\(y\) осі -у цьому графіку обчислюється тисячами.
б. для кроку 1 спочатку обчислюємо\(g_x(x,y)\) і\(g_y(x,y)\), потім встановлюємо кожен з них рівним нулю:
\[\begin{align*} g_x(x,y) &=x^2+2y−6 \\[4pt] g_y(x,y) &=2y+2x−3. \end{align*}\]
Встановлення їх рівних нулю дає систему рівнянь.
\[\begin{align*} x^2+2y−6 &=0 \\[4pt] 2y+2x−3 &=0. \end{align*}\]
Для вирішення цієї системи спочатку вирішують друге рівняння для\(y\). Це дає\(y=\dfrac{3−2x}{2}\). Підставляючи це в перше рівняння, дає
\[\begin{align*} x^2+3−2x−6 &=0 \\[4pt] x^2−2x−3 &=0 \\[4pt] (x−3)(x+1) &=0. \end{align*}\]
Тому\(x=−1\) або\(x=3\). Підстановка цих значень у рівняння\(y=\dfrac{3−2x}{2}\) дає критичні точки\(\left(−1,\frac{5}{2}\right)\) і\(\left(3,−\frac{3}{2}\right)\).
Крок 2 передбачає обчислення другої часткової похідної\(g\):
\[\begin{align*} g_{xx}(x,y) &=2x \\[4pt] g_{xy}(x,y) &=2\\[4pt] g_{yy}(x,y) &=2. \end{align*}\]
Потім знаходимо загальну формулу для\(D\):
\[\begin{align*} D(x_0, y_0) &=g_{xx}(x_0,y_0)g_{yy}(x_0,y_0)−\big(g_{xy}(x_0,y_0)\big)^2 \\[4pt] &=(2x_0)(2)−2^2\\[4pt] &=4x_0−4.\end{align*}\]
Далі підставляємо кожну критичну точку в цю формулу:
\[\begin{align*} D\left(−1,\tfrac{5}{2}\right) &=(2(−1))(2)−(2)^2=−4−4=−8 \\[4pt] D\left(3,−\tfrac{3}{2}\right) &=(2(3))(2)−(2)^2=12−4=8. \end{align*}\]
У кроці 3 ми зауважимо, що застосування Note to point\(\left(−1,\frac{5}{2}\right)\) призводить до випадку\(3\), що означає, що\(\left(−1,\frac{5}{2}\right)\) це точка сідла. Застосування теореми до точки\(\left(3,−\frac{3}{2}\right)\) призводить до випадку\(1\), що означає, що\(\left(3,−\frac{3}{2}\right)\) відповідає локальному мінімуму, як показано на наступному малюнку.

Використовуйте другий тест похідної, щоб знайти локальну крайність функції
\[ f(x,y)=x^3+2xy−6x−4y^2. \nonumber \]
- Підказка
-
Дотримуйтесь стратегії вирішення проблем для застосування другого похідного тесту.
- Відповідь
-
\(\left(\frac{4}{3},\frac{1}{3}\right)\)є точкою сідла,\(\left(−\frac{3}{2},−\frac{3}{8}\right)\) є локальним максимумом.
Абсолютні максими і мінімуми
При знаходженні глобальних екстремумів функцій однієї змінної на замкнутому інтервалі ми починаємо з перевірки критичних значень за цей інтервал, а потім оцінюємо функцію в кінцевих точках інтервалу. При роботі з функцією двох змінних замкнутий інтервал замінюється замкнутим, обмеженим множиною. Набір обмежується, якщо всі точки цієї множини можуть міститися в кулі (або диску) скінченного радіуса. Для початку нам потрібно знайти критичні точки всередині множини і обчислити відповідні критичні значення. Потім, необхідно знайти максимальне і мінімальне значення функції на межі множини. Коли ми маємо всі ці значення, найбільше значення функції відповідає глобальному максимуму, а найменше значення функції відповідає абсолютному мінімуму. По-перше, однак, ми повинні бути впевнені, що такі цінності існують. Наступна теорема робить це.
Неперервна функція\(f(x,y)\) на замкнутій та обмеженій множині\(D\) в площині досягає абсолютного максимального значення в певній точці\(D\) та абсолютного мінімуму в певній точці\(D\).
Тепер, коли ми знаємо, що будь-яка безперервна функція,\(f\) визначена на замкнутому обмеженому множині, досягає своїх крайніх значень, ми повинні знати, як їх знайти.
Припустимо,\(z=f(x,y)\) це диференційовна функція двох змінних, визначених на замкнутому обмеженому множині\(D\). Потім\(f\) досягне абсолютного максимального значення і абсолютного мінімуму, які є, відповідно, найбільшими і найменшими значеннями, знайденими серед наступних:
- Значення\(f\) в критичних точках\(f\) in\(D\).
- Значення\(f\) на кордоні\(D\).
Доказом цієї теореми є прямий наслідок теореми екстремальних значень і теореми Ферма. Зокрема, якщо будь-який екстремум не розташований на кордоні\(D\), то він розташовується у внутрішній точці\(D\). Але внутрішня точка\((x_0,y_0)\)\(D\) цього абсолютного екстремуму - це також локальний екстремум; отже,\((x_0,y_0)\) є критичною точкою теореми Ферма.\(f\) Тому єдиними можливими значеннями для глобальної екстремуми\(f\) на\(D\) є екстремальні значення\(f\) на внутрішній або межі\(D\).
\(z=f(x,y)\)Дозволяти бути безперервна функція двох змінних, визначених на замкнутому, обмеженому множині\(D\), і припустити, що\(f\) диференціюється на\(D\). Щоб знайти абсолютні максимальні і мінімальні значення\(f\) on\(D\), виконайте наступне:
- Визначте критичні точки\(f\) в\(D\).
- Обчисліть\(f\) в кожній з цих критичних точок.
- Визначте максимальне і\(f\) мінімальне значення на межі своєї області.
- Максимальне і мінімальне значення\(f\) буде відбуватися при одному з значень, отриманих в кроках\(2\) і\(3\).
Знайти максимальне і мінімальне значення\(f\) на кордоні\(D\) може бути складним завданням. Якщо межа являє собою прямокутник або набір прямих ліній, то можна параметризувати відрізки лінії і визначити максимуми на кожному з цих відрізків, як показано в прикладі\(\PageIndex{3}\). Такий же підхід можна використовувати для інших фігур, таких як кола та еліпси.
Якщо межа множини\(D\) є більш складною кривою, визначеною функцією\(g(x,y)=c\) для деякої константи\(c\), а частинними похідними першого порядку\(g\) exist, то метод множників Лагранжа може виявитися корисним для визначення екстремуми\(f\) на межі який вводиться в множників Лагранжа.
Використовувати стратегію розв'язання задач для знаходження абсолютних екстремумів функції для визначення абсолютних екстремумів кожної з наступних функцій:
- \(f(x,y)=x^2−2xy+4y^2−4x−2y+24\)на домені, визначеному\(0≤x≤4\) і\(0≤y≤2\)
- \(g(x,y)=x^2+y^2+4x−6y\)на домені, визначеному\(x^2+y^2≤16\)
Рішення
а. Використовуючи стратегію вирішення проблем, крок\(1\) передбачає знаходження критичних точок\(f\) на своїй області. Тому спочатку обчислюємо\(f_x(x,y)\) і\(f_y(x,y)\), потім ставимо їх кожен рівним нулю:
\[\begin{align*} f_x(x,y) &=2x−2y−4 \\[4pt] f_y(x,y) &=−2x+8y−2. \end{align*}\]
Встановлення їх рівних нулю дає систему рівнянь.
\[\begin{align*} 2x−2y−4 &=0\\[4pt] −2x+8y−2 &=0. \end{align*}\]
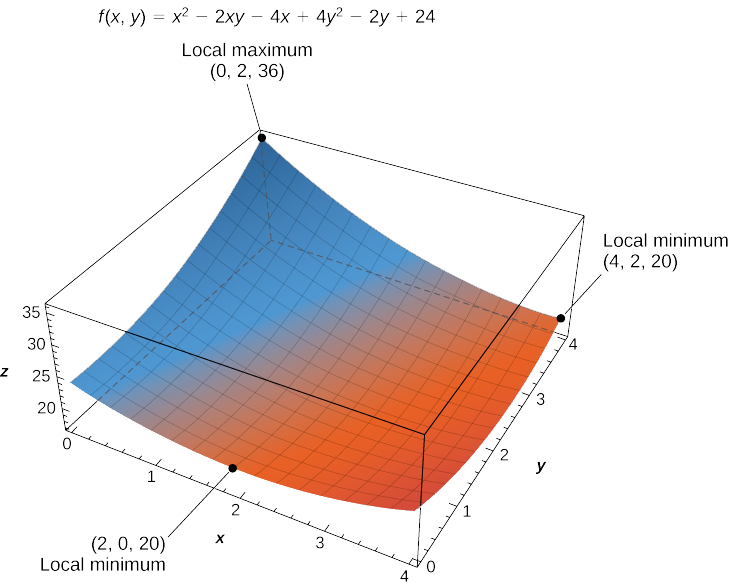
Рішенням цієї системи є\(x=3\) і\(y=1\). Тому\((3,1)\) є критичною точкою\(f\). Розрахунок\(f(3,1)\) дає\(f(3,1)=17.\)
Наступний крок передбачає знаходження крайності\(f\) на кордоні своєї області. Межа його області складається з чотирьох відрізків лінії, як показано на наступному графіку:

\(L_1\)це відрізок лінії\((4,0)\), що з'єднує\((0,0)\) і, і він може бути параметризований рівняннями\(x(t)=t,y(t)=0\) для\(0≤t≤4\). Визначте\(g(t)=f\big(x(t),y(t)\big)\). Це дає\(g(t)=t^2−4t+24\). Диференціація\(g\) призводить до\(g′(t)=2t−4.\) Тому\(g\) має критичне значення в\(t=2\), яке відповідає точці\((2,0)\). Обчислення\(f(2,0)\) дає\(z\) -значення\(20\).
\(L_2\)це відрізок лінії\((4,2)\), що з'єднує\((4,0)\) і, і він може бути параметризований рівняннями\(x(t)=4,y(t)=t\) для\(0≤t≤2.\) Знову, визначити\(g(t)=f\big(x(t),y(t)\big).\) Це дає\(g(t)=4t^2−10t+24.\) Тоді,\(g′(t)=8t−10\). g має критичне значення в\(t=\frac{5}{4}\), яке відповідає точці\(\left(0,\frac{5}{4}\right).\) Обчислення \(f\left(0,\frac{5}{4}\right)\)дає\(z\) -значення\(27.75\).
\(L_3\)це відрізок лінії\((4,2)\), що з'єднує\((0,2)\) і, і він може бути параметризований рівняннями\(x(t)=t,y(t)=2\) для\(0≤t≤4.\) Знову, визначити\(g(t)=f\big(x(t),y(t)\big).\) Це дає\(g(t)=t^2−8t+36.\) Критичне значення відповідає точці\((4,2).\) Отже, обчислення\(f(4,2)\) дає\(z\) -значення \(20\).
\(L_4\)це відрізок лінії\((0,2)\), що з'єднує\((0,0)\) і, і його можна параметризувати рівняннями\(x(t)=0,y(t)=t\) для\(0≤t≤2.\) цього часу,\(g(t)=4t^2−2t+24\) а критичне значення\(t=\frac{1}{4}\) відповідає точці\(\left(0,\frac{1}{4}\right)\). Обчислення\(f\left(0,\frac{1}{4}\right)\) дає значення\(z\) -value\(23.75.\)
Нам також потрібно знайти значення\(f(x,y)\) по кутах свого домену. Ці кути розташовуються за адресою\((0,0),(4,0),(4,2)\) і\((0,2)\):
\[\begin{align*} f(0,0) &=(0)^2−2(0)(0)+4(0)^2−4(0)−2(0)+24=24 \\[4pt] f(4,0) &=(4)^2−2(4)(0)+4(0)^2−4(4)−2(0)+24=24 \\[4pt] f(4,2) &=(4)^2−2(4)(2)+4(2)^2−4(4)−2(2)+24=20\\[4pt] f(0,2) &=(0)^2−2(0)(2)+4(2)^2−4(0)−2(2)+24=36. \end{align*}\]
Абсолютним максимальним значенням є\(36\)\((0,2)\), яке відбувається при, і глобальне мінімальне значення\(20\), яке зустрічається\((2,0)\) як\((4,2)\) і на наступному малюнку.
б. Використовуючи стратегію вирішення проблем, крок\(1\) передбачає знаходження критичних точок\(g\) на своїй області. Тому спочатку обчислюємо\(g_x(x,y)\) і\(g_y(x,y)\), потім ставимо їх кожен рівним нулю:
\[\begin{align*} g_x(x,y) &=2x+4 \\[4pt] g_y(x,y) &=2y−6. \end{align*}\]
Встановлення їх рівних нулю дає систему рівнянь.
\[\begin{align*} 2x+4 &=0 \\[4pt] 2y−6 &=0. \end{align*}\]
Рішенням цієї системи є\(x=−2\) і\(y=3\). Тому\((−2,3)\) є критичною точкою\(g\). Розрахунок\(g(−2,3),\) отримуємо
\[g(−2,3)=(−2)^2+3^2+4(−2)−6(3)=4+9−8−18=−13. \nonumber \]
Наступний крок передбачає знаходження крайності g на кордоні його області. Межа його області складається з окружності радіуса,\(4\) зосередженого на початку координат, як показано на наступному графіку.
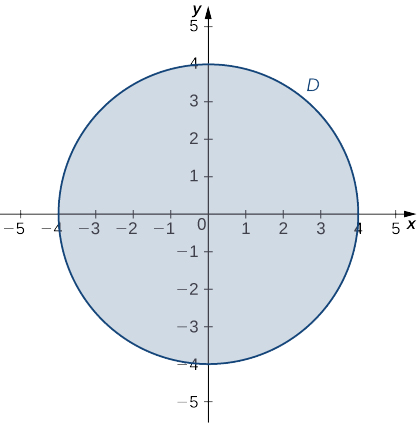
Межа області\(g\) може бути параметризована за допомогою функцій\(x(t)=4\cos t,\, y(t)=4\sin t\) для\(0≤t≤2π\). Визначте\(h(t)=g\big(x(t),y(t)\big):\)
\[\begin{align*} h(t) &=g\big(x(t),y(t)\big) \\[4pt] &=(4\cos t)^2+(4\sin t)^2+4(4\cos t)−6(4\sin t) \\[4pt] &=16\cos^2t+16\sin^2t+16\cos t−24\sin t\\[4pt] &=16+16\cos t−24\sin t. \end{align*}\]
Налаштування\(h′(t)=0\) призводить до
\[\begin{align*} −16\sin t−24\cos t &=0 \\[4pt] −16\sin t &=24\cos t\\[4pt] \dfrac{−16\sin t}{−16\cos t} &=\dfrac{24\cos t}{−16\cos t} \\[4pt] \tan t &=−\dfrac{3}{2}. \end{align*}\]
Це рівняння має два рішення за інтервал\(0≤t≤2π\). Один є,\(t=π−\arctan (\frac{3}{2})\) а інший є\(t=2π−\arctan (\frac{3}{2})\). Для першого кута,
\[\begin{align*} \sin t &=\sin(π−\arctan(\tfrac{3}{2}))=\sin (\arctan (\tfrac{3}{2}))=\dfrac{3\sqrt{13}}{13} \\[4pt] \cos t &=\cos (π−\arctan (\tfrac{3}{2}))=−\cos (\arctan (\tfrac{3}{2}))=−\dfrac{2\sqrt{13}}{13}. \end{align*}\]
Тому\(x(t)=4\cos t =−\frac{8\sqrt{13}}{13}\) і\(y(t)=4\sin t=\frac{12\sqrt{13}}{13}\), так\(\left(−\frac{8\sqrt{13}}{13},\frac{12\sqrt{13}}{13}\right)\) це критична точка на кордоні і
\[\begin{align*} g\left(−\tfrac{8\sqrt{13}}{13},\tfrac{12\sqrt{13}}{13}\right) &=\left(−\tfrac{8\sqrt{13}}{13}\right)^2+\left(\tfrac{12\sqrt{13}}{13}\right)^2+4\left(−\tfrac{8\sqrt{13}}{13}\right)−6\left(\tfrac{12\sqrt{13}}{13}\right) \\[4pt] &=\frac{144}{13}+\frac{64}{13}−\frac{32\sqrt{13}}{13}−\frac{72\sqrt{13}}{13} \\[4pt] &=\frac{208−104\sqrt{13}}{13}≈−12.844. \end{align*}\]
Для другого кута,
\[\begin{align*} \sin t &=\sin (2π−\arctan (\tfrac{3}{2}))=−\sin (\arctan (\tfrac{3}{2}))=−\dfrac{3\sqrt{13}}{13} \\[4pt] \cos t &=\cos (2π−\arctan (\tfrac{3}{2}))=\cos (\arctan (\tfrac{3}{2}))=\dfrac{2\sqrt{13}}{13}. \end{align*}\]
Тому\(x(t)=4\cos t=\frac{8\sqrt{13}}{13}\) і\(y(t)=4\sin t=−\frac{12\sqrt{13}}{13}\), так\(\left(\frac{8\sqrt{13}}{13},−\frac{12\sqrt{13}}{13}\right)\) це критична точка на кордоні і
\[\begin{align*} g\left(\tfrac{8\sqrt{13}}{13},−\tfrac{12\sqrt{13}}{13}\right) &=\left(\tfrac{8\sqrt{13}}{13}\right)^2+\left(−\tfrac{12\sqrt{13}}{13}\right)^2+4\left(\tfrac{8\sqrt{13}}{13}\right)−6\left(−\tfrac{12\sqrt{13}}{13}\right) \\[4pt] &=\dfrac{144}{13}+\dfrac{64}{13}+\dfrac{32\sqrt{13}}{13}+\dfrac{72\sqrt{13}}{13}\\[4pt] &=\dfrac{208+104\sqrt{13}}{13}≈44.844. \end{align*}\]
Абсолютний мінімум\(−13,\), який досягається в точці\((−2,3)\), яка є внутрішньою точкою\(D\).\(g\) Абсолютний максимум приблизно\(g\) дорівнює 44,844, що досягається в граничній точці\(\left(\frac{8\sqrt{13}}{13},−\frac{12\sqrt{13}}{13}\right)\). Це абсолютна крайність\(g\) on\(D\), як показано на наступному малюнку.
Використовувати стратегію розв'язання задач для знаходження абсолютних екстремумів функції для знаходження абсолютних екстремумів функції
\[f(x,y)=4x^2−2xy+6y^2−8x+2y+3 \nonumber \]
на домені, визначеному\(0≤x≤2\) і\(−1≤y≤3.\)
- Підказка
-
Обчисліть\(f_x(x,y)\) і\(f_y(x,y)\), і встановіть їх рівним нулю. Потім обчислити\(f\) для кожної критичної точки і знайти крайність\(f\) на межі\(D\).
- Відповідь
-
Абсолютний мінімум настає при\((1,0): f(1,0)=−1.\)
Абсолютний максимум настає при\((0,3): f(0,3)=63.\)
Pro-\(T\) компанія розробила модель прибутку, яка залежить від\(x\) кількості проданих м'ячів для гольфу в місяць (вимірюється тисячами), і кількості годин на місяць реклами\(y\), відповідно до функції
\[ z=f(x,y)=48x+96y−x^2−2xy−9y^2, \nonumber \]
де\(z\) вимірюється тисячами доларів. Максимальна кількість м'ячів для гольфу, які можна виробляти і продавати\(50,000\), є, і максимальна кількість годин реклами, які можна придбати\(25\). Знайдіть значення\(x\) і\(y\) які максимізують прибуток, і знайдіть максимальний прибуток.

Рішення
Використовуючи стратегію вирішення проблем, крок\(1\) передбачає знаходження критичних точок\(f\) на своїй області. Тому спочатку обчислюємо,\(f_x(x,y)\) а\(f_y(x,y),\) потім встановлюємо їх кожен рівним нулю:
\[\begin{align*} f_x(x,y) &=48−2x−2y \\[4pt] f_y(x,y) &=96−2x−18y. \end{align*}\]
Встановлення їх рівних нулю дає систему рівнянь.
\[\begin{align*} 48−2x−2y &=0 \\[4pt] 96−2x−18y &=0. \end{align*}\]
Рішенням цієї системи є\(x=21\) і\(y=3\). Тому\((21,3)\) є критичною точкою\(f\). Розрахунок\(f(21,3)\) дає\(f(21,3)=48(21)+96(3)−21^2−2(21)(3)−9(3)^2=648.\)
Домен цієї функції є\(0≤x≤50\) і\(0≤y≤25\) як показано на наступному графіку.
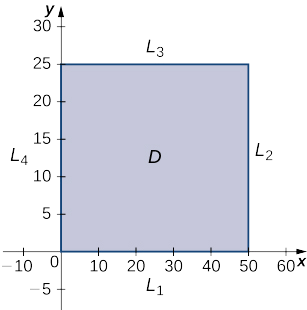
\(L_1\)це відрізок лінії, що з'єднує,\((0,0)\)\((50,0),\) і його можна параметризувати рівняннями\(x(t)=t,y(t)=0\) для\(0≤t≤50.\) Ми потім визначаємо\(g(t)=f(x(t),y(t)):\)
\[\begin{align*} g(t) &=f(x(t),y(t)) \\[4pt] &=f(t,0)\\[4pt] &=48t+96(0)−y^2−2(t)(0)−9(0)^2\\[4pt] &=48t−t^2. \end{align*}\]
Встановлення\(g′(t)=0\) дає критичну точку\(t=24,\), яка відповідає точці\((24,0)\) в області\(f\). Розрахунок\(f(24,0)\) дає\(576.\)
\(L_2\)це відрізок лінії\((50,25)\), що з'єднує\((50,0)\) і, і він може бути параметризований рівняннями\(x(t)=50,y(t)=t\) для\(0≤t≤25\). Ще раз визначаємо\(g(t)=f\big(x(t),y(t)\big):\)
\[\begin{align*} g(t) &=f\big(x(t),y(t)\big)\\[4pt] &=f(50,t)\\[4pt] &=48(50)+96t−50^2−2(50)t−9t^2 \\[4pt] &=−9t^2−4t−100. \end{align*}\]
Ця функція має критичну точку в\(t =−\frac{2}{9}\), яка відповідає точці\((50,−29)\). Цей пункт не знаходиться в області\(f\).
\(L_3\)це відрізок лінії\((50,25)\), що з'єднує\((0,25)\) і, і він може бути параметризований рівняннями\(x(t)=t,y(t)=25\) для\(0≤t≤50\). Визначаємо\(g(t)=f\big(x(t),y(t)\big)\):
\[\begin{align*} g(t) &=f\big(x(t),y(t)\big)\\[4pt] &=f(t,25) \\[4pt] &=48t+96(25)−t^2−2t(25)−9(25^2) \\[4pt] &=−t^2−2t−3225. \end{align*}\]
Ця функція має критичну точку в\(t=−1\), яка відповідає точці,\((−1,25),\) якої немає в області.
\(L_4\)це відрізок лінії\((0,25)\), що\((0,0)\) з'єднується з, і його можна параметризувати рівняннями\(x(t)=0,y(t)=t\) для\(0≤t≤25\). Визначаємо\(g(t)=f\big(x(t),y(t)\big)\):
\[\begin{align*} g(t) &=f\big(x(t),y(t)\big) \\[4pt] &=f(0,t) \\[4pt] &=48(0)+96t−(0)^2−2(0)t−9t^2 \\[4pt] &=96t−9t^2. \end{align*}\]
Ця функція має критичну точку в\(t=\frac{16}{3}\), яка відповідає точці\(\left(0,\frac{16}{3}\right)\), яка знаходиться на кордоні області. Розрахунок\(f\left(0,\frac{16}{3}\right)\) дає\(256\).
Нам також потрібно знайти значення\(f(x,y)\) по кутах свого домену. Ці кути розташовуються за адресою\((0,0),(50,0),(50,25)\) і\((0,25)\):
\[\begin{align*} f(0,0) &=48(0)+96(0)−(0)^2−2(0)(0)−9(0)^2=0\\[4pt] f(50,0) &=48(50)+96(0)−(50)^2−2(50)(0)−9(0)^2=−100 \\[4pt] f(50,25) &=48(50)+96(25)−(50)^2−2(50)(25)−9(25)^2=−5825 \\[4pt] f(0,25) &=48(0)+96(25)−(0)^2−2(0)(25)−9(25)^2=−3225. \end{align*}\]
Максимальне значення дорівнює\(648\), яке відбувається при\((21,3)\). Таким чином, максимальний прибуток\($648,000\) реалізується, коли м'ячі\(21,000\) для гольфу продаються і\(3\) годин реклами купуються на місяць, як показано на наступному малюнку.

Ключові поняття
- Критичною точкою функції\(f(x,y)\) є будь-яка точка\(f_x(x_0,y_0)=f_y(x_0,y_0)=0\),\((x_0,y_0)\) де або або хоча б одна з\(f_x(x_0,y_0)\) і\(f_y(x_0,y_0)\) не існує.
- Точка сідла - це точка\(f_x(x_0,y_0)=f_y(x_0,y_0)=0\),\((x_0,y_0)\) де, але не\(f(x_0,y_0)\) є ні максимумом, ні мінімумом в цій точці.
- Щоб знайти екстремуми функцій двох змінних, спочатку знайдіть критичні точки, потім обчислите дискримінант і застосуйте другий тест похідної.
Ключові рівняння
- Дискримінантний
\(D=f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)−(f_{xy}(x_0,y_0))^2\)
Глосарій
- критична точка функції двох змінних
-
точка\((x_0,y_0)\) називається критичною точкою,\(f(x,y)\) якщо дотримується одне з двох наступних умов:
1. \(f_x(x_0,y_0)=f_y(x_0,y_0)=0\)
2. Принаймні один з\(f_x(x_0,y_0)\) і\(f_y(x_0,y_0)\) не існує
- дискримінантний
- дискримінант функції\(f(x,y)\) задається формулою\(D=f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)−(f_{xy}(x_0,y_0))^2\)
- точка сідла
- з огляду\(z=f(x,y),\) на функцію точка\((x_0,y_0,f(x_0,y_0))\) є точкою сідла, якщо обидва\(f_x(x_0,y_0)=0\) і\(f_y(x_0,y_0)=0\), але\(f\) не має локального екстремуму при\((x_0,y_0)\)
