12.8: Глава 12 Огляд вправ
- Page ID
- 61554
Для вправ 1 - 4 визначте, чи є твердження істинним або хибним. Обгрунтуйте відповідь доказом або зустрічнимприкладом.
1) Для векторів\(\vecs a\) і\(\vecs b\) і будь-якого заданого скаляра\( c, \, c(\vecs a⋅\vecs b)=(c\vecs a)⋅\vecs b.\)
- Відповідь
- Правда; Див. Доказ у розділі 11.3
2) Для векторів\(\vecs a\) і\(\vecs b\) і будь-якого заданого скаляра\( c, \, c(\vecs a×\vecs b)=(c\vecs a)×\vecs b\).
3) Симетричне рівняння для лінії перетину між двома площинами\( x+y+z=2\) і\( x+2y−4z=5\) задається\( −\frac{x−1}{6}=\frac{y−1}{5}=z.\)
- Відповідь
- False, перетворюючи симетричні рівняння вище в параметричні рівняння прямої, отримуємо:
\(x = 1 - 6t\)
\(y = 1 + 5t\)
\(z = t\)
Якщо ця лінія лежить на кожній площині, ми повинні отримати тотожність (як 5 = 5), коли ми підставити кожний вираз\(t\) у рівняння кожної площини.
Підставляючи в першу площину рівняння, ми отримуємо:\( (1-6t) + (1+5t) + t = 2\,\checkmark\)
Таким чином, ми знаємо, що ця лінія дійсно лежить на першій площині.
Але коли ми підставляємо рівняння другої площини, ми отримуємо:\( (1 - 6t) + 2(1 + 5t) - 4(t) = 1 - 6t + 2 + 10t - 4t = 3 \neq 5\)
Оскільки ми не отримуємо ідентичність, ми знаємо, що ця лінія не знаходиться на другій площині і тому не може бути лінією перетину дві площини.
4) Якщо\(\vecs a⋅\vecs b=0,\) то\(\vecs a\) перпендикулярно\(\vecs b\).
- Відповідь
- False, так як\(\vecs a\) або\(\vecs b\) може бути також нульовим вектором.
Для вправ 5 і 6 використовуйте задані вектори, щоб знайти величини.
5)\(\vecs a=9\hat{\mathbf{i}}−2\hat{\mathbf{j}},\quad \vecs b=−3\hat{\mathbf{i}}+\hat{\mathbf{k}}\)
а.\( 3\vecs a+\vecs b\)
б.\( \|\vecs a\|\)
c.\(\vecs a×\|\vecs b×\vecs a\|\)
д.\( \|\vecs b×\vecs a\|\)
- Відповідь
- a.\( ⟨24,−6, 1⟩\)
b.\( \sqrt{85}\)
c. Не вдається перетнути вектор зі скаляром
d.\( 11\)
6)\(\vecs a=2\hat{\mathbf{i}}+\hat{\mathbf{j}}−9\hat{\mathbf{k}},\quad \vecs b=−\hat{\mathbf{i}}+2\hat{\mathbf{k}},\quad \vecs c=4\hat{\mathbf{i}}−2\hat{\mathbf{j}}+\hat{\mathbf{k}}\)
а.\( 2\vecs a−\vecs b\)
б.\( \|\vecs b×\vecs c\|\)
c.\( \vecs b×\left(\vecs b×\vecs c\right)\)
д.\( \vecs c×\|\vecs b×\vecs a\|\)
е.\( \text{Proj}_\vecs{a}\vecs b\)
7) Знайти значення\(a\) таких, що вектори\( ⟨2,4,a⟩\) і\( ⟨0,−1,a⟩\) є ортогональними.
- Відповідь
- \( a=±2\)
Для вправ 8 і 9 знайдіть одиничні вектори.
8) Знайдіть одиничний вектор, який має той самий напрямок,\(\vecs v\) що і вектор, який починається\( (0,−3)\) і закінчується\( (4,10).\)
9) Знайдіть одиничний вектор, який має той самий напрямок,\(\vecs v\) що і вектор, який починається\( (1,4,10)\) і закінчується\( (3,0,4).\)
- Відповідь
- \( ⟨\frac{1}{\sqrt{14}},−\frac{2}{\sqrt{14}},−\frac{3}{\sqrt{14}}⟩ = ⟨\frac{\sqrt{14}}{14},−\frac{\sqrt{14}}{7},−\frac{3\sqrt{14}}{14}⟩ \)
Для вправ 10 і 11 знайдіть площу або обсяг заданих фігур.
10) Паралелограм, що охоплюється векторами\(\vecs a=⟨1,13⟩\) і\(\vecs b=⟨3,21⟩\)
11) Паралелепіпед, утворений\(\vecs a=⟨1,4,1⟩\) і\(\vecs b=⟨3,6,2⟩,\) і\(\vecs c=⟨−2,1,−5⟩\)
- Відповідь
- \( 27\)одиниць\(^2\)
Для вправ 12 і 13 знайдіть параметричні рівняння і векторне рівняння прямої з заданими властивостями.
12) Лінія, яка проходить через точку\( (2,−3,7)\), паралельну вектору\( ⟨1,3,−2⟩\)
13) Лінія, яка проходить через точки\( (1,3,5)\) і\( (−2,6,−3)\)
- Відповідь
- \( x=1−3t,y=3+3t,z=5−8t,\quad \vecs r(t)=(1−3t)\hat{\mathbf{i}}+3(1+t)\hat{\mathbf{j}}+(5−8t)\hat{\mathbf{k}}\)
Для вправ 14 і 15 знайдіть рівняння площини з заданими властивостями.
14) Площина, яка проходить через точку\( (4,7,−1)\) і має нормальний вектор\(\vecs n=⟨3,4,2⟩\)
15) Площина, яка проходить через точки\( (0,1,5),(2,−1,6),\) і\( (3,2,5).\)
- Відповідь
- \( −x+3y+8z=43\)
Для вправ 16 і 17 знайдіть сліди для поверхонь в площинами\( x=k,y=k\), а\( z=k.\) потім, опишіть і намалюйте поверхні.
16)\( 9x^2+4y^2−16y+36z^2=20\)
17)\( x^2=y^2+z^2\)
- Відповідь
- \( x=k\)trace:\( k^2=y^2+z^2\) коло,\( y=k\) трасування:\( x^2−z^2=k^2\) є гіперболою (або парою рядків, якщо\( k=0), z=k\) trace:\( x^2−y^2=k^2\) є гіперболою (або парою рядків, якщо\( k=0\)). Поверхня являє собою конус.
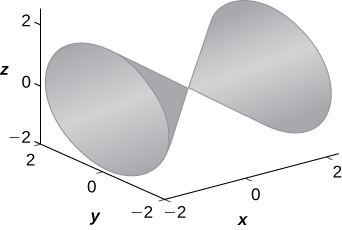
Для вправ 18 і 19 запишіть задане рівняння в циліндричних координатах і сферичних координатах.
18)\( x^2+y^2+z^2=144\)
19)\( z=x^2+y^2−1\)
- Відповідь
- Циліндричні:\( z=r^2−1,\) сферичні:\( \cos φ=ρ\sin^2 φ−\frac{1}{ρ}\)
Для вправ 20 і 21 перетворіть задані рівняння з циліндричних або сферичних координат в прямокутні координати. Визначте задану поверхню.
20)\( ρ^2(\sin^2(φ)−\cos^2(φ))=1\)
21)\( r^2−2r\cos(θ)+z^2=1\)
- Відповідь
- \( x^2−2x+y^2+z^2=1\), сфера
Для вправ 22 і 23 розгляньте невеликий човен, що перетинає річку.
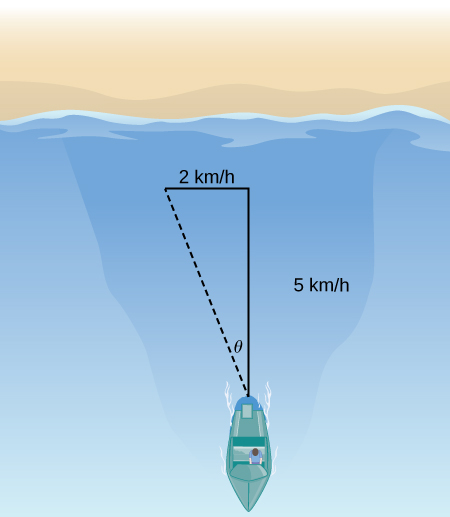
22) Якщо швидкість човна\( 5\) км/год обумовлена північністю в негазованій воді, а вода має струм\( 2\) км/год через захід (див. Наступний малюнок), яка швидкість човна щодо берега? Який кут,\( θ\) що човен насправді подорожує?
23) Коли човен досягає берега, людям кидають дві мотузки, щоб допомогти витягнути човен на берег. Одна мотузка знаходиться під кутом,\( 25°\) а інша - під\( 35°\). Якщо човен потрібно тягнути прямо і з силою\( 500\) N, знайдіть величину сили для кожної мотузки (див. Наступний малюнок).
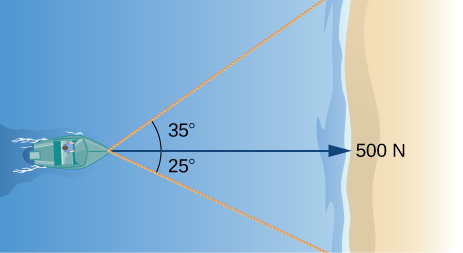
- Відповідь
- 331 Н і 244 Н
24) Літак летить у напрямку 52° на схід від півночі зі швидкістю 450 км/год. Сильний вітер має підшипник 33° на схід від півночі зі швидкістю 50 миль/год. Яка результуюча швидкість землі та підшипник літака?
25) Обчисліть виконану роботу переміщенням частинки з положення\( (1,2,0)\) в\( (8,4,5)\) уздовж прямої з силою\(\vecs F=2\hat{\mathbf{i}}+3\hat{\mathbf{j}}−\hat{\mathbf{k}}.\)
- Відповідь
- \( 15\)J
У задачах 26 і 27 розгляньте вашу невдалу спробу зняти шину з вашого автомобіля за допомогою гайкового ключа, щоб послабити болти. Припустимо, що гайковий ключ довжиною\( 0.3\) м, і ви в змозі застосувати силу 200-Н.
26) Оскільки ваша шина спущена, ви можете застосувати свою силу лише\( 60°\) під кутом. Який крутний момент в центрі болта? Припустимо, цього зусилля недостатньо, щоб послабити болт.
27) Хтось позичає вам домкрат для шин, і тепер ви можете застосувати силу 200-N\( 80°\) під кутом. Ваш результуючий крутний момент буде більш-менш? Який новий отриманий крутний момент в центрі болта? Припустимо, цього зусилля недостатньо, щоб послабити болт.
- Відповідь
- Більше,\( 59.09\) Дж
