11.4: Площа та довжина дуги в полярних координатах

Цілі навчання

• Застосуйте формулу для площі області в полярних координатах.
• Визначте довжину дуги полярної кривої.

У прямокутній системі координат певний інтеграл забезпечує спосіб обчислення площі під кривою. Зокрема, якщо у нас є функція,\(y=f(x)\) визначена\(x=b\) звідки\(x=a\)\(f(x)>0\) на цьому інтервалі, площа між кривою та віссю x задається

\[A=\int ^b_af(x)dx. \nonumber \]

Цей факт разом з формулою оцінки цього інтеграла узагальнено в Фундаментальній теоремі числення. Аналогічно довжина дуги цієї кривої задається

\[L=\int ^b_a\sqrt{1+(f′(x))^2}dx. \nonumber \]

У цьому розділі ми вивчаємо аналогічні формули для площі та довжини дуги в полярній системі координат.

Області областей, обмежених полярними кривими

Досліджено формули для площі під кривою, визначеною у прямокутних координатах та параметрично визначених кривих. Тепер звернемо увагу на виведення формули для площі області, обмеженої полярною кривою. Нагадаємо, що доказ фундаментальної теореми числення використовував поняття суми Рімана для наближення площі під кривою за допомогою прямокутників. Для полярних кривих ми знову використовуємо суму Рімана, але прямокутники замінюються секторами кола.

Розглянемо криву, визначену функцією,\(r=f(θ),\) де\(α≤θ≤β.\) Нашим першим кроком є поділ інтервалу\([α,β]\) на n суб-інтервалів рівної ширини. Ширина кожного підінтервалу задається формулою\(Δθ=(β−α)/n\), а i\(θ_i\) - точка розбиття задається формулою\(θ_i=α+iΔθ\). Кожна точка розділу\(θ=θ_i\) визначає лінію з нахилом,\(\tan θ_i\) що проходить через полюс, як показано на наступному графіку.

Малюнок\(\PageIndex{1}\): Розділ типової кривої в полярних координатах.

Відрізки лінії з'єднуються дугами постійного радіуса. Це визначає сектори, площі яких можна обчислити за допомогою геометричної формули. Потім площа кожного сектора використовується для наближення площі між послідовними відрізками лінії. Потім ми підсумовуємо площі секторів, щоб наблизити загальну площу. Такий підхід дає наближення суми Рімана для загальної площі. Формула площі сектора кола проілюстрована на наступному малюнку.

Малюнок\(\PageIndex{2}\): Площа сектора кола задається значенням\(A=\dfrac{1}{2}θr^2\).

Нагадаємо, що площа кола є\(A=πr^2\). При вимірюванні кутів в радіанах 360 градусів дорівнює\(2π\) радіанам. Тому частку кола можна виміряти центральним кутом\(θ\). Дробу кола задано\(\dfrac{θ}{2π}\), тому площа сектора - це цей дріб, помножений на загальну площу:

\[A=(\dfrac{θ}{2π})πr^2=\dfrac{1}{2}θr^2. \nonumber \]

Оскільки радіус типового сектора на малюнку\(\PageIndex{1}\) задається\(r_i=f(θ_i)\), площа i го сектора задається

\[A_i=\dfrac{1}{2}(Δθ)(f(θ_i))^2. \nonumber \]

Тому сума Рімана, яка наближає площу, задається

\[A_n=\sum_{i=1}^nA_i≈\sum_{i=1}^n\dfrac{1}{2}(Δθ)(f(θ_i))^2. \nonumber \]

Беремо ліміт,\(n→∞\) щоб отримати точну площу:

\[A=\lim_{n→∞}A_n=\dfrac{1}{2}\int ^β_α(f(θ))^2dθ. \nonumber \]

Це дає наступну теорему.

Площа області, обмеженої полярною кривою

Припустимо\(f\), є безперервним і невід'ємним на інтервалі\(α≤θ≤β\) с\(0<β−α≤2π\). Площа області обмежена графіком\(r=f(θ)\) між радіальними лініями\(θ=α\) і\(θ=β\) дорівнює

\[\begin{align} A =\dfrac{1}{2}\int ^β_α[f(θ)]^2 dθ \\[4pt] =\dfrac{1}{2}\int ^β_αr^2 dθ. \label{areapolar}\end{align} \]

Приклад\(\PageIndex{1}\): Finding an Area of a Polar Region

Знайти площу однієї пелюстки троянди, визначену рівнянням\(r=3\sin(2θ).\)

Рішення

Графік наведено\(r=3\sin (2θ)\) нижче.

Малюнок\(\PageIndex{3}\): Графік\(r=3\sin (2θ).\)

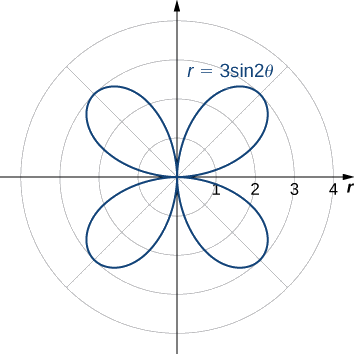
Коли у\(θ=0\) нас є\(r=3\sin(2(0))=0\). Наступне значення, для якого\(r=0\) є\(θ=π/2\). У цьому можна переконатися, вирішивши рівняння\(3\sin (2θ)=0\) для\(θ\). Тому значення\(θ=π/2\) слід\(θ=0\) простежити за першою пелюсткою троянди. Щоб знайти площу всередині цієї пелюстки, використовуйте Equation\ ref {areapolar} з\(f(θ)=3\sin (2θ), α=0,\) і\(β=π/2\):

\[\begin{align*} A &=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ \\[4pt] &=\dfrac{1}{2}\int ^{π/2}_0[3\sin (2θ)]^2dθ \\[4pt] &=\dfrac{1}{2}\int ^{π/2}_09\sin^2(2θ)dθ. \end{align*}\]

Щоб оцінити цей інтеграл, скористайтеся формулою\(\sin^2α=(1−\cos (2α))/2\) з\(α=2θ:\)

\[\begin{align*} A &=\dfrac{1}{2}\int ^{π/2}_09\sin^2(2θ)dθ \\[4pt] &=\dfrac{9}{2}\int ^{π/2}_0\dfrac{(1−\cos(4θ))}{2}dθ \\[4pt] &=\dfrac{9}{4}(\int ^{π/2}_01−\cos(4θ)dθ) \\[4pt] &=\dfrac{9}{4}(θ−\dfrac{\sin(4θ)}{4}∣^{π/2}_0 \\[4pt] &=\dfrac{9}{4}(\dfrac{π}{2}−\dfrac{\sin 2π}{4})−\dfrac{9}{4}(0−\dfrac{\sin 4(0)}{4}) \\[4pt] &=\dfrac{9π}{8}\end{align*}\]

Вправа\(\PageIndex{1}\)

Знайдіть площу всередині кардіоїда, визначену рівнянням\(r=1−\cos θ\).

Підказка

Використовуйте рівняння\ ref {areapolar}. Обов'язково перед оцінкою визначте правильні межі інтеграції.

Відповідь

\(A=3π/2\)

Приклад\(\PageIndex{1}\) передбачав знаходження області всередині однієї кривої. Ми також можемо використовувати Equation\ ref {areapolar}, щоб знайти площу між двома полярними кривими. Однак нам часто потрібно знайти точки перетину кривих і визначити, яка функція визначає зовнішню криву або внутрішню криву між цими двома точками.

Приклад\(\PageIndex{2}\): Finding the Area between Two Polar Curves

Знайдіть область за межами кардіоїда\(r=2+2\sin θ\) і всередині кола\(r=6\sin θ\).

Рішення

Спочатку намалюйте графік, що містить обидві криві, як показано на малюнку.

Малюнок\(\PageIndex{4}\): Область між кривими\(r=2+2\sin θ\) і\(r=6\sin θ.\)

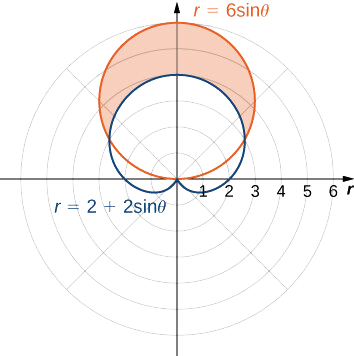
Щоб визначити межі інтеграції, спочатку знайдіть точки перетину, встановивши дві рівні один одному функції і вирішивши для\(θ\):

\[\begin{align*} 6 \sin θ &=2+2\sin θ \\[4pt] 4\sin θ &=2 \\[4pt] \sin θ &=\dfrac{1}{2} \end{align*}. \nonumber \]

Це дає рішення\(θ=\dfrac{π}{6}\) і\(θ=\dfrac{5π}{6}\), які є межею інтеграції. Коло\(r=3\sin θ\) - це червоний графік, який є зовнішньою функцією, а кардіоїд\(r=2+2\sin θ\) - синій графік, який є внутрішньою функцією. Щоб обчислити площу між кривими, почніть з площі всередині кола між\(θ=\dfrac{π}{6}\) і\(θ=\dfrac{5π}{6}\), потім відніміть площу всередині кардіоїда між\(θ=\dfrac{π}{6}\) і\(θ=\dfrac{5π}{6}\):

\(A=\text{circle}−\text{cardioid}\)

\(=\dfrac{1}{2}\int ^{5π/6}_{π/6}[6\sin θ]^2dθ−\dfrac{1}{2}\int ^{5π/6}_{π/6}[2+2\sin θ]^2dθ\)

\(=\dfrac{1}{2}\int ^{5π/6}_{π/6}36\sin^2θ\,dθ−\dfrac{1}{2}\int ^{5π/6}_{π/6}4+8\sin θ+4\sin^2θ\,dθ\)

\(=18\int ^{5π/6}_{π/6}\dfrac{1−\cos(2θ)}{2}dθ−2\int ^{5π/6}_{π/6}1+2\sin θ+\dfrac{1−\cos(2θ)}{2}dθ\)

\(=9[θ−\dfrac{\sin(2θ)}{2}]^{5π/6}_{π/6}−2[\dfrac{3θ}{2}−2\cos θ−\dfrac{\sin(2θ)}{4}]^{5π/6}_{π/6}\)

\(=9(\dfrac{5π}{6}−\dfrac{\sin(10π/6)}{2})−9(\dfrac{π}{6}−\dfrac{\sin(2π/6)}{2})−(3(\dfrac{5π}{6})−4\cos\dfrac{5π}{6}−\dfrac{\sin(10π/6)}{2})+(3(\dfrac{π}{6})−4\cos\dfrac{π}{6}−\dfrac{\sin(2π/6)}{2})\)

\(=4π\).

Вправа\(\PageIndex{2}\)

Знайдіть область всередині кола\(r=4\cos θ\) і поза колом\(r=2\).

Підказка

Використовуйте Equation\ ref {areapolar} і скористайтеся перевагами симетрії.

Відповідь

\(A=\dfrac{4π}{3}+2\sqrt{3}\)

У прикладі\(\PageIndex{2}\) ми знайшли область всередині кола і поза кардіоїдом, спочатку знайшовши їх точки перетину. Зверніть увагу, що рішення рівняння безпосередньо\(θ\) для дало два рішення:\(θ=\dfrac{π}{6}\) і\(θ=\dfrac{5π}{6}\). Однак на графіку є три точки перетину. Третя точка перетину - це початок. Причина, чому ця точка не відображається як рішення, полягає в тому, що походження знаходиться на обох графіках, але для різних значень\(θ\). Наприклад, за кардіоїд ми отримуємо

\[\begin{align*} 2+2\sin θ =0 \\[4pt] \sin θ =−1 ,\end{align*}. \nonumber \]

так\(θ\) що значення для цього вирішити це рівняння є\(θ=\dfrac{3π}{2}+2nπ\), де\(n\) є будь-яке ціле число. Для кола отримуємо

\[6\sin θ=0. \nonumber \]

Розв'язки цього рівняння мають вигляд\(θ=nπ\) для будь-якого цілого значення\(n\). Ці два набори рішень не мають спільних точок. Незалежно від цього факту криві перетинаються біля початку. Цей випадок завжди потрібно враховувати.

Довжина дуги в полярних кривих

Тут ми виведемо формулу довжини дуги кривої, визначеної в полярних координатах. У прямокутних координатах довжина дуги параметризованої кривої\((x(t),y(t))\) для\(a≤t≤b\) задається

\[L=\int ^b_a\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}dt. \nonumber \]

У полярних координатах ми визначаємо криву рівнянням\(r=f(θ)\), де Для\(α≤θ≤β.\) того, щоб адаптувати формулу довжини дуги для полярної кривої, використовуємо рівняння

\[x=r\cos θ=f(θ)\cos θ \nonumber \]

і

\[y=r\sin θ=f(θ)\sin θ, \nonumber \]

і замінюємо параметр\(t\) на\(θ\). Тоді

\[\dfrac{dx}{dθ}=f′(θ)\cos θ−f(θ)\sin θ \nonumber \]

\[\dfrac{dy}{dθ}=f′(θ)\sin θ+f(θ)\cos θ. \nonumber \]

Замінюємо\(dt\) на\(dθ\), а нижня і верхня межі інтеграції є\(α\) і\(β\), відповідно. Тоді формула довжини дуги стає

\[ \begin{align*} L &=\int ^b_a\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt \\[4pt] &=\int ^β_α\sqrt{\left(\dfrac{dx}{dθ}\right)^2+\left(\dfrac{dy}{dθ}\right)^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ)\cos θ−f(θ)\sin θ)^2+(f′(θ)\sin θ+f(θ)\cos θ)^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ))^2(\cos^2 θ+\sin^2 θ)+(f(θ))^2(\cos^2 θ+\sin^2θ)}\,dθ \\[4pt] &=\int ^β_α\sqrt{(f′(θ))^2+(f(θ))^2}\,dθ \\[4pt] &=\int ^β_α\sqrt{r^2+\left(\dfrac{dr}{dθ}\right)^2}\,dθ \end{align*}\]

Це дає нам наступну теорему.

Довжина дуги кривої, визначеної полярною функцією

\(f\)Дозволяти функція, похідна якої є неперервною на інтервалі\(α≤θ≤β\). Довжина графіка\(r=f(θ)\) від\(θ=α\) до\(θ=β\) дорівнює

\[ \begin{align} L &=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}\,dθ \label{arcpolar1} \\[4pt] &=\int ^β_α\sqrt{r^2+\left(\dfrac{dr}{dθ}\right)^2}\,dθ. \label{arcpolar2} \end{align} \]

Приклад\(\PageIndex{3}\): Finding the Arc Length of a cardioid

Знайти довжину дуги кардіоїда\(r=2+2\cos θ\).

Рішення

Коли\(θ=0,r=2+2\cos 0 =4.\) Крім того, як\(θ\) йде від\(0\) до\(2π\), кардіоїд простежується рівно один раз. Тому це межі інтеграції. Використання\(f(θ)=2+2\cos θ, α=0,\) і\(β=2π,\) рівняння\ ref {arcpolar1} стає

\[\begin{align*} L &=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{[2+2\cos θ]^2+[−2\sin θ]^2}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{4+8\cos θ+4\cos^2θ+4\sin^2θ}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{4+8\cos θ+4(\cos^2θ+\sin^2θ)}\,dθ \\[4pt] &=\int ^{2π}_0\sqrt{8+8\cos θ}\,dθ \\[4pt] &=2\int ^{2π}_0\sqrt{2+2\cos θ}\,dθ. \end{align*}\]

Далі за допомогою ідентичності\(\cos(2α)=2\cos^2α−1,\) додайте 1 в обидві сторони і помножте на 2. Це дає\(2+2\cos(2α)=4\cos^2α.\) Заміна\(α=θ/2\) дає\(2+2\cos θ=4\cos^2(θ/2)\), тому інтеграл стає

\[\begin{align*} L &= 2\int ^{2π}_0\sqrt{2+2\cos θ}\,dθ \\[4pt] &=2\int ^{2π}_0\sqrt{4\cos^2(\dfrac{θ}{2})}\,dθ \\[4pt] &=4\int ^{2π}_0∣\cos(\dfrac{θ}{2})∣\,dθ.\end{align*}\]

Абсолютне значення необхідно, оскільки косинус є від'ємним для деяких значень у своїй області. Щоб вирішити цю проблему, змініть\(0\) ліміти з на\(π\) і подвоїти відповідь. Ця стратегія працює, оскільки косинус позитивний між\(0\) і\(\dfrac{π}{2}\). Таким чином,

\[\begin{align*} L &=4\int ^{2π}_0∣\cos(\dfrac{θ}{2})∣\,dθ \\[4pt] &=8\int ^π_0 \cos(\dfrac{θ}{2})\,dθ \\[4pt] &=8(2\sin(\dfrac{θ}{2})∣^π_0 \\[4pt] &=16\end{align*}\]

Вправа\(\PageIndex{3}\)

Знайти загальну довжину дуги\(r=3\sin θ\).

Підказка

Використовуйте рівняння\ ref {arcpolar1}. Щоб визначити правильні межі, складіть таблицю значень.

Відповідь

\(s=3π\)

Ключові поняття

• Площа області в полярних координатах, визначених рівнянням\(r=f(θ)\) с\(α≤θ≤β\), задається інтегралом\(A=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ\).
• Щоб знайти площу між двома кривими в полярній системі координат, спочатку знайдіть точки перетину, потім відніміть відповідні ділянки.
• Довжина дуги полярної кривої, визначеної рівнянням\(r=f(θ)\) з,\(α≤θ≤β\) задається інтегралом\(L=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}dθ=\int ^β_α\sqrt{r^2+(\dfrac{dr}{dθ})^2}dθ\).

Ключові рівняння

• Площа області, обмеженої полярною кривою\[A=\dfrac{1}{2}\int ^β_α[f(θ)]^2dθ=\dfrac{1}{2}\int ^β_αr^2dθ \nonumber \]
• Довжина дуги полярної кривої\[L=\int ^β_α\sqrt{[f(θ)]^2+[f′(θ)]^2}dθ=\int ^β_α\sqrt{r^2+(\dfrac{dr}{dθ})^2}dθ \nonumber \]