11.3: Полярні координати
- Page ID
- 61738
- Знайдіть точки на площині за допомогою полярних координат.
- Перетворення точок між прямокутними і полярними координатами.
- Намалюйте полярні криві з даних рівнянь.
- Перетворення рівнянь між прямокутними та полярними координатами.
- Визначте симетрію в полярних кривих і рівняннях.
Прямокутна система координат (або декартова площина) забезпечує засіб відображення точок до впорядкованих пар і впорядкованих пар до точок. Це називається відображенням один до одного від точок у площині до впорядкованих пар. Полярна система координат забезпечує альтернативний метод відображення точок на впорядковані пари. У цьому розділі ми бачимо, що за деяких обставин полярні координати можуть бути кориснішими, ніж прямокутні координати.
Визначення полярних координат
Щоб знайти координати точки в полярній системі координат, розглянемо рис\(\PageIndex{1}\). Точка\(P\) має декартові координати\((x,y)\). Відрізок лінії, що з'єднує початок з точкою,\(P\) вимірює відстань від початку до\(P\) і має довжину\(r\). Кут між позитивною віссю x та відрізком лінії має міру\(θ\). Це спостереження говорить про природну відповідність між координатною парою\((x,y)\) і значеннями\(r\) і\(θ\). Ця відповідність є основою полярної системи координат. Зверніть увагу, що кожна точка декартової площини має два значення (звідси термін впорядкована пара), пов'язаних з нею. У полярній системі координат кожна точка також має два значення, пов'язані з нею:\(r\) і\(θ\).
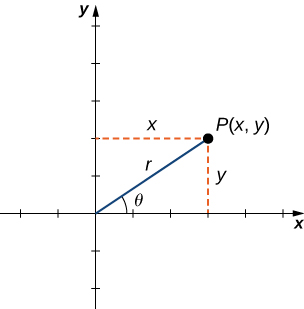
Використовуючи тригонометрію прямокутника, для точки вірні наступні рівняння\(P\):
\[\cos θ=\dfrac{x}{r}\text{ so }x=r\cos θ \nonumber \]
\[\sin θ=\dfrac{y}{r}\text{ so }y=r\sin θ. \nonumber \]
Крім того,
\[r^2=x^2+y^2 \nonumber \]
і
\[\tan θ=\dfrac{y}{x}. \nonumber \]
Тому кожна точка\((x,y)\) декартової системи координат може бути представлена у вигляді впорядкованої пари\((r,θ)\) в полярній системі координат. Перша координата називається радіальною координатою, а друга - кутовою координатою. Кожна точка на площині може бути представлена в такому вигляді.
Зауважте, що рівняння\(\tan θ=y/x\) має нескінченну кількість розв'язків для будь-якої впорядкованої пари\((x,y)\). Однак, якщо ми обмежимо розв'язки значеннями між\(0\) і\(2π\) тоді ми можемо призначити унікальне рішення квадранту, в якому\((x,y)\) знаходиться вихідна точка. Тоді відповідне значення\(r\) позитивне, так\(r^2=x^2+y^2\).
Враховуючи точку\(P\) на площині з декартовими координатами\((x,y)\) та полярними координатами\((r,θ)\), такі формули перетворення мають значення:
\[\begin{align} x &=r\cos θ \label{eq1} \\[4pt] y &=r\sin θ \label{eq2}\end{align} \]
і
\[\begin{align} r^2 &= x^2+y^2 \label{eq3}\\[4pt] \tan θ &=\dfrac{y}{x} \label{eq4}\end{align}. \]
Ці формули можуть бути використані для перетворення з прямокутних в полярні або від полярних до прямокутних координат. Зверніть увагу, що рівняння\ ref {eq3} є теоремою Піфагора. (Малюнок\(\PageIndex{1}\)).
Перетворіть кожну з наступних точок у полярні координати.
- \((1,1)\)
- \((−3,4)\)
- \((0,3)\)
- \((5\sqrt{3},−5)\)
Перетворіть кожну з наступних точок у прямокутні координати.
- \((3,π/3)\)
- \((2,3π/2)\)
- \((6,−5π/6)\)
Рішення
a. використовувати\(x=1\) і\(y=1\) в рівнянні\ ref {eq3}:
\[\begin{align*} r^2 &=x^2+y^2 \\[4pt] &=1^2+1^2 \\ r &=\sqrt{2} \end{align*} \nonumber \]
і через рівняння\ ref {eq4}
\[\begin{align*} \tan θ &= \dfrac{y}{x} = \dfrac{1}{1}=1 \\[4pt] θ &=\dfrac{π}{4}. \end{align*}\]
Тому цю точку можна представити\((\sqrt{2},\dfrac{π}{4})\) у вигляді полярних координат.
б. використовувати\(x=−3\) і\(y=4\) в рівнянні\ ref {eq3}:
\[\begin{align*} r^2 &= x^2+y^2=(−3)^2+(4)^2 \\[4pt] r&=5 \end{align*}\]
і через рівняння\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=−\dfrac{4}{3}\)
\(θ=\arctan(-\dfrac{4}{3})+π≈2.21.\)
Тому цю точку можна представити\((5,2.21)\) у вигляді полярних координат.
c. використовувати\(x=0\) і\(y=3\) в рівнянні\ ref {eq3}:
\(r^2=x^2+y^2=(3)^2+(0)^2=9+0\)\(r=3\)
і через рівняння\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=\dfrac{3}{0}\).
Пряме застосування другого рівняння призводить до ділення на нуль. Графік точки\((0,3)\) на прямокутній системі координат показує, що точка розташована на позитивній осі Y. Кут між позитивною віссю x та позитивною віссю y дорівнює\(\dfrac{π}{2}\). Тому цю точку можна представити\((3,\dfrac{π}{2})\) у вигляді полярних координат.
d Використовувати\(x=5\sqrt{3}\) і\(y=−5\) в рівнянні\ ref {eq3}:
\(r^2=x^2+y^2=(5\sqrt{3})^2+(−5)^2=75+25\)
\(r=10\)
і через рівняння\ ref {eq4}
\(\tan θ=\dfrac{y}{x}=\dfrac{−5}{5\sqrt{3}}=−\dfrac{\sqrt{3}}{3}\)
\(θ=−\dfrac{π}{6}\).
Тому цю точку можна представити\((10,−\dfrac{π}{6})\) у вигляді полярних координат.
e Використовувати\(r=3\) і\(θ=\dfrac{π}{3}\) в рівнянні\ ref {eq1}:
\(x=r\cos θ=3\cos(\dfrac{π}{3})=3(\dfrac{1}{2})=\dfrac{3}{2}\)
і
\(y=r\sin θ=3\sin(\dfrac{π}{3})=3(\dfrac{\sqrt{3}}{2})=\dfrac{3\sqrt{3}}{2}\).
Тому цю точку можна представити\((\dfrac{3}{2},\dfrac{3\sqrt{3}}{2})\) у вигляді прямокутних координат.
f Використовувати\(r=2\) і\(θ=\dfrac{3π}{2}\) в рівнянні\ ref {eq1}:
\(x=r\cos θ=2\cos(\dfrac{3π}{2})=2(0)=0\)
і
\(y=r\sin θ=2\sin(\dfrac{3π}{2})=2(−1)=−2.\)
Тому цю точку можна представити\((0,−2)\) у вигляді прямокутних координат.
g Використовувати\(r=6\) і\(θ=−\dfrac{5π}{6}\) в рівнянні\ ref {eq1}:
\(x=r\cos θ=6\cos(−\dfrac{5π}{6})=6(−\dfrac{\sqrt{3}}{2})=−3\sqrt{3}\)
і
\(y=r\sin θ=6\sin(−\dfrac{5π}{6})=6(−\dfrac{1}{2})=−3\).
Тому цю точку можна представити\((−3\sqrt{3},−3)\) у вигляді прямокутних координат.
Перетворення\((−8,−8)\) в полярні координати і\((4,\dfrac{2π}{3})\) в прямокутні координати.
- Підказка
-
Використовуйте рівняння\ ref {eq3} і рівняння\ ref {eq1}. Обов'язково перевіряйте квадрант при розрахунку\(θ\).
- Відповідь
-
\((8\sqrt{2},\dfrac{5π}{4})\)і\((−2,2\sqrt{3})\)
Полярне представлення точки не є унікальним. Наприклад, полярні координати\((2,\dfrac{π}{3})\) і\((2,\dfrac{7π}{3})\) обидва представляють точку\((1,\sqrt{3})\) в прямокутній системі. Також значення r може бути від'ємним. Тому точка з полярними координатами\((−2,\dfrac{4π}{3})\) також представляє точку\((1,\sqrt{3})\) в прямокутній системі, як ми бачимо за допомогою Equation\ ref {eq1}:
\[x=r\cos θ=−2\cos(\dfrac{4π}{3})=−2(−\dfrac{1}{2})=1 \nonumber \]
і
\[y=r\sin θ=−2\sin(\dfrac{4π}{3})=−2(−\dfrac{\sqrt{3}}{2})=\sqrt{3}. \nonumber \]
Кожна точка на площині має нескінченну кількість зображень у полярних координатах. Однак кожна точка на площині має лише одне уявлення в прямокутній системі координат.
Зверніть увагу, що полярне зображення точки в площині також має візуальну інтерпретацію. Зокрема,\(r\) це спрямована відстань, яку точка лежить від початку, і\(θ\) вимірює кут, який відрізок лінії від початку до точки робить з позитивною\(x\) -віссю. Позитивні кути вимірюються в напрямку проти годинникової стрілки, а негативні - за годинниковою стрілкою. Полярна система координат відображається на рисунку\(\PageIndex{2}\).
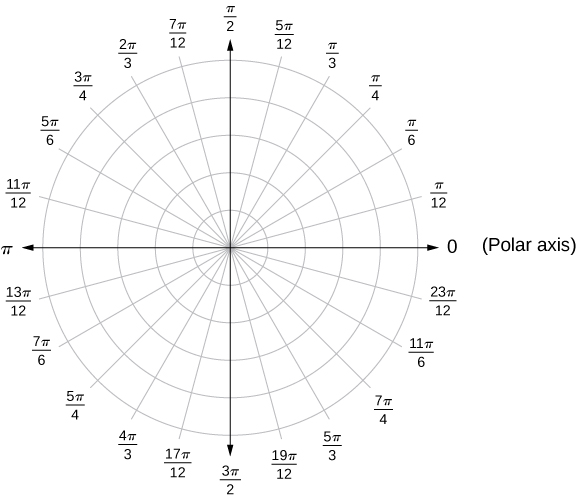
Відрізок лінії, що починається від центру графіка, що йде вправо (називається позитивною віссю x в декартовій системі), є полярною віссю. Центральна точка є полюсом, або початком, системи координат, і відповідає\(r=0\). Сама внутрішня окружність, показана на малюнку,\(\PageIndex{2}\) містить всі точки на відстані 1 одиниці від полюса, і представлена рівнянням\(r=1\). Потім\(r=2\) йде набір точок 2 одиниці від полюса і так далі. Відрізки лінії, що виходять від полюса, відповідають фіксованим кутам. Для побудови точки в полярній системі координат почніть з кута. Якщо кут позитивний, то виміряйте кут від полярної осі в напрямку проти годинникової стрілки. Якщо він негативний, то вимірюйте його за годинниковою стрілкою. Якщо значення r позитивне, перемістіть цю відстань уздовж кінцевого променя кута. Якщо він негативний, рухайтеся уздовж променя, який знаходиться навпроти кінцевого променя заданого кута.
Покладіть кожну з наступних точок на полярній площині.
- \((2,\dfrac{π}{4})\)
- \((−3,\dfrac{2π}{3})\)
- \((4,\dfrac{5π}{4})\)
Рішення
Три точки побудовані на малюнку\(\PageIndex{3}\).

Ділянка\((4,\dfrac{5π}{3})\) і\((−3,−\dfrac{7π}{2})\) на полярній площині.
- Підказка
-
Почніть з\(θ\), потім використовуйте\(r\).
- Відповідь
-

Полярні криві
Тепер, коли ми знаємо, як побудувати точки в полярній системі координат, ми можемо обговорити, як побудувати криві. У прямокутній системі координат ми можемо намалювати функцію\(y=f(x)\) та створити криву в декартовій площині. Аналогічним чином ми можемо графікувати криву, яка генерується функцією\(r=f(θ)\).
Загальна ідея графікування функції в полярних координатах така ж, як графікування функції в прямокутних координатах. Почніть зі списку значень незалежної змінної (\(θ\)в даному випадку) і обчислите відповідні значення залежної змінної\(r\). Цей процес генерує список впорядкованих пар, які можуть бути побудовані в полярній системі координат. Нарешті, з'єднайте точки і скористайтеся будь-якими візерунками, які можуть з'явитися. Функція може бути періодичною, наприклад, що вказує на те, що для незалежної змінної потрібна лише обмежена кількість значень.
- Створіть таблицю з двома стовпцями. Перший стовпець - for\(θ\), а другий стовпець - для\(r\).
- Створіть список значень для\(θ\).
- Обчисліть відповідні\(r\) значення для кожного\(θ\).
- Покладіть кожну\((r,θ)\) впорядковану пару на осях координат.
- З'єднайте точки і шукайте викрійку.
Графік кривої, визначеної функцією\(r=4\sin θ\). Визначте криву і перепишіть рівняння в прямокутні координати.
Рішення
Оскільки функція кратна синусоїдальної функції, вона є періодичною з періодом\(2π\), тому використовуйте значення для\(θ\) між\(0\) і\(2π\). Результат кроків 1—3 відображається в наступній таблиці. \(\PageIndex{4}\)На малюнку показаний графік, заснований на цій таблиці.
| \(θ\) | \(r=4\sin θ\) | \(θ\) | \(r=4\sin θ\) |
|---|---|---|---|
| \ (θ\)» style="вертикальне вирівнювання: середина; "> 0 | \ (r=4\ sin θ\)» стиль = "вертикальне вирівнювання: середина; "> 0 | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(π\) | \ (r=4\ sin θ\)» стиль = "вертикальне вирівнювання: середина; "> 0 |
| \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{π}{6}\) | \ (r=4\ sin θ\)» стиль = "вертикальне вирівнювання: середина; "> 2 | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{7π}{6}\) | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; ">\(-2\) |
| \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{π}{4}\) | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; ">\(2\sqrt{2}≈2.8\) | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{5π}{4}\) | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; ">\(−2\sqrt{2}≈−2.8\) |
| \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{π}{3}\) | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; ">\(2\sqrt{3}≈3.4\) | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{4π}{3}\) | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; ">\(−2\sqrt{3}≈−3.4\) |
| \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{π}{2}\) | \ (r=4\ sin θ\)» стиль = "вертикальне вирівнювання: середина; "> 4 | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3π}{2}\) | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; ">\(-4\) |
| \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{2π}{3}\) | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; ">\(2\sqrt{3}≈3.4\) | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{5π}{3}\) | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; ">\(−2\sqrt{3}≈−3.4\) |
| \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3π}{4}\) | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; ">\(2\sqrt{2}≈2.8\) | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{7π}{4}\) | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; ">\(−2\sqrt{2}≈−2.8\) |
| \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{5π}{6}\) | \ (r=4\ sin θ\)» стиль = "вертикальне вирівнювання: середина; "> 2 | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{11π}{6}\) | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; ">−2 |
| \ (θ\)» style="вертикальне вирівнювання: середина; "> | \ (r=4\ sin θ\)» style="вертикальне вирівнювання: середина; "> | \ (θ\)» style="вертикальне вирівнювання: середина; ">\(2π\) | \ (r=4\ sin θ\)» стиль = "вертикальне вирівнювання: середина; "> 0 |
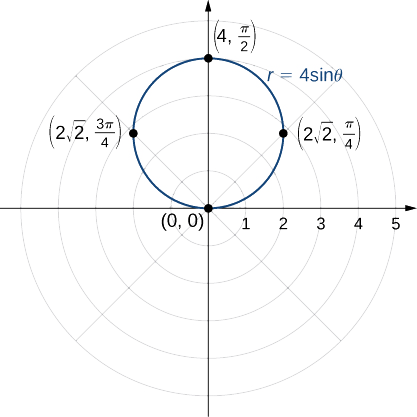
Це графік кола. Рівняння\(r=4\sin θ\) можна перетворити в прямокутні координати, попередньо помноживши обидві сторони на\(r\). Це дає рівняння\(r^2=4r\sin θ.\) Далі використовувати факти, які\(r^2=x^2+y^2\) і\(y=r\sin θ\). Це дає\(x^2+y^2=4y\). Щоб поставити це рівняння в стандартну форму, відніміть\(4y\) з обох сторін рівняння і заповніть квадрат:
\[\begin{align*} x^2+y^2−4y &= 0 \\[4pt] x^2+(y^2−4y) &= 0 \\[4pt] x^2+(y^2−4y+4) &= 0+4 \\[4pt] x^2+(y−2)^2&=4 \end{align*}\]
Це рівняння кола з радіусом 2 і центром\((0,2)\) в прямокутній системі координат.
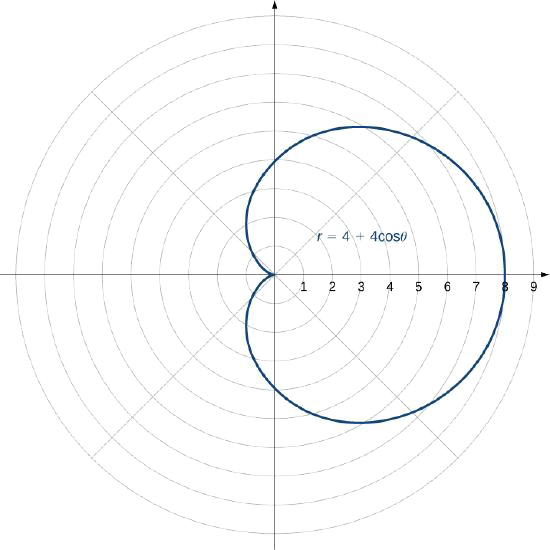
Створіть графік кривої, визначеної функцією\(r=4+4\cos θ\).
- Підказка
-
Дотримуйтесь стратегії вирішення проблем для створення графа в полярних координатах.
- Відповідь
-
Назва цієї форми - кардіоїдна, яку ми вивчимо далі в цьому розділі.
Графік\(\PageIndex{3}\) у прикладі - це коло. Рівняння кола можна перетворити в прямокутні координати за допомогою формул перетворення координат в Equation\ ref {eq1}. У прикладі\(\PageIndex{4}\) наведено кілька прикладів функцій для перетворення з полярних до прямокутних координат.
Перепишіть кожне з наступних рівнянь в прямокутних координатах і визначте графік.
- \(θ=\dfrac{π}{3}\)
- \(r=3\)
- \(r=6\cos θ−8\sin θ\)
Рішення:
а. візьміть тангенс обох сторін. Це дає\(\tan θ=\tan(π/3)=\sqrt{3}\) .Оскільки\(\tan θ=y/x\) ми можемо замінити ліву частину цього рівняння на\(y/x\). Це дає\(y/x=\sqrt{3}\), який можна переписати як\(y=x\sqrt{3}\). Це рівняння прямої, що проходить через початок з нахилом\(\sqrt{3}\). Взагалі, будь-яке полярне рівняння виду\(θ=K\) являє собою пряму лінію через полюс з нахилом, рівним\(\tan K\).
б. по-перше, квадрат обидві сторони рівняння. Це дає\(r^2=9.\) Next\(r^2\) замінити на\(x^2+y^2\). Це дає рівняння\(x^2+y^2=9\), яке є рівнянням окружності з центром у початку з радіусом 3. Загалом, будь-яке полярне рівняння виду,\(r=k\) де k - додатна константа, являє собою коло радіуса k з центром у початку. (Примітка: при квадратизації обох сторін рівняння можна ненавмисно вводити нові точки. Це завжди слід враховувати. Однак в даному випадку ми не вводимо нових пунктів. Наприклад,\((−3,\dfrac{π}{3})\) це та ж точка, що і\((3,\dfrac{4π}{3})\).)
c Помножити обидві сторони рівняння на\(r\). Це призводить до\(r^2=6r\cos θ−8r\sin θ\). Далі використовуйте формули
\(r^2=x^2+y^2,x=r\cos θ,y=r\sin θ.\)
Це дає
\(r^2=6(r\cos θ)−8(r\sin θ)\)
\(x^2+y^2=6x−8y.\)
Щоб поставити це рівняння в стандартну форму, спочатку перемістіть змінні з правого боку рівняння в ліву сторону, потім завершіть квадрат.
\(x^2+y^2=6x−8y\)
\(x^2−6x+y^2+8y=0\)
\((x^2−6x)+(y^2+8y)=0\)
\((x^2−6x+9)+(y^2+8y+16)=9+16\)
\((x−3)^2+(y+4)^2=25.\)
Це рівняння кола з центром в\((3,−4)\) і радіусом 5. Зверніть увагу, що коло проходить через початок, оскільки центр знаходиться на відстані 5 одиниць.
Перепишіть рівняння\(r=\sec θ\tan θ\) в прямокутних координатах і визначте його графік.
- Підказка
-
Перетворити на синус і косинус, потім помножити обидві сторони на косинус.
- Відповідь
-
\(y=x^2\), Що є рівнянням параболи, що відкривається вгору.
Зараз ми бачили кілька прикладів малювання графіків кривих, визначених полярними рівняннями. Короткий опис деяких загальних кривих наведено в таблицях нижче. У кожному рівнянні a і b - довільні константи.
Кардіоїд - це особливий випадок limaçon (вимовляється «лі-мах-сон»), в якому\(a=b\) або\(a=−b\). Троянда це дуже цікава крива. Зверніть увагу, що графік\(r=3\sin 2θ\) має чотири пелюстки. Однак графік\(r=3\sin 3θ\) має три пелюстки, як показано на малюнку.
Якщо коефіцієнт\(θ\) парний, графік має вдвічі більше пелюсток, ніж коефіцієнт. Якщо коефіцієнт\(θ\) непарний, то кількість пелюсток дорівнює коефіцієнту. Вам рекомендується вивчити, чому це відбувається. Ще більш цікаві графіки з'являються, коли коефіцієнт не\(θ\) є цілим числом. Наприклад, якщо раціонально, то крива замкнута; тобто вона в кінцевому підсумку закінчується там, де почалася (рис.\(\PageIndex{8a}\)). Однак якщо коефіцієнт нераціональний, то крива ніколи не замикається (рис.\(\PageIndex{8b}\)). Хоча може здатися, що крива замкнута, при уважному розгляді виявляється, що пелюстки трохи вище позитивної осі x трохи товщі. Це пояснюється тим, що пелюстка не зовсім збігається з початковою точкою.
Оскільки крива, визначена графіком\(r=3\sin(πθ)\) ніколи не замикається, крива, зображена на малюнку,\(\PageIndex{8b}\) є лише частковим зображенням. По суті, це приклад кривої заповнення простору. Крива заповнення простору - це та, яка фактично займає двовимірну підмножину реальної площини. У цьому випадку крива займає коло радіуса 3 з центром у початковій точці.
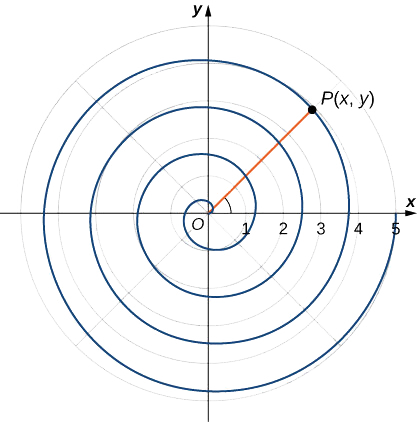
Нагадаємо, патерний наутілус, введений в главі прелюдії. Ця істота відображає спіраль, коли половина зовнішньої оболонки відрізана. Можна описати спіраль за допомогою прямокутних координат. \(\PageIndex{9}\)На малюнку зображена спіраль в прямокутних координатах. Як ми можемо описати цю криву математично?
Рішення
Коли точка P рухається навколо спіралі в напрямку проти годинникової стрілки, її відстань d від початку збільшується. Припустімо, що відстань d є постійною кратною k кута\(θ\), який робить відрізок лінії OP з додатною віссю x. Тому\(d(P,O)=kθ\),\(O\) де походження. Тепер скористайтеся формулою відстані і деякою тригонометрією:
\(d(P,O)=kθ\)
\(\sqrt{(x−0)^2+(y−0)^2}=k\arctan(\dfrac{y}{x})\)
\(\sqrt{x^2+y^2}=k\arctan(\dfrac{y}{x})\)
\(\arctan(\dfrac{y}{x})=\dfrac{\sqrt{x^2+y^2}}{k}\)
\(y=x\tan(\dfrac{\sqrt{x^2+y^2}}{k})\).
Хоча це рівняння описує спіраль, неможливо вирішити його безпосередньо ні для x, ні y, однак, якщо ми використовуємо полярні координати, рівняння стає набагато простішим. Зокрема\(d(P,O)=r\), і\(θ\) є другою координатою. Тому рівняння для спіралі стає\(r=kθ\). Зверніть увагу, що коли\(θ=0\) ми також маємо\(r=0\), так спіраль виходить від походження. Ми можемо зняти це обмеження, додавши константу до рівняння. Тоді рівняння для спіралі стає\(r=a+kθ\) для довільних констант\(a\) і\(k\). Це називається Архімедова спіраль, на честь грецького математика Архімеда.
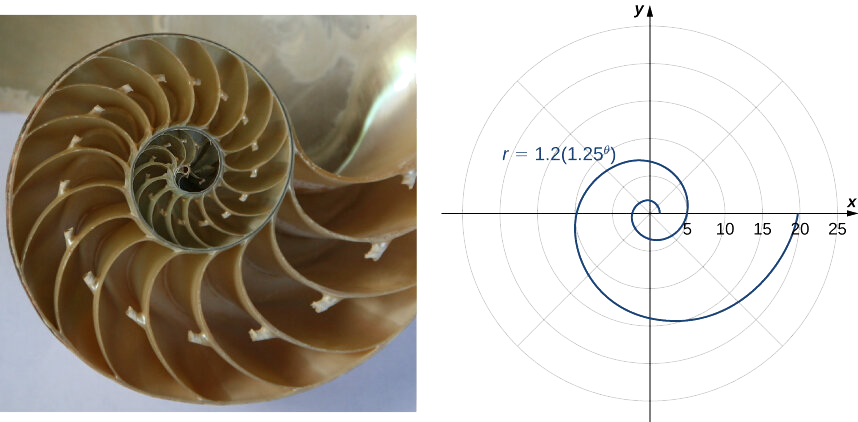
Інший тип спіралі - логарифмічна спіраль, описана функцією\(r=a⋅b^θ\). Графік функції\(r=1.2(1.25^θ)\) наведено на рисунку\(\PageIndex{10}\). Ця спіраль описує форму раковини патерного наутілуса.
Припустимо, що крива описується в полярній системі координат за допомогою функції\(r=f(θ)\). Оскільки у нас є формули перетворення з полярних до прямокутних координат, заданих
\[x=r\cos θ \nonumber \]
\[y=r\sin θ \nonumber \],
можна переписати ці формули за допомогою функції
\[x=f(θ)\cos θ \nonumber \]
\[y=f(θ)\sin θ. \nonumber \]
Цей крок дає параметризацію кривої в прямокутних координатах, використовуючи в\(θ\) якості параметра. Наприклад, формула спіралі\(r=a+bθ\) з малюнка стає
\[x=(a+bθ)\cos θ \nonumber \]
\[y=(a+bθ)\sin θ. \nonumber \]
Допускаючи\(θ\) діапазон від\(−∞\) до\(∞\) генерує всю спіраль.
Симетрія в полярних координатах
При вивченні симетрії функцій в прямокутних координатах (тобто у вигляді\(y=f(x)\)) ми говоримо про симетрію щодо осі y і симетрії щодо початку. Зокрема, якщо\(f(−x)=f(x)\) для всіх\(x\) в області\(f\), то\(f\) є парна функція і її графік симетричний по відношенню до осі y. Якщо\(f(−x)=−f(x)\) для всіх x в області\(f\), то f - непарна функція, а її графік симетричний щодо походження. Визначивши, які типи симетрії проявляє графік, ми можемо дізнатися більше про форму і зовнішній вигляд графіка. Симетрія також може виявити інші властивості функції, яка генерує графік. Аналогічним чином працює симетрія в полярних кривих.
Розглянемо криву,\(r=f(θ)\) породжену функцією в полярних координатах.
- Крива симетрична щодо полярної осі, якщо для кожної точки\((r,θ)\) на графіку точка також\((r,−θ)\) знаходиться на графіку. Аналогічно рівняння\(r=f(θ)\) незмінне шляхом\(θ\) заміни на\(−θ\).
- Крива симетрична щодо полюса, якщо для кожної точки\((r,θ)\) на графіку точка також\((r,π+θ)\) знаходиться на графіку. Аналогічно рівняння\(r=f(θ)\) незмінне\(r\) при заміні на\(−r\), або\(θ\) з\(π+θ.\)
- Крива симетрична щодо вертикальної лінії,\(θ=\dfrac{π}{2}\) якщо для кожної точки\((r,θ)\) на графіку точка також\((r,π−θ)\) знаходиться на графіку. Аналогічно\(r=f(θ)\) рівняння незмінне\(θ\) при заміні на\(π−θ\).
У наступній таблиці наведені приклади кожного типу симетрії.
Знайдіть симетрію троянди, визначену рівнянням,\(r=3\sin(2θ)\) і створіть графік.
Рішення
Припустимо\((r,θ)\), точка знаходиться на графіку\(r=3\sin(2θ).\)
i. щоб перевірити на симетрію навколо полярної осі, спочатку спробуйте\(θ\) замінити на\(−θ\). Це дає\(r=3\sin(2(−θ))=−3\sin(2θ)\). Оскільки це змінює вихідне рівняння, цей тест не задовольняється. Однак, повертаючись до вихідного рівняння і замінивши на\(−r\) і\(r\)\(θ\) з\(π−θ\) врожайністю
\[ \begin{align*} −r&=3\sin(2(π−θ)) \\[4pt] −r &=3\sin(2π−2θ) \\[4pt] −r &=3\sin(−2θ) \\[4pt] −r &=−3\sin2θ. \end{align*}\]
Множення обох сторін цього рівняння на\(−1\) дає\(r=3\sin 2θ\), що є вихідним рівнянням. Це демонструє, що графік симетричний щодо полярної осі.
II. Щоб перевірити на симетрію по відношенню до полюса, спочатку\(r\) замініть на\(−r\), який дає\(−r=3\sin(2θ)\). Множення обох сторін на\(−1\) дає\(r=−3\sin(2θ)\), що не узгоджується з вихідним рівнянням. Тому рівняння не проходить тест на цю симетрію. Однак повернення до вихідного рівняння і\(θ\) заміна на\(θ+π\) дає
\[ \begin{align*} r&=3\sin(2(θ+π)) \\[4pt] &=3\sin(2θ+2π) \\[4pt] &=3(\sin 2θ \cos 2π + \cos 2θ \sin 2π) \\[4pt] &=3\sin 2θ. \end{align*}\]
Оскільки це узгоджується з вихідним рівнянням, графік симетричний щодо полюса.
III. Щоб перевірити симетрію щодо вертикальної лінії\(θ=\dfrac{π}{2}\), спочатку замініть обидва на\(−r\) і\(r\)\(θ\) з\(−θ\).
\[ \begin{align*} −r &=3\sin(2(−θ)) \\[4pt] −r &=3\sin(−2θ) \\[4pt] −r &=−3 \sin 2θ. \end{align*}\]
Множення обох сторін цього рівняння на\(−1\) дає\(r=3\sin 2θ\), що є вихідним рівнянням. Тому графік симетричний щодо вертикальної лінії\(θ=\dfrac{π}{2}\).
Цей графік має симетрію щодо полярної осі, початку та вертикальної лінії, що проходить через полюс. Для побудови графіка функції складіть в таблицю значень\(θ\) між,\(0\)\(π/2\) а потім відобразіть отриманий графік.
| 0 | 0 |
| \(\dfrac{π}{6}\) | \(\dfrac{3\sqrt{3}}{2}≈2.6\) |
| \(\dfrac{π}{4}\) | 3 |
| \(\dfrac{π}{3}\) | \(\dfrac{3\sqrt{3}}{2}≈2.6\) |
| \(\dfrac{π}{2}\) | 0 |
Це дає один пелюстка троянди, як показано на наступному графіку.
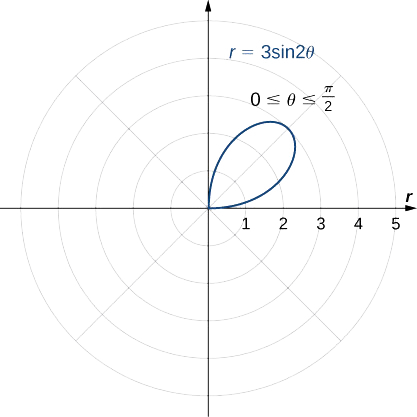
Відображення цього зображення в інших трьох квадрантах дає весь графік, як показано на малюнку.
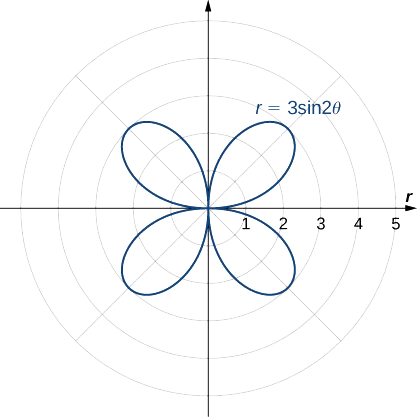
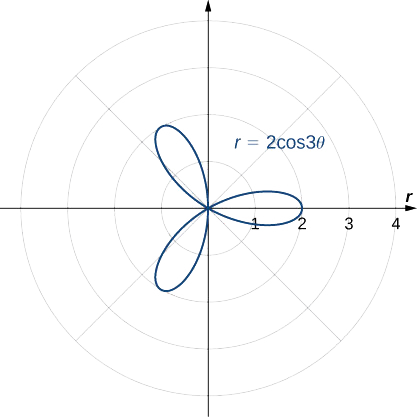
Визначте симетрію графіка, визначеного рівнянням,\(r=2\cos(3θ)\) і створіть графік.
- Підказка
-
Використовуйте Примітку.
- Відповідь
-
Симетричний щодо полярної осі.
Ключові концепції
- Полярна система координат забезпечує альтернативний спосіб розташування точок на площині.
- Перетворення точок між прямокутними і полярними координатами за допомогою формул
\[x=r\cos θ \text{ and } y=r\sin θ \nonumber \]
і
\[r=\sqrt{x^2+y^2} \text{ and} \tan θ=\dfrac{y}{x}. \nonumber \]
- Щоб намалювати полярну криву з заданої полярної функції, складіть таблицю значень і скористайтеся періодичними властивостями.
- Використовуйте формули перетворення для перетворення рівнянь між прямокутними та полярними координатами.
- Визначте симетрію в полярних кривих, які можуть відбуватися через полюс, горизонтальну вісь або вертикальну вісь.
Глосарій
- кутова координата
- \(θ\)кут, утворений відрізком лінії, що з'єднує початок з точкою в полярній системі координат з позитивною радіальною (x) віссю, виміряною проти годинникової стрілки
- кардіоїдних
- плоска крива простежується точкою по периметру кола, яка рухається навколо фіксованого кола того ж радіуса; рівняння кардіоїдних є\(r=a(1+\sin θ)\) або\(r=a(1+\cos θ)\)
- Лімасон
- графік рівняння\(r=a+b\sin θ\) або\(r=a+b\cos θ.\) Якщо\(a=b\) тоді графік кардіоїдний
- полярна вісь
- горизонтальна вісь у полярній системі координат, що відповідає\(r≥0\)
- полярна система координат
- система розташування точок в площині. Координати є\(r\), радіальна координата та\(θ\) кутова координата
- полярне рівняння
- рівняння або функція, що стосуються радіальної координати з кутовою координатою в полярній системі координат
- полюс
- центральна точка полярної системи координат, еквівалентна початку декартової системи
- радіальна координата
- \(r\)координата в полярній системі координат, яка вимірює відстань від точки в площині до полюса
- троянда
- графік полярного рівняння\(r=a\cos 2θ\) або\(r=a\sin 2θ\) для додатної константи\(a\)
- крива заповнення простору
- крива, яка повністю займає двовимірну підмножину реальної площини
