11.2: Обчислення параметричних кривих

Last updated
Save as PDF

Page ID: 61696

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте похідні та рівняння тангенсів для параметричних кривих.
Знайдіть площу під параметричною кривою.
Використовуйте рівняння для довжини дуги параметричної кривої.
Застосуйте формулу площі поверхні до об'єму, створеного параметричною кривою.

Тепер, коли ми ввели поняття параметризованої кривої, наш наступний крок - навчитися працювати з цим поняттям в контексті числення. Наприклад, якщо нам відома параметризація заданої кривої, чи можна обчислити нахил дотичної лінії до кривої? Як щодо довжини дуги кривої? Або площа під кривою?

Інший сценарій: Припустимо, ми хотіли б представити місце розташування бейсболу після того, як м'яч залишає руку глечика. Якщо положення бейсболу представлено площиною кривої,$(x(t),y(t))$ то ми повинні мати можливість використовувати обчислення, щоб знайти швидкість м'яча в будь-який момент часу. Крім того, ми повинні бути в змозі обчислити, наскільки далеко цей м'яч пройшов як функція часу.

Похідні параметричних рівнянь

Ми почнемо з питання, як обчислити нахил прямої дотичної до параметричної кривої в точці. Розглянемо плоску криву, визначену параметричними рівняннями

\[\begin{align} x(t) &=2t+3 \label{eq1} \\ y(t) &=3t−4 \label{eq2} \end{align} \]

всередині$−2≤t≤3$.

Графік цієї кривої відображається на рисунку$\PageIndex{1}$. Це відрізок лінії, що починається$(−1,−10)$ і закінчується на$(9,5).$

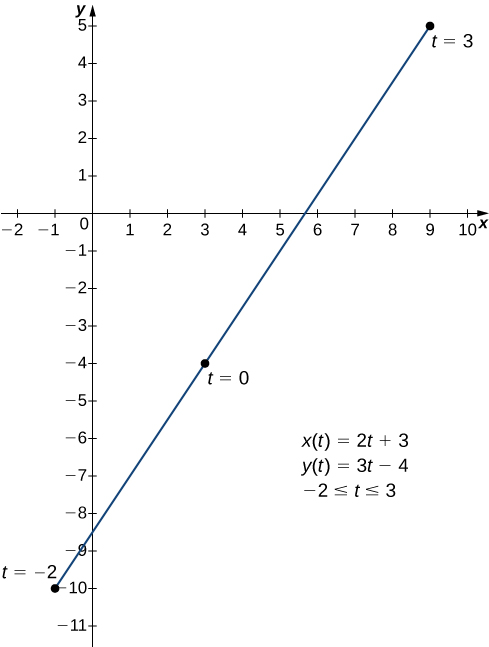
Ми можемо усунути параметр, попередньо розв'язавши Equation\ ref {eq1} для$t$:

$x(t)=2t+3$

$x−3=2t$

$t=\dfrac{x−3}{2}$.

Підставивши це в$y(t)$ (Equation\ ref {eq2}), отримаємо

$y(t)=3t−4$

$y=3\left(\dfrac{x−3}{2}\right)−4$

$y=\dfrac{3x}{2}−\dfrac{9}{2}−4$

$y=\dfrac{3x}{2}−\dfrac{17}{2}$.

Нахил цієї лінії задається по$\dfrac{dy}{dx}=\dfrac{3}{2}$. Далі розраховуємо$x′(t)$ і$y′(t)$. Це дає$x′(t)=2$ і$y′(t)=3$. Зауважте, що

\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}=\dfrac{3}{2}. \nonumber \]

Це не випадково, як викладено в наступній теоремі.

Похідна параметричних рівнянь

Розглянемо плоску криву, визначену параметричними рівняннями$x=x(t)$ і$y=y(t)$. Припустимо, що$x′(t)$ і$y′(t)$ існують, і припустимо, що$x′(t)≠0$. Тоді похідна$\dfrac{dy}{dx}$ дається

\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}=\dfrac{y′(t)}{x′(t)}. \label{paraD} \]

Доказ

Цю теорему можна довести за допомогою правила ланцюга. Зокрема, припустимо, що параметр$t$ можна усунути, даючи диференційовану функцію$y=F(x)$. Тоді$y(t)=F(x(t)).$ диференціація обох сторін цього рівняння за допомогою правила ланцюга дає

\[y′(t)=F′\big(x(t)\big)x′(t), \nonumber \]

тому

\[F′\big(x(t)\big)=\dfrac{y′(t)}{x′(t)}. \nonumber \]

Але$F′\big(x(t)\big)=\dfrac{dy}{dx}$, що доводить теорема.

□

Рівняння\ ref {ParaD} може використовуватися для обчислення похідних плоских кривих, а також критичних точок. Нагадаємо, що критичною точкою диференційованої функції$y=f(x)$ є будь-яка точка$x=x_0$ така, що$f′(x_0)=0$ або$f′(x_0)$ не існує. Рівняння\ ref {ParaD} дає формулу нахилу дотичної лінії до кривої, визначеної параметрично незалежно від того, чи може крива бути описана функцією$y=f(x)$ чи ні.

Приклад$\PageIndex{1}$: Finding the Derivative of a Parametric Curve

Обчисліть похідну$\dfrac{dy}{dx}$ для кожної з наступних параметрично визначених плоских кривих та знайдіть будь-які критичні точки на відповідних графіках.

$x(t)=t^2−3, \quad y(t)=2t−1, \quad\text{for }−3≤t≤4$
$x(t)=2t+1, \quad y(t)=t^3−3t+4, \quad\text{for }−2≤t≤2$
$x(t)=5\cos t, \quad y(t)=5\sin t, \quad\text{for }0≤t≤2π$

Рішення

а. щоб застосувати рівняння\ ref {ParaD}, спочатку обчислити$x′(t)$ і$y′(t)$:

$x′(t)=2t$

$y′(t)=2$.

Далі підставляємо їх у рівняння:

$\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}$

$\dfrac{dy}{dx}=\dfrac{2}{2t}$

$\dfrac{dy}{dx}=\dfrac{1}{t}$.

Ця похідна не визначена, коли$t=0$. Розрахунок$x(0)$$x(0)=(0)^2−3=−3$ і$y(0)$ дає і$y(0)=2(0)−1=−1$, який відповідає точці$(−3,−1)$ на графіку. Графік цієї кривої є параболою, що відкривається вправо, а точка$(−3,−1)$ - її вершина, як показано на малюнку.

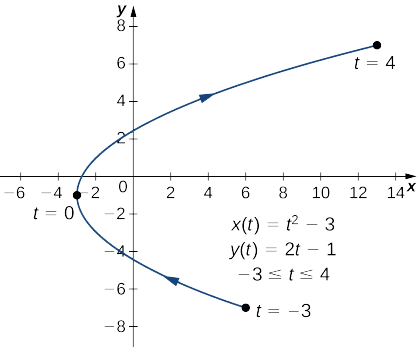
Крива лінія, що йде від (6, −7) до (−3, −1) до (13, 7) зі стрілкою, вказаною у такому порядку. Точку (6, −7) відзначають t = −3, точку (−3, −1) позначають t = 0, а точку (13, 7) позначають t = 4. На графі також записані три рівняння: x (t) = t2 − 3, y (t) = 2t − 1, і −3 ≤ t ≤ 4. — Малюнок$\PageIndex{2}$: Графік параболи, описаний параметричними рівняннями в частині а.

б Щоб застосувати рівняння\ ref {ParaD}, спочатку обчисліть$x′(t)$ і$y′(t)$:

$x′(t)=2$

$y′(t)=3t^2−3$.

Далі підставляємо їх у рівняння:

$\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}$

$\dfrac{dy}{dx}=\dfrac{3t^2−3}{2}$.

Ця похідна дорівнює нулю, коли$t=±1$. Коли у$t=−1$ нас є

$x(−1)=2(−1)+1=−1$і$y(−1)=(−1)^3−3(−1)+4=−1+3+4=6$,

яка відповідає точці$(−1,6)$ на графіку. Коли у$t=1$ нас є

$x(1)=2(1)+1=3$і$y(1)=(1)^3−3(1)+4=1−3+4=2,$

яка відповідає точці$(3,2)$ на графіку. Точка$(3,2)$ є відносним мінімумом, а точка$(−1,6)$ - відносним максимумом, як видно на наступному графіку.

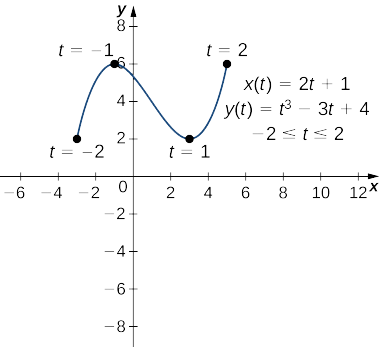
Нечітко синусоїдальна крива, що йде від (−3, 2) до (−1, 6) і (3, 2) до (5, 6). Точку (−3, 2) відзначають t = −2, точку (−1, 6) відзначають t = −1, точку (3, 2) відзначають t = 1, а точку (5, 6) відзначають t = 2. На графі також записані три рівняння: x (t) = 2t + 1, y (t) = t3 — 3t + 4, і −2 ≤ t ≤ 2. — Малюнок$\PageIndex{3}$: Графік кривої, описаної параметричними рівняннями в частині b.

c Щоб застосувати рівняння\ ref {ParaD}, спочатку обчисліть$x′(t)$ і$y′(t)$:

$x′(t)=−5\sin t$

$y′(t)=5\cos t.$

Далі підставляємо їх у рівняння:

$\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}$

$\dfrac{dy}{dx}=\dfrac{5\cos t}{−5\sin t}$

$\dfrac{dy}{dx}=−\cot t.$

Ця похідна дорівнює нулю, коли$\cos t=0$ і не визначена, коли$\sin t=0.$ Це дає$t=0,\dfrac{π}{2},π,\dfrac{3π}{2},$ і$2π$ як критичні точки для t. Підставивши кожен з них в$x(t)$ і$y(t)$, отримуємо

$t$	$x(t)$	$y(t)$
\ (t\)» style="вертикальне вирівнювання: середина; "> 0	\ (x (t)\)» style="вертикальне вирівнювання: середина; "> 5	\ (y (t)\)» style="вертикальне вирівнювання: середина; "> 0
\ (t\)» style="вертикальне вирівнювання: середина; ">$\dfrac{π}{2}$	\ (x (t)\)» style="вертикальне вирівнювання: середина; "> 0	\ (y (t)\)» style="вертикальне вирівнювання: середина; "> 5
\ (t\)» style="вертикальне вирівнювання: середина; ">$π$	\ (x (t)\)» style="вертикальне вирівнювання: середина; ">−5	\ (y (t)\)» style="вертикальне вирівнювання: середина; "> 0
\ (t\)» style="вертикальне вирівнювання: середина; ">$\dfrac{3π}{2}$	\ (x (t)\)» style="вертикальне вирівнювання: середина; "> 0	\ (y (t)\)» style="вертикальне вирівнювання: середина; ">−5
\ (t\)» style="вертикальне вирівнювання: середина; ">$2π$	\ (x (t)\)» style="вертикальне вирівнювання: середина; "> 5	\ (y (t)\)» style="вертикальне вирівнювання: середина; "> 0

Цим точкам відповідають сторони, верх і низ кола, який представлений параметричними рівняннями (рис.$\PageIndex{4}$). На лівому і правому краях кола похідна невизначена, а на верхньому і нижньому - похідна дорівнює нулю.

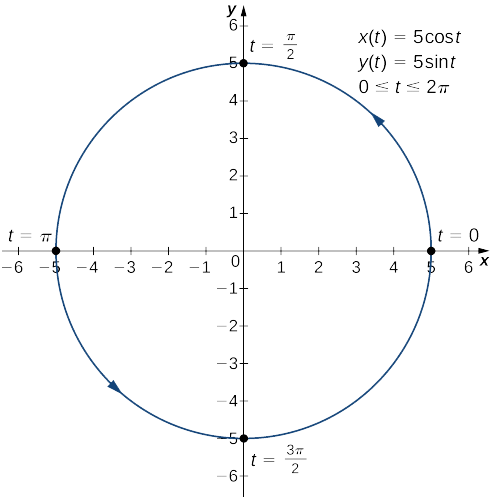
Коло з радіусом 5, центрованим у початковій точці, зображено стрілкою проти годинникової стрілки. Точку (5, 0) відзначають t = 0, точку (0, 5) відзначають t = π/2, точку (−5, 0) відзначають t = π, а точку (0, −5) відзначають t = 3π/2. На графі також записані три рівняння: x (t) = 5 cos (t), y (t) = 5 sin (t), і 0 ≤ t ≤ 2π. — Рисунок$\PageIndex{4}$: Графік кривої, описаної параметричними рівняннями в частині с.

Вправа$\PageIndex{1}$

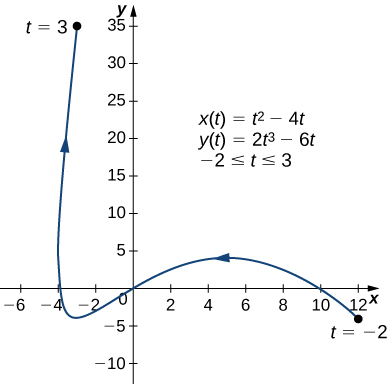
Обчислити похідну$dy/dx$ для плоской кривої, визначеної рівняннями

\[x(t)=t^2−4t, \quad y(t)=2t^3−6t, \quad\text{for }−2≤t≤3 \nonumber \]

і знайдіть будь-які критичні точки на його графіку.

Підказка: Обчислити$x′(t)$$y′(t)$ та використати рівняння\ ref {ParaD}.

Відповідь

$x′(t)=2t−4$і$y′(t)=6t^2−6$, так$\dfrac{dy}{dx}=\dfrac{6t^2−6}{2t−4}=\dfrac{3t^2−3}{t−2}$.

Цей вираз невизначений коли$t=2$ і дорівнює нулю коли$t=±1$.

$Крива, що йде від (12, −4) через початок і (−4, 0) до (−3, 36) зі стрілками у такому порядку. Точку (12, −4) позначають t = −2 і точку (−3, 36) позначають t = 3. На графі також записані три рівняння: x (t) = t2 — 4t, y (t) = 2t3 — 6t, і −2 ≤ t ≤ 3.$

Приклад$\PageIndex{2}$: Finding a Tangent Line

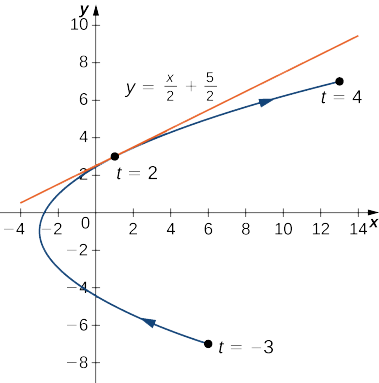
Знайти рівняння дотичної лінії до кривої, визначеної рівняннями

\[x(t)=t^2−3, \quad y(t)=2t−1, \quad\text{for }−3≤t≤4 \nonumber \]

коли$t=2$.

Рішення

Спочатку знайдіть нахил дотичної лінії за допомогою Equation\ ref {ParaD}, що означає обчислення$x′(t)$ та$y′(t)$:

$x′(t)=2t$

$y′(t)=2$.

Далі підставляємо їх у рівняння:

$\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}$

$\dfrac{dy}{dx}=\dfrac{2}{2t}$

$\dfrac{dy}{dx}=\dfrac{1}{t}$.

Коли$t=2, \dfrac{dy}{dx}=\dfrac{1}{2}$, так це нахил дотичної лінії. Розрахунок$x(2)$ і$y(2)$ дає

$x(2)=(2)^2−3=1$і$y(2)=2(2)−1=3$,

яка відповідає точці$(1,3)$ на графіку (рис.$\PageIndex{5}$). Тепер використовуйте точку-нахил форми рівняння прямої, щоб знайти рівняння дотичної лінії:

$y−y_0=m(x−x_0)$

$y−3=\dfrac{1}{2}(x−1)$

$y−3=\dfrac{1}{2}x−\dfrac{1}{2}$

$y=\dfrac{1}{2}x+\dfrac{5}{2}$.

Вправа$\PageIndex{2}$

Знайти рівняння дотичної лінії до кривої, визначеної рівняннями

$x(t)=t^2−4t, \quad y(t)=2t^3−6t, \quad\text{for }−2≤t≤6$коли$t=5$.

Підказка: Обчислити$x′(t)$$y′(t)$ та використати рівняння\ ref {ParaD}.

Відповідь: Рівняння дотичної прямої дорівнює$y=24x+100.$

Похідні другого порядку

Наша наступна мета - побачити, як взяти другу похідну функції, визначену параметрично. Друга похідна функції$y=f(x)$ визначається як похідна першої похідної; тобто

\[\dfrac{d^2y}{dx^2}=\dfrac{d}{dx}\left[\dfrac{dy}{dx}\right]. \label{eqD2} \]

Так як

\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}, \nonumber \]

ми можемо замінити з обох$y$ сторін рівняння\ ref {eQD2} на$\dfrac{dy}{dx}$. Це дає нам

\[\dfrac{d^2y}{dx^2}=\dfrac{d}{dx} \left(\dfrac{dy}{dx} \right)=\dfrac{(d/dt)(dy/dx)}{dx/dt}.\label{paraD2} \]

Якщо ми знаємо$dy/dx$ як функцію$t$, то цю формулу просто застосувати

Приклад$\PageIndex{3}$: Finding a Second Derivative

Обчислити другу похідну$d^2y/dx^2$ для плоской кривої, визначеної параметричними рівняннями$x(t)=t^2−3, \quad y(t)=2t−1, \quad\text{for }−3≤t≤4.$

Рішення

З Прикладу$\PageIndex{1}$ ми це знаємо$\dfrac{dy}{dx}=\dfrac{2}{2t}=\dfrac{1}{t}$. Використовуючи рівняння\ ref {ParaD2}, отримаємо

$\dfrac{d^2y}{dx^2}=\dfrac{(d/dt)(dy/dx)}{dx/dt}=\dfrac{(d/dt)(1/t)}{2t}=\dfrac{−t^{−2}}{2t}=−\dfrac{1}{2t^3}$.

Вправа$\PageIndex{3}$

Обчислити другу похідну$d^2y/dx^2$ для плоской кривої, визначеної рівняннями

$x(t)=t^2−4t, \quad y(t)=2t^3−6t, \quad\text{for }−2≤t≤3$

і знайдіть будь-які критичні точки на його графіку.

Підказка: Почніть з розв'язку з попередньої вправи і використовуйте Equation\ ref {ParaD2}.

Відповідь: $\dfrac{d^2y}{dx^2}=\dfrac{3t^2−12t+3}{2(t−2)^3}$. Критичні точки$(5,4),\, (−3,−4)$, і$(−4,6).$

Інтеграли за участю параметричних рівнянь

Тепер, коли ми побачили, як обчислити похідну плоської кривої, наступне питання полягає в наступному: Як знайти площу під кривою, визначеною параметрично? Згадаймо циклоїду, визначену цими параметричними рівняннями

\[ \begin{align*} x(t) &=t−\sin t \\[4pt] y(t) &=1−\cos t. \end{align*}\]

Припустимо, ми хочемо знайти площу затіненої області на наступному графіку.

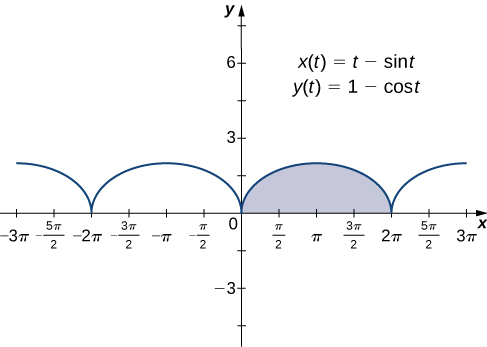
Серія напівкіл, намальованих над віссю x з перехопленнями x, кратними 2π. Підсвічується півколо між 0 і 2π. На графіку також записані два рівняння: x (t) = t — sin (t) і y (t) = 1 — cos (t). — Малюнок$\PageIndex{6}$: Графік циклоїди з$[0,2π]$ виділеною дугою.

Вивести формулу для площі під кривою, визначеної функціями

\[\begin{align*} x &=x(t) \\[4pt] y &=y(t) \end{align*}\]

де$a≤t≤b$.

Припустимо,$x(t)$ що диференційовно і починаємо з рівного поділу інтервалу$a≤t≤b$. Припустимо$t_0=a<t_1<t_2<⋯<t_n=b$ і розглянемо наступний графік.

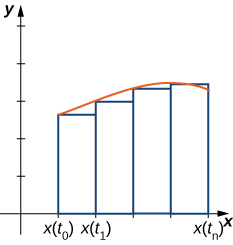
У першому квадранті проводиться крива лінія. Під ним позначені ряд прямокутників, які починаються з осі х і доходять до кривої лінії; висота прямокутника визначається розташуванням кривої лінії в крайній лівій точці прямокутника. Ці рядки відзначаються як x (t0), x (t1),..., x (tn). — Малюнок$\PageIndex{7}$: Апроксимація площі під параметрично визначеною кривою.

Використовуємо прямокутники, щоб наблизити площу під кривою. Висота типового прямокутника в цій параметризації є$y(x(\bar{t_i}))$ для деякого значення$\bar{t_i}$ в$i^\text{th}$ підінтервалі, а ширину можна обчислити як$x(t_i)−x(t_{i−1})$. Таким чином, площа$i^\text{th}$ прямокутника задається

\[A_i=y(x(\bar{t_i}))(x(t_i)−x(t_{i−1})). \nonumber \]

Тоді сума Рімана для площі дорівнює

\[A_n=\sum_{i=1}^ny(x(\bar{t_i}))(x(t_i)−x(t_{i−1})).\nonumber \]

Множення і поділ кожної області на$t_i−t_{i−1}$ дає

\[ \begin{align*} A_n &=\sum_{i=1}^ny(x(\bar{t_i})) \left(\dfrac{x(t_i)−x(t_{i−1})}{t_i−t_{i−1}}\right)(t_i−t_{i−1}) \\[4pt] &=\sum_{i=1}^ny(x(\bar{t_i})) \left(\dfrac{x(t_i)−x(t_{i−1})}{Δt}\right)Δt. \end{align*} \nonumber \]

Беручи межу у міру$n$ наближення нескінченності

\[A=\lim_{n→∞}A_n=∫^b_ay(t)x′(t)\,dt. \nonumber \]

Це призводить до наступної теореми.

Площа під параметричною кривою

Розглянемо несамопересічну площину криву, визначену параметричними рівняннями

\[x=x(t),\quad y=y(t),\quad \text{for }a≤t≤b \nonumber \]

і припустимо,$x(t)$ що диференційований. Площа під цією кривою задається

\[A=∫^b_ay(t)x′(t)\,dt.\label{ParaArea} \]

Приклад$\PageIndex{4}$: Finding the Area under a Parametric Curve

Знайти площу під кривою циклоїди, визначену рівняннями

\[x(t)=t−\sin t, \quad y(t)=1−\cos t, \quad \text{for }0≤t≤2π. \nonumber \]

Рішення

Використовуючи рівняння\ ref {ParaArea}, ми маємо

\ [\ почати {вирівнювати*} A &=^b_ay (t) x′ (t)\, dt\\ [4pt]
&=^ {2π} _0 (1−\ cos t) (1−\ cos t)\, dt\\ [4pt]
&=^ {2π} _0 (1−2\ cos t+\ cos t)\ cos ^2t)\, dt\\ [4pt]
&=^ {2π} _0\ ліворуч (1−2\ cos t+\ dfrac {1+\ cos (2t)} {2}\ праворуч)\, dt\\ [4pt]
&=^ {2π} _0\ ліворуч (\ dfrac {3} {2} −2\ cos t+ \ dfrac {\ cos (2t)} {2}\ праворуч)\, dt\\ [4pt]
&=\ dfrac {3t} {2} −2\ sin t+\ dfrac {\ sin (2t)} {4} ^ {2π} _0\\ [4pt]
&= 3π\ кінець {align*}\]

Вправа$\PageIndex{4}$

Знайти площу під кривою гіпоциклоїди, визначену рівняннями

\[x(t)=3\cos t+\cos(3t), \quad y(t)=3\sin t−\sin(3t), \quad \text{for }0≤t≤π. \nonumber \]

Підказка: Використовуйте рівняння\ ref {ParaArea} разом з тотожностями$\sin α\sin β=\dfrac{1}{2}[\cos(α−β)−\cos(α+β)]$ і$\sin^2t=\dfrac{1−\cos (2t)}{2}$.

Відповідь: $A=3π$(Зверніть увагу, що інтегральна формула насправді дає негативну відповідь. Це пов'язано з тим, що$x(t)$ є спадною функцією над інтервалом,$[0,π];$ тобто крива простежується справа наліво.)

Довжина дуги параметричної кривої

Крім знаходження площі під параметричною кривою, нам іноді потрібно знайти довжину дуги параметричної кривої. У випадку відрізка лінії довжина дуги така ж, як і відстань між кінцевими точками. Якщо частинка рухається від точки$A$ до точки$B$ вздовж кривої, то відстань, яку проходить частинка, - це довжина дуги. Щоб розробити формулу довжини дуги, почнемо з наближення відрізками ліній, як показано на наступному графіку.

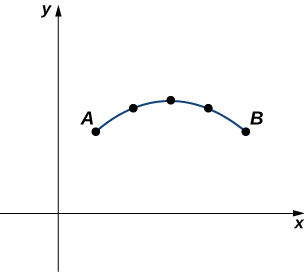
Вигнута лінія в першому квадранті з точками, позначеними для x = 1, 2, 3, 4 і 5. Ці точки мають значення приблизно 2,1, 2,7, 3, 2,7 і 2,1 відповідно. Точки для х = 1 і 5 позначаються відповідно А і В. — Малюнок$\PageIndex{7}$: Наближення кривої відрізками лінії.

З огляду на плоску криву, визначену функціями$x=x(t),\quad y=y(t),\quad \text{for }a≤t≤b$, ми почнемо з поділу інтервалу$[a,b]$ на$n$ рівні підінтервали:$t_0=a<t_1<t_2<⋯<t_n=b$. Ширина кожного підінтервалу задається значенням$Δt=(b−a)/n$. Ми можемо обчислити довжину кожного відрізка лінії:

\[d_1=\sqrt{(x(t_1)−x(t_0))^2+(y(t_1)−y(t_0))^2} \nonumber \]

\[d_2=\sqrt{(x(t_2)−x(t_1))^2+(y(t_2)−y(t_1))^2} \nonumber \]

і т.д.

Потім складіть їх. Давайте$s$ позначимо точну довжину дуги і$s_n$ позначимо наближення відрізками$n$ лінії:

\[s≈\sum_{k=1}^ns_k=\sum_{k=1}^n\sqrt{(x(t_k)−x(t_{k−1}))^2+(y(t_k)−y(t_{k−1}))^2}. \label{arc5} \]

Якщо припустити, що$x(t)$ і$y(t)$ є диференційованими функціями$t$, то застосовується теорема про середнє значення, тому в кожному підінтервалі$[t_{k−1},t_k]$ існують$\hat{t_k}$ і$\tilde{t_k}$ такі, що

\[x(t_k)−x(t_{k−1})=x′(\hat{t_k})(t_k−t_{k−1})=x′(\hat{t_k})\,Δt \nonumber \]

\[y(t_k)−y(t_{k−1})=y′(\tilde{t_k})(t_k−t_{k−1})=y′(\tilde{t_k})\,Δt. \nonumber \]

Тому рівняння\ ref {arc5} стає

\ [\ почати {вирівнювати*} s ≈\ сума_ {k=1} ^ns_k &=\ сума_ {k=1} ^n\ sqrt {(x′ (\ капелюх {t_k}) Δt) ^2+ (y′ (\ тильда {t_k}) Δt) ^2}\\ [4pt]
&=\ sum_ {k=1} ^n sqrt {(x′ (\ капелюх {t_k})) ^2 (Δt) ^2+ (y′ (\ тильда {t_k})) ^2 (Δt) ^2}\\ [4pt]
&=\ sum_ {k=1} ^n\ sqrt {(x′ (\ капелюх {t_k})) ^2+ (y′ {tilde t_k})) ^2} Δt. \ end {вирівнювати*}\]

Це сума Рімана, яка наближає довжину дуги над розділом інтервалу$[a,b]$. Якщо далі припустити, що похідні є неперервними і нехай кількість точок у розділі збільшується без обмежень, наближення наближається до точної довжини дуги. Це дає

\ [\ почати {вирівнювати*} s &=\ lim_ {n→∞}\ sum_ {k=1} ^ns_k\\ [4pt]
&=\ lim_ {n→∞}\ сума_ {k=1} ^n\ sqrt {(x′ (\ капелюх {t_k}) ^2+ (y′ (\ тильда {t_k}) ^2 Δt\\ [4pt]
&= ^b_a\ sqrt {(x′ (t)) ^2+ (y′ (t)) ^2}\, дт. \ end {вирівнювати*}\]

При прийнятті межі значення$\hat{t_k}$ і обидва$\tilde{t_k}$ містяться в одному і тому ж постійно скорочується інтервалі ширини$Δt$, тому вони повинні сходитися до одного і того ж значення.

Ми можемо узагальнити цей метод в наступній теоремі.

Довжина дуги параметричної кривої

Розглянемо плоску криву, визначену параметричними рівняннями

\[x=x(t), \quad y=y(t), \quad \text{for }t_1≤t≤t_2 \nonumber \]

і припустити, що$x(t)$ і$y(t)$ є диференційованими функціями$t$. Тоді довжина дуги цієї кривої задається

\[s=∫^{t_2}_{t_1}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt. \label{arcP} \]

На цьому етапі бічне виведення призводить до попередньої формули довжини дуги. Зокрема, припустимо, параметр можна усунути, що веде до функції$y=F(x)$. Тоді$y(t)=F(x(t))$ і правило ланцюга дає

\[y′(t)=F′\big(x(t)\big)x′(t). \nonumber \]

Підставляючи це в рівняння\ ref {ArcP} дає

\ [\ почати {align*} s &=^ {t_2} _ {t_1}\ sqrt {\ ліворуч (\ dfrac {dx} {dx}\ праворуч) ^2+\ ліворуч (F′ (x)\ dfrac {dx} {dt}\ праворуч) ^2}\, dt\\ [4pt]
&=^ {t_2} _ {t_1}}\ sqrt {\ лівий (\ dfrac {dx} {dt}\ праворуч) ^2 (1+\ ліворуч (F′ (x)\ праворуч) ^2)}\, dt\\ [4pt]
&=^ {t_2} _ {t_1} x′ (t)\ sqrt {1+\ ліворуч (\ dfrac {dx}\ праворуч) ^2}\, dt. \ end {вирівнювати*}\]

Тут ми припустили це$x′(t)>0$, що є розумним припущенням. Правило ланцюга дає$dx=x′(t)\,dt,$ і пускає,$a=x(t_1)$ і$b=x(t_2)$ ми отримуємо формулу

\[s=∫^b_a\sqrt{1+\left(\dfrac{dy}{dx}\right)^2}\,dx, \nonumber \]

яка є формулою довжини дуги, отриманої у Вступі до додатків інтеграції.

Приклад$\PageIndex{5}$: Finding the Arc Length of a Parametric Curve

Знайти довжину дуги півкола, визначену рівняннями

\[x(t)=3\cos t, \quad y(t)=3\sin t, \quad \text{for }0≤t≤π. \nonumber \]

Рішення

Значення$t=0$ для$t=π$ трасування синьої кривої на малюнку$\PageIndex{8}$. Щоб визначити його довжину, скористайтеся Equation\ ref {ArcP}:

\ [\ почати {align*} s &=\ int^ {t_2} _ {t_1}\ sqrt {\ лівий (\ dfrac {dx} {dx} {dt}\ праворуч) ^2+\ ліворуч (\ dfrac {dy} {dt}\ праворуч) ^2}\, dt\\ [4pt]
&= ^π_0\ sqrt {−3\ sin t) ^2+ (3\ cos t) ^2}\, дт\\ [4пт]
&=^π_0\ sqrt {9\ sin^2t+9\ cos^2t}\, дт\\ [4пт]
&= ^π_0\ sqrt {9 (\ sin^2t+\ cos^2t)}\ dt\\ [4pt]
&=^π_03\, dt = 3t\ big|^π_0\\ [4pt]
&=3π\ текст {одиниці}. \ end {вирівнювати*}\]

Зверніть увагу, що формула довжини дуги півкола дорівнює$πr$ і радіус цього кола дорівнює$3$. Це чудовий приклад використання числення для отримання відомої формули геометричної величини.

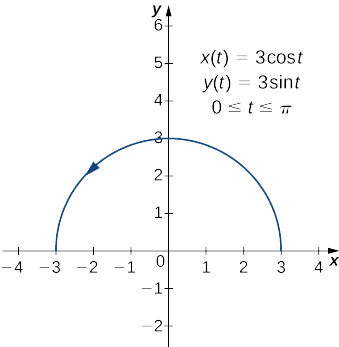
Намальовується півколо радіусом 3. Є стрілка, спрямована проти годинникової стрілки. На графі також записані три рівняння: x (t) = 3 cos (t), y (t) = 3 sin (t), і 0 ≤ t ≤ π. — Малюнок$\PageIndex{8}$: Довжина дуги півкола дорівнює його радіусу раз$π$.

Вправа$\PageIndex{5}$

Знайти довжину дуги кривої, визначеної рівняннями

\[x(t)=3t^2, \quad y(t)=2t^3, \quad \text{for }1≤t≤3. \nonumber \]

Підказка: Використовуйте рівняння\ ref {ArcP}.

Відповідь: $s=2(10^{3/2}−2^{3/2})≈57.589$одиниць

Тепер ми повернемося до проблеми, поставленої на початку розділу про бейсбол, залишаючи руку глечика. Ігнорування ефекту опору повітря (якщо це не крива куля!) , м'яч подорожує параболічним шляхом. Припускаючи, що рука глечика знаходиться біля початку, а м'яч рухається зліва направо у напрямку позитивної$x$ осі, параметричні рівняння для цієї кривої можна записати як

\[x(t)=140t, \quad y(t)=−16t^2+2t \nonumber \]

де$t$ позначає час. Спочатку обчислюємо відстань, яку проїжджає куля, як функція часу. Ця відстань представлена довжиною дуги. Ми можемо трохи змінити формулу довжини дуги. Спочатку перепишіть функції$x(t)$ і$y(t)$ використовуючи v як незалежну змінну, щоб виключити будь-яку плутанину з параметром$t$:

\[x(v)=140v, \quad y(v)=−16v^2+2v. \nonumber \]

Потім пишемо формулу довжини дуги наступним чином:

\ [\ почати {вирівнювати*} s (t) &=^t_0\ sqrt {(\ dfrac {dx} {dv}) ^2+ (\ dfrac {dy} {dv}) ^2}\, dv\\ [4pt]
&=^t_0\ sqrt {140^2+ (−32v+2) ^2}\ dv\ кінець {вирівнювати*}\]

Змінна$v$ діє як фіктивна змінна, яка зникає після інтеграції, залишаючи довжину дуги як функцію часу$t$. Для інтеграції цього виразу ми можемо використовувати формулу з Додатка А,

\[∫\sqrt{a^2+u^2}\,du=\dfrac{u}{2}\sqrt{a^2+u^2}+\dfrac{a^2}{2}\ln ∣u+\sqrt{a^2+u^2}∣+C. \nonumber \]

Ми встановлюємо$a=140$ і$u=−32v+2.$ Це дає$du=−32\,dv,$ так$dv=−\dfrac{1}{32}\,du.$ Тому

\ [\ почати {вирівнювати*}\ sqrt {140^2+ (−32v+2) ^2}\, dv &=−\ dfrac {1} {32}\ sqrt {a^2+u^2}\, ду\\ [4pt]
&=−\ dfrac {1} {32}\ ліворуч [\ dfrac {(−32v+2} {2}\ sqrt {140^2+ (−32v+2) ^2} +\ dfrac {140^2} {2}\ ln (−32v+2) +\ sqrt {140^2+ (−32v+2) ^2} |+C\ праворуч]\ кінець {вирівнювати*}\]

\ [\ почати {вирівнювати*} s (t) &=-\ dfrac {1} {32}\ ліворуч [\ dfrac {(-32t+2)} {2}\ sqrt {140^2+ (-32t+2) ^2} +\ dfrac {140^2} {2}\ ln\ ліворуч | (-32t+2) +\ sqrt {140^2+ (-32t+2) ^2}\ праворуч |\ праворуч] +\ dfrac {1} {32}\ ліворуч [\ sqrt {140^2^2} +\ dfrac {140^2} {2}\ ln\ ліворуч |2+\ sqrt {140^2^2}\ праворуч |\\ праворуч]\\ [4pt]
&=\ ліворуч (\ dfrac {t} {2} -\ dfrac {1} {32}\ праворуч)\ sqrt {1024t^2-128t+19604} -\ dfrac {1225} {4}\ на\ ліворуч | (-32t+2) +\ sqrt {1024t^2-128t+19604}\ праворуч |+\ dfrac {\ sqrt {19604}} {32} +\ dfrac {128t+12604} 25} {4}\ ln (2+\ sqrt {19604})\ end {вирівнювати*}. \ номер\]

Ця функція представляє відстань, пройдену м'ячем, як функцію часу. Для обчислення швидкості візьміть похідну від цієї функції щодо$t$. Хоча це може здатися складним завданням, можна отримати відповідь безпосередньо з Фундаментальної теореми обчислення:

\[\dfrac{d}{dx}∫^x_af(u)\,du=f(x). \nonumber \]

Тому

\ [\ почати {вирівнювати*} s′ (t) &=\ dfrac {d} {dt}\ Великий [s (t)\ Великий]\\ [4pt]
&=\ dfrac {d} {dt}\ ліворуч [^t_0\ sqrt {140^2+ (−32v+2) ^2}\, дв\ праворуч]\\ [4pt]
&= sqrt {140^2+ (−32t+2) ^2}\\ [4pt]
&=\ sqrt {1024t^2−128t+19604}\\ [4pt]
&= 2\ sqrt {256t^2−32t+4901}. \ end {вирівнювати*}\ nonumber\]

Третина секунди після того, як м'яч покине руку глечика, відстань, яку він проходить, дорівнює

\ [\ begin {align*} s\ лівий (\ frac {1} {3}\ праворуч) &=\ ліворуч (\ frac {1/3} {2} −\ frac {1} {32}\ праворуч)\ sqrt {1024\ ліворуч (\ frac {1}\ праворуч) ^2−128\ ліворуч (\ frac {1} {3}\ праворуч) ^2−128\ ліворуч (\ frac {1} {3}\ праворуч) +19604}\\
&−\ frac {1225} {4}\ ln\ Bigg|\ ліворуч (−32\ ліворуч (\ frac {1} {3}\ праворуч) +2\ вправо) +\ sqrt {1024\ ліворуч (\ frac {1}\ праворуч) ^−2128\ ліворуч (\ frac {1} {3}\ праворуч) +19604}\ Біг|\\
&+\ frac {\ sqrt {19604}} {32} +\ frac {1225} {4}\ ln (2+\ sqrt {19604})\\ [4pt]
&≈46.69\ текст {фути}. \ end {вирівнювати*}\]

Це значення становить трохи більше трьох чвертей шляху до домашньої плити. Швидкість м'яча дорівнює

$s′\left(\frac{1}{3}\right)=2\sqrt{256\left(\frac{1}{3}\right)^2−32\left(\frac{1}{3}\right)+4901}≈140.27$фут/с.

Ця швидкість перекладається приблизно на$95$ годину - фастбол великої ліги.

Площа поверхні, породжена параметричною кривою

Згадаймо проблему знаходження площі поверхні об'єму обертання. У розділі «Довжина кривої» та «Площа поверхні» ми вивели формулу для знаходження площі поверхні об'єму, що генерується функцією$y=f(x)$ від$x=a$ до$x=b,$ обертається навколо$x$ осі -:

\[S=2π∫^b_af(x)\sqrt{1+(f′(x))^2}\,dx. \nonumber \]

Зараз ми розглянемо обсяг обертання, породжений обертанням параметрично визначеної кривої$x=x(t), \quad y=y(t), \quad \text{for }a≤t≤b$ навколо$x$ осі -як показано на малюнку$\PageIndex{9}$.

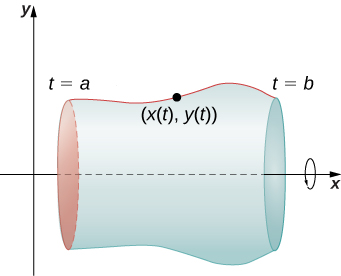
У першому квадранті малюється крива з позначеними кінцевими точками t = a і t = b, на цій кривій розмічена точка (x (t), y (t)). Існує коло зі стрілкою, намальованою навколо осі x, яка, здається, вказує на обертання навколо осі x, і є форма, яка супроводжує цю криву, яка, здається, є тим, що ви отримаєте, якщо ви повернете криву навколо осі x. — Рисунок$\PageIndex{9}$: Поверхня обертання, породжена параметрично визначеною кривою.

Аналогічна формула для параметрично визначеної кривої

\[S=2π∫^b_ay(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt \label{ParSurface} \]

за умови, що не$y(t)$ є негативним на$[a,b]$.

Приклад$\PageIndex{6}$: Finding Surface Area

Знайдіть площу поверхні сфери радіуса,$r$ зосередженої на початку координат.

Рішення

Починаємо з кривої, визначеної рівняннями

\[x(t)=r\cos t, \quad y(t)=r\sin t, \quad \text{for }0≤t≤π. \nonumber \]

Це створює верхнє півколо радіуса з$r$ центром у початковій точці, як показано на наступному графіку.

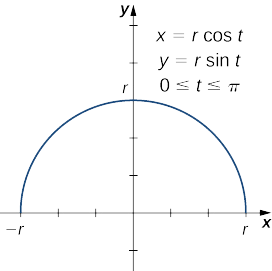
На графіку також записані три рівняння: x (t) = r cos (t), y (t) = r cos (t), y (t) = r sin (t), і 0 ≤ t ≤ π. — Малюнок$\PageIndex{10}$: Півколо, породжене параметричними рівняннями.

Коли ця крива обертається навколо$x$ -осі, вона генерує сферу радіуса$r$. Для обчислення площі поверхні сфери використовуємо Equation\ ref {ParSurface}:

\ [\ почати {вирівнювати*} S &= 2π^b_ay (t)\ sqrt {(x′ (t)) ^2+ (y′ (t)) ^2}\, dt\\ [4pt]
&=2π^π_0r\ sin t\ sqrt {(−r\ sin t) ^2+ (r\ cos t) ^2}\ dt\ [4pt]
&= 2π^π_0r\ син т\ sqrt {r^2\ sin^2t+r^2\ cos^2t}\, dt\\ [4pt]
&=2π^π_0r\ sin t\ sqrt {r^2 (\ sin^2t+\ cos^2t)}\, дт\\ [4пт]
&=2π^π_0r^2\ sin t\, dt\\ [4pt]
&= 2πr^2\ ліворуч (−\ cos t\ big|^π_0\ праворуч)\\ [4pt]
&= 2πr^2 (\ cos π+\ cos 0)\\ [4pt]
&= 4πr^2\ текст {одиниці} ^2. \ end {вирівнювати*}\ nonumber\]

Це, по суті, формула для площі поверхні кулі.

Вправа$\PageIndex{6}$

Знайти площу поверхні, що генерується, коли плоска крива визначена рівняннями

\[x(t)=t^3, \quad y(t)=t^2, \quad \text{for }0≤t≤1 \nonumber \]

обертається навколо$x$ -осі.

Підказка: Використовуйте рівняння\ ref {ParSurface}. При оцінці інтеграла використовують$u$ -підстановку.

Відповідь: $A=\dfrac{π(494\sqrt{13}+128)}{1215} \text{ units}^2$

Ключові концепції

Похідна параметрично визначеної кривої$x=x(t)$ і$y=y(t)$ може бути розрахована за формулою$\dfrac{dy}{dx}=\dfrac{y′(t)}{x′(t)}$. Використовуючи похідну, ми можемо знайти рівняння дотичної прямої до параметричної кривої.
Площа між параметричною кривою і$x$ -віссю може бути визначена за формулою$\displaystyle A=∫^{t_2}_{t_1}y(t)x′(t)\,dt.$
Довжину дуги параметричної кривої можна обчислити за формулою\[s=∫^{t_2}_{t_1}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt. \nonumber \]
Площа поверхні об'єму обертання, що обертається навколо$x$ -осі, задається\[S=2π∫^b_ay(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt. \nonumber \]
Якщо крива обертається навколо$y$ -осі, то формула\[S=2π∫^b_a x(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt. \nonumber \]

Ключові рівняння

Похідна параметричних рівнянь

\[\dfrac{dy}{dx}=\dfrac{dy/dt}{dx/dt}=\dfrac{y′(t)}{x′(t)} \nonumber \]

Похідна параметричних рівнянь другого порядку

\[\dfrac{d^2y}{dx^2}=\dfrac{d}{dx}\left(\dfrac{dy}{dx}\right)=\dfrac{(d/dt)(dy/dx)}{dx/dt} \nonumber \]

Площа під параметричною кривою

\[A=∫^b_ay(t)x′(t)\,dt \nonumber \]

Довжина дуги параметричної кривої

\[s=∫^{t_2}_{t_1}\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}\,dt \nonumber \]

Площа поверхні, породжена параметричною кривою

\[S=2π∫^b_ay(t)\sqrt{(x′(t))^2+(y′(t))^2}\,dt \nonumber \]

Похідна параметричних рівнянь

Доказ

Приклад\(\PageIndex{1}\): Finding the Derivative of a Parametric Curve

Вправа\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\): Finding a Tangent Line

Вправа\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\): Finding a Second Derivative

Вправа\(\PageIndex{3}\)

Площа під параметричною кривою

Приклад\(\PageIndex{4}\): Finding the Area under a Parametric Curve

Вправа\(\PageIndex{4}\)

Довжина дуги параметричної кривої

Приклад\(\PageIndex{5}\): Finding the Arc Length of a Parametric Curve

Вправа\(\PageIndex{5}\)

Приклад\(\PageIndex{6}\): Finding Surface Area

Вправа\(\PageIndex{6}\)