9.5: Чергування серії
- Page ID
- 62204
- Використовуйте тест чергування серії, щоб перевірити змінний ряд на збіжність.
- Оцініть суму чергуються ряду.
- Поясніть значення абсолютної збіжності і умовної конвергенції.
Поки що в цьому розділі ми в першу чергу обговорювали серії з позитивними термінами. У цьому розділі ми вводимо чергуються ряди - ті ряди, чиї терміни чергуються за знаком. Ми покажемо в наступному розділі, що ці серії часто виникають при вивченні силових рядів. Визначивши чергуються ряди, ми вводимо тест чергуються рядів, щоб визначити, чи сходиться такий ряд.
Тест на чергування серії
Ряд, чиї члени чергуються між додатними і негативними значеннями, є чергуються рядами. Наприклад, серіал
\[\sum_{n=1}^∞ \left(−\dfrac{1}{2} \right)^n=−\dfrac{1}{2}+\dfrac{1}{4}−\dfrac{1}{8}+\dfrac{1}{16}− \ldots \label{eq1} \]
і
\[\sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\ldots \label{eq2} \]
обидва чергуються ряди.
Будь-який ряд, чиї члени чергуються між додатними і негативними значеннями, називається чергуються рядами. Чергуючий ряд можна записати у вигляді
\[\sum_{n=1}^∞(−1)^{n+1}b_n=b_1−b_2+b_3−b_4+ \ldots \label{eq3} \]
або
\[\sum_{n−1}^∞(−1)^nb_n=−b_1+b_2−b_3+b_4−\ldots \label{eq4} \]
Де\( b_n≥0\) для всіх натуральних чисел\(n\).
Серія (1), показана в Equation\ ref {eq1}, є геометричним рядом. Так як\( |r|=|−1/2|<1,\) ряд сходиться. Серія (2), показана в Equation\ ref {eq2}, називається змінним гармонічним рядом. Ми покажемо, що в той час як гармонійний ряд розходиться, змінний гармонічний ряд сходиться. Щоб довести це, розглянемо послідовність часткових сум\( \{S_k\}\) (рис. 1).
Розглянемо непарні терміни\( S_{2k+1}\) для\( k≥0\). Так як\( 1/(2k+1)<1/2k,\)
\[S_{2k+1}=S_{2k−1}−\dfrac{1}{2k}+\dfrac{1}{2k+1}<S_{2k−1}. \nonumber \]
Тому\( \{S_{2k+1}\}\) відбувається спадна послідовність. Крім того,
\[S_{2k+1}=\left(1−\dfrac{1}{2}\right)+\left(\dfrac{1}{3}−\dfrac{1}{4}\right)+ \ldots + \left(\dfrac{1}{2k−1}−\dfrac{1}{2k}\right)+\dfrac{1}{2k+1}>0. \nonumber \]
Тому\( \{S_{2k+1}\}\) обмежується нижче. Оскільки\( \{S_{2k+1}\}\) є спадною послідовністю, яка обмежена нижче, теоремою монотонної збіжності\( \{S_{2k+1}\}\) сходиться. Аналогічно, парні терміни\( \{S_{2k}\}\) утворюють зростаючу послідовність, яка обмежена вище, оскільки
\[S_{2k}=S_{2k−2}+\dfrac{1}{2k−1}−\dfrac{1}{2k}>S_{2k−2} \nonumber \]
і
\[S_{2k}=1+ \left(−\dfrac{1}{2}+\dfrac{1}{3}\right)+\ldots + \left(−\dfrac{1}{2k−2}+\dfrac{1}{2k−1}\right)−\dfrac{1}{2k}<1. \nonumber \]
Тому за теоремою монотонної збіжності послідовність\( \{S_{2k}\}\) також сходиться. Так як
\[S_{2k+1}=S_{2k}+\dfrac{1}{2k+1}, \nonumber \]
ми знаємо, що
\[\lim_{k→∞}S_{2k+1}=\lim_{k→∞}S_{2k}+\lim_{k→∞}\dfrac{1}{2k+1}. \nonumber \]
Допускаючи\(\displaystyle S=\lim_{k→∞}S_{2k+1}\) і використовуючи той факт, що\( 1/(2k+1)→0,\) ми робимо висновок про це\(\displaystyle \lim_{k→∞}S_{2k}=S\). Оскільки непарні і парні члени в послідовності часткових сум сходяться до однієї межі\( S\), то можна показати, що послідовність часткових сум сходиться до\( S\), і тому змінний гармонічний ряд сходиться до\( S\).
Також можна показати, що\( S=\ln 2,\) і ми можемо написати
\[\sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+a\ldots=\ln (2). \nonumber \]
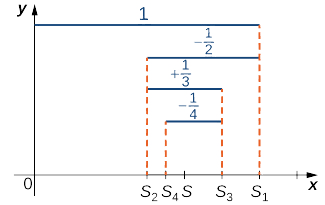
□
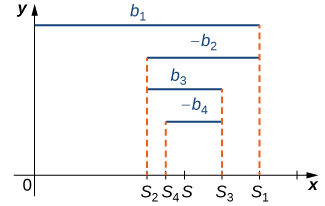
Більш загально, будь-який змінний ряд форми (3) (Equation\ ref {eq3}) або (4) (Рівняння\ ref {eq4}) сходиться до тих пір, поки\( b_1≥b_2≥b_3≥⋯\) і\( b_n→0\) (Рисунок 2). Доказ схожий на доказ для змінного гармонійного ряду.
Чергуються ряди форми
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]або\[\sum_{n=1}^∞(−1)^nb_n \nonumber \]
сходиться, якщо
- \( 0≤b_{n+1}≤b_n\)для всіх\( n≥1\) і
- \(\displaystyle \lim_{n→∞}b_n=0.\)
Це відоме як тест чергування серії.
Ми зауважимо, що ця теорема вірна більш загалом, поки існує якесь ціле число,\( N\) таке, що\( 0≤b_{n+1}≤b_n\) для всіх\( n≥N.\)
Для кожного з наступних чергуються рядів визначте, сходиться чи розходиться ряд.
- \(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{n^2}\)
- \(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{n+1}\)
Рішення
а. з тих пір\( \dfrac{1}{(n+1)^2}<\dfrac{1}{n^2}\) і\( \dfrac{1}{n^2}→0,\) ряд сходиться.
b Оскільки\( n/(n+1)↛0\) як\( n→∞\), ми не можемо застосувати тест чергування серії. Замість цього ми використовуємо n-й термін тест на дивергенцію. Так як\(\displaystyle \lim_{n→∞}\dfrac{n}{n+1}=1≠0,\) ряд розходиться.
Визначте,\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{2^n}\) сходиться чи розходиться ряд.
- Підказка
-
Чи\( \left\{\frac{n}{2^n}\right\}\) зменшується? Що таке\(\displaystyle \lim_{n→∞}\frac{n}{2^n}\)?
- Відповідь
-
Серія сходиться.
Залишок чергуються рядів
Важко явно обчислити суму більшості змінних рядів, тому зазвичай сума наближається за допомогою часткової суми. При цьому нас цікавить кількість похибки в нашому наближенні. Розглянемо чергуються ряди
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]
задовольняючи гіпотези тесту чергуються рядів. \( S\)Дозволяти позначити суму цього ряду і\( {S_k}\) бути відповідною послідовністю часткових сум. З рисунка ми бачимо\( \PageIndex{2}\), що для будь-якого цілого\( N≥1\), залишок\( R_N\) задовольняє
\[|R_N|=|S−S_N|≤|S_{N+1}−S_N|=b_{n+1}. \nonumber \]
Розглянемо чергуються ряди форми
\[\sum_{n=1}^∞(−1)^{n+1}b_n \nonumber \]або\[\sum_{n=1}^∞(−1)^nb_n \nonumber \]
що задовольняє гіпотези тесту чергуються рядів. Нехай\( S\) позначають суму ряду і\( S_N\) позначають\(N^{\text{th}}\) часткову суму. Для будь-якого цілого числа\( N≥1\) залишок\( R_N=S−S_N\) задовольняє
\[|R_N|≤b_{N+1}. \nonumber \]
Іншими словами, якщо застосовуються умови тесту змінного ряду, то похибка в наближенні нескінченного ряду\(N^{\text{th}}\) частковою сумою\( S_N\) становить за величиною не більше розміру наступного члена\( b_{N+1}\).
Розглянемо чергуються ряди
\[ \sum_{n=1}^∞\dfrac{(−1)^{n+1}}{n^2}. \nonumber \]
Використовуйте оцінку залишку, щоб визначити межу на похибці,\( R_{10}\) якщо ми наближаємо суму ряду на часткову суму\( S_{10}\).
Рішення
З теореми, викладеної вище,\[ |R_{10}|≤b_{11}=\dfrac{1}{11^2}≈0.008265. \nonumber \]
Знайти прив'язку для\( R_{20}\) при наближенні\(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{n}\) по\( S_{20}\).
- Підказка
-
\( |R_{20}|≤b_{21}\)
- Відповідь
-
\( 0.04762\)
Абсолютна і умовна збіжність
Розглянемо серію\(\displaystyle \sum_{n=1}^∞a_n\) і пов'язані з ними серії\(\displaystyle \sum_{n=1}^∞|a_n|\). Тут ми обговорюємо можливості зв'язку між конвергенцією цих двох рядів. Для прикладу розглянемо чергуються гармонійні ряди\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n}\). Ряд, чиї члени є абсолютним значенням цих членів, є гармонійним рядом,\(\displaystyle \sum_{n=1}^∞\left|\frac{(−1)^{n+1}}{n}\right|=\sum_{n=1}^∞\frac{1}{n}.\) оскільки змінний гармонічний ряд сходиться, але гармонічний ряд розходиться, ми говоримо, що змінний гармонічний ряд проявляє умовну збіжність.
Для порівняння розглянемо ряд Серія\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n^2}.\), чиї члени є абсолютними значеннями членів цього ряду, є серією\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}.\) Оскільки обидва ці ряди сходяться, ми говоримо, що ряд\(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n+1}}{n^2}\) демонструє абсолютну конвергенцію.
Ряд\(\displaystyle \sum^∞_{n=1}a_n\) демонструє абсолютну конвергенцію, якщо\(\displaystyle \sum^∞_{n=1}|a_n|\) сходиться. Ряд\(\displaystyle \sum^∞_{n=1}a_n\) демонструє умовну конвергенцію, якщо\(\displaystyle \sum^∞_{n=1}a_n\)\(\displaystyle \sum^∞_{n=1}|a_n|\) сходиться, але розходиться.
Як показує змінний гармонічний ряд, ряд\(\displaystyle \sum^∞_{n=1}a_n\) може сходитися, але\(\displaystyle \sum^∞_{n=1}|a_n|\) може розходитися. У наступній теоремі, однак, ми покажемо, що якщо\(\displaystyle \sum^∞_{n=1}|a_n|\) сходиться, то\(\displaystyle \sum^∞_{n=1}a_n\) сходиться.
Якщо\(\displaystyle \sum^∞_{n=1}|a_n|\) сходиться, то\(\displaystyle \sum^∞_{n=1}a_n\) сходиться.
Припустимо, що\(\displaystyle \sum_{n=1}^∞|a_n|\) сходиться. Ми показуємо це, використовуючи той факт, що\( a_n=|a_n\) або\( a_n=−|a_n|\) і, отже,\( |a_n|+a_n=2|a_n|\) або\( |a_n|+a_n=0\). Тому,\( 0≤|a_n|+a_n≤2|a_n|\). Отже, за допомогою тесту порівняння, оскільки\( 2\sum^∞_{n=1}|a_n|\) сходиться, ряд
\[\sum_{n=1}^∞(|a_n|+a_n) \nonumber \]
сходиться. Використовуючи алгебраїчні властивості для збіжних рядів, ми робимо висновок, що
\[\sum_{n=1}^∞a_n=\sum_{n=1}^∞(|a_n|+a_n)−\sum_{n=1}^∞|a_n| \nonumber \]
сходиться.
□
Для кожного з наступних рядів визначте, чи збігається ряд абсолютно, сходиться умовно або розходиться.
- \(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{3n+1}\)
- \(\displaystyle \sum^∞_{n=1}\frac{\cos(n)}{n^2}\)
Рішення
а. ми бачимо, що
\(\displaystyle \sum_{n=1}^∞\left|\dfrac{(−1)^{n+1}}{3n+1}\right|=\sum_{n=1}^∞\dfrac{1}{3n+1}\)
розходиться за допомогою тесту граничного порівняння з гармонічним рядом. Фактично,
\(\displaystyle \lim_{n→∞}\dfrac{1/(3n+1)}{1/n}=\dfrac{1}{3}\).
Тому ряд не сходиться абсолютно. Однак, так як
\( \dfrac{1}{3(n+1)+1}<\dfrac{1}{3n+1}\)і\( \dfrac{1}{3n+1}→0\),
серія сходиться. Можна зробити висновок, що\(\displaystyle \sum^∞_{n=1}\frac{(−1)^{n+1}}{3n+1}\) сходиться умовно.
b. зазначивши, що\( |\cos n|≤1,\) для визначення того, чи збігається ряд абсолютно, порівняйте
\(\displaystyle \sum_{n=1}^∞\left|\dfrac{\cos n}{n^2}\right|\)
з серією\(\displaystyle \sum^∞_{n=1}\frac{1}{n^2}\). Так як\(\displaystyle \sum^∞_{n=1}\frac{1}{n^2}\) сходиться, за тестом порівняння,\(\displaystyle \sum^∞_{n=1}\left|\frac{\cos n}{n^2}\right|\) сходиться, а тому\(\displaystyle \sum^∞_{n=1}\frac{\cos n}{n^2}\) сходиться абсолютно.
Визначте, чи\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{n}{2n^3+1}\) збігається ряд абсолютно, сходиться умовно або розходиться.
- Підказка
-
Спочатку перевірте абсолютну конвергенцію.
- Відповідь
-
Серія сходиться абсолютно.
Щоб побачити різницю між абсолютною та умовною збіжністю, подивіться, що відбувається, коли ми переставляємо члени змінного гармонійного ряду\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}\frac{1}{n}\). Ми показуємо, що можемо переставити терміни так, щоб нова серія розходилася. Звичайно, якщо ми переставляємо терміни кінцевої суми, сума не змінюється. Однак, коли ми працюємо з нескінченною сумою, можуть статися цікаві речі.
Почніть з додавання достатньої кількості позитивних членів, щоб отримати суму, яка більше, ніж деяке дійсне число\( M=10\) Наприклад, нехай\( M=10,\) і знайти ціле число\( k\) таке, що
\[1+\dfrac{1}{3}+\dfrac{1}{5}+⋯+\dfrac{1}{2k−1}>10 \nonumber \]
(Ми можемо це зробити, тому що серія\(\displaystyle \sum^∞_{n=1}\frac{1}{2n−1}\) розходиться до нескінченності.) Потім відніміть\( 1/2\). Потім додайте більше позитивних членів, поки сума не досягне 100. Тобто знайти інше ціле число\( j>k\) таке, що
\[(1+\dfrac{1}{3}+⋯+\dfrac{1}{2k−1}−\dfrac{1}{2}+\dfrac{1}{2k+1}+ \ldots +\dfrac{1}{2j+1}>100. \nonumber \]
Потім відніміть\( 1/4.\) Продовжуючи таким чином, ми знайшли спосіб перестановки членів в змінному гармонічному ряді так, щоб послідовність часткових сум для переставленого ряду була необмеженою і, отже, розходилася.
Терміни в змінному гармонічному ряді також можуть бути переставлені так, щоб новий ряд сходився до іншого значення. У прикладі ми покажемо, як переставити терміни, щоб створити новий ряд, який сходиться до\( 3\ln(2)/2\). Ми вказуємо, що змінний гармонічний ряд може бути перебудований, щоб створити ряд, який сходиться до будь-якого дійсного числа\( r\); однак доказ цього факту виходить за рамки цього тексту.
Взагалі, будь-який ряд,\(\displaystyle \sum^∞_{n=1}a_n\) який сходиться умовно, можна переставити так, щоб новий ряд розходився або сходився в інше дійсне число. Серія, яка сходиться абсолютно не має цієї властивості. Для будь-якого ряду,\(\displaystyle \sum^∞_{n=1}a_n\) який сходиться абсолютно, значення\(\displaystyle \sum^∞_{n=1}a_n\) однакове для будь-якої перестановки термінів. Цей результат відомий як Теорема про перестановку Рімана, яка виходить за рамки цієї книги.
Використовуйте той факт, що
\[ 1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\dfrac{1}{5}−⋯=\ln 2 \nonumber \]
переставити члени в змінному гармонічному ряді, так що сума переставленого ряду дорівнює\( 3\ln (2)/2.\)
Рішення
Нехай
\[ \sum_{n=1}^∞a_n=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\dfrac{1}{5}−\dfrac{1}{6}+\dfrac{1}{7}−\dfrac{1}{8}+⋯. \nonumber \]
Оскільки\(\displaystyle \sum_{n=1}^∞a_n=\ln (2)\), за алгебраїчними властивостями збіжних рядів,
\[ \sum_{n=1}^∞\dfrac{1}{2}a_n=\dfrac{1}{2}−\dfrac{1}{4}+\dfrac{1}{6}−\dfrac{1}{8}+⋯=\dfrac{1}{2}\sum_{n=1}^∞a_n=\dfrac{\ln 2}{2}. \nonumber \]
Тепер представляємо серію\(\displaystyle \sum_{n=1}^∞b_n\) таку, що для всіх\( n≥1, b_{2n−1}=0\) і\( b_{2n}=a_n/2.\) тоді
\[ \sum_{n=1}^∞b_n=0+\dfrac{1}{2}+0−\dfrac{1}{4}+0+\dfrac{1}{6}+0−\dfrac{1}{8}+⋯=\dfrac{\ln 2}{2}. \nonumber \]
Потім за допомогою алгебраїчних граничних властивостей збіжних рядів, так як\(\displaystyle \sum_{n=1}^∞a_n\) і\(\displaystyle \sum_{n=1}^∞b_n\) сходяться, ряд\(\displaystyle \sum_{n=1}^∞(a_n+b_n)\) сходиться і
\[ \sum_{n=1}^∞(a_n+b_n)=\sum_{n=1}^∞a_n+\sum_{n=1}^∞b_n=\ln 2+\dfrac{\ln 2}{2}=\dfrac{3\ln 2}{2}. \nonumber \]
Тепер додаємо відповідні терміни,\( a_n\) і\( b_n\), ми бачимо, що
\[ \sum_{n=1}^∞(a_n+b_n)=(1+0)+\left(−\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(\dfrac{1}{3}+0\right)+\left(−\dfrac{1}{4}−14\right)+\left(\dfrac{1}{5}+0\right)+\left(−\dfrac{1}{6}+\dfrac{1}{6}\right)+\left(\dfrac{1}{7}+0\right)+\left(\dfrac{1}{8}−\dfrac{1}{8}\right)+⋯=1+\dfrac{1}{3}−\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}−\dfrac{1}{4}+⋯. \nonumber \]
Ми помічаємо, що ряд з правого боку знака рівності є перестановкою змінного гармонійного ряду. Оскільки\(\displaystyle \sum_{n=1}^∞(a_n+b_n)=3\ln (2)/2,\) ми робимо висновок, що
\[ 1+\dfrac{1}{3}−\dfrac{1}{2}+\dfrac{1}{5}+\dfrac{1}{7}−\dfrac{1}{4}+⋯=\dfrac{3\ln (2)}{2}. \nonumber \]
Тому ми знайшли перестановку змінного гармонійного ряду, що має потрібну властивість.
Ключові концепції
- Для чергуються\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n,\) рядів якщо\( b_{k+1}≤b_k\) для всіх\( k\) і\( b_k→0\) як\( k→∞,\) чергуються ряди сходяться.
- Якщо\(\displaystyle \sum^∞_{n=1}|a_n|\) сходиться, то\(\displaystyle \sum^∞_{n=1}a_n\) сходиться.
Ключові рівняння
- чергування серій
\(\displaystyle \sum_{n=1}^∞(−1)^{n+1}b_n=b_1−b_2+b_3−b_4+⋯\)або
\(\displaystyle \sum_{n=1}^∞(−1)^nb_n=−b_1+b_2−b_3+b_4−⋯\)
Глосарій
- абсолютна конвергенція
- якщо серія\(\displaystyle \sum^∞_{n=1}|a_n|\) сходиться, то серія,\(\displaystyle \sum^∞_{n=1}a_n\) як кажуть, сходиться абсолютно
- чергування серій
- серія форми\(\displaystyle \sum^∞_{n=1}(−1)^{n+1}b_n\) або\(\displaystyle \sum^∞_{n=1}(−1)^nb_n\), де\( b_n≥0\), називається чергуються ряд
- чергування серії випробувань
- для чергуються рядів будь-якої форми, якщо\( b_{n+1}≤b_n\) для всіх цілих чисел\( n≥1\) і\( b_n→0\), то змінний ряд сходиться
- умовна конвергенція
- якщо ряд\(\displaystyle \sum^∞_{n=1}a_n\) сходиться, але ряд\(\displaystyle \sum^∞_{n=1}|a_n|\) розходиться,\(\displaystyle \sum^∞_{n=1}a_n\) то ряд, як кажуть, сходиться умовно
