9.2: Нескінченна серія
- Page ID
- 62211
- Поясніть значення суми нескінченного ряду.
- Обчисліть суму геометричного ряду.
- Оцініть телескопічну серію.
Ми бачили, що послідовність - це впорядкований набір термінів. Якщо ви додасте ці терміни разом, ви отримаєте серію. У цьому розділі ми визначаємо нескінченний ряд і показуємо, як серії пов'язані з послідовностями. Ми також визначаємо, що означає, що серія сходиться або розходиться. Ми представляємо один з найважливіших типів серій: геометричний ряд. Ми будемо використовувати геометричні ряди в наступному розділі, щоб записати певні функції як поліноми з нескінченною кількістю членів. Цей процес важливий, оскільки дозволяє нам оцінювати, диференціювати та інтегрувати складні функції за допомогою поліномів, які легше обробляти. Ми також обговорюємо гармонійну серію, можливо, найцікавішу розбіжну серію, оскільки вона просто не сходиться.
Суми та серії
Нескінченний ряд - це сума нескінченно багатьох термінів і пишеться у вигляді
\(\displaystyle \sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯.\)
Але що це означає? Ми не можемо додати нескінченну кількість термінів так само, як ми можемо додати кінцеву кількість термінів. Натомість значення нескінченного ряду визначається через межу часткових сум. Часткова сума нескінченного ряду - це скінченна сума виду
\(\displaystyle \sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k.\)
Щоб побачити, як ми використовуємо часткові суми для оцінки нескінченних рядів, розглянемо наступний приклад. Припустимо, нафта просочується в озеро таким чином, що\( 1000\) галони потрапляють в озеро перший тиждень. Протягом другого тижня в озеро надходить додаткові\( 500\) галони нафти. Третій тиждень в озеро надходить\( 250\) більше галонів. Припустимо, що ця закономірність триває так, що щотижня в озеро потрапляє вдвічі менше нафти, ніж на попередньому тижні. Якщо так триває вічно, що вже говорити про кількість нафти в озері? Чи буде кількість нафти продовжувати отримувати довільно велике, або можливо, що воно наближається до деякої кінцевої кількості? Щоб відповісти на це питання, ми розглянемо кількість нафти в озері після\( k\) тижнів. Даючи\( S_k\) позначити кількість нафти в озері (вимірюється тисячами галонів) через\( k\) тижні, ми бачимо, що
\( S_1=1\)
\( S_2=1+0.5=1+\frac{1}{2}\)
\( S_3=1+0.5+0.25=1+\frac{1}{2}+\frac{1}{4}\)
\( S_4=1+0.5+0.25+0.125=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}\)
\( S_5=1+0.5+0.25+0.125+0.0625=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}.\)
Дивлячись на цю закономірність, ми бачимо, що кількість нафти в озері (в тисячах галонів) через\( k\) тижні становить
\[ S_k=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+⋯+\frac{1}{2^{k−1}}=\sum_{n=1}^k\left(\frac{1}{2}\right)^{n−1}. \nonumber \]
Нас цікавить, що відбувається як\( k→∞.\) Символічно, кількість нафти в озері, як\( k→∞\) це дається нескінченним рядом
\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+⋯. \nonumber \]
У той же час, як\( k→∞\), кількість нафти в озері можна розрахувати, оцінивши\(\displaystyle \lim_{k→∞}S_k\). Тому поведінку нескінченного ряду можна визначити, дивлячись на поведінку послідовності часткових сум\( {S_k}\). Якщо послідовність часткових сум\( {S_k}\) сходиться, ми говоримо, що нескінченний ряд сходиться, а його сума задана\(\displaystyle \lim_{k→∞}S_k\). Якщо послідовність\( {S_k}\) розходиться, ми говоримо, що нескінченний ряд розходиться. Тепер звернемо увагу на визначення межі цієї послідовності\( {S_k}\).
По-перше, спрощуючи деякі з цих часткових сум, ми бачимо, що
\( S_1=1\)
\( S_2=1+\frac{1}{2}=\frac{3}{2}\)
\( S_3=1+\frac{1}{2}+\frac{1}{4}=\frac{7}{4}\)
\( S_4=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}=\frac{15}{8}\)
\( S_5=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}=\frac{31}{16}.\)
Поклавши деякі з цих значень на малюнку, виявляється, що послідовність\( {S_k}\) може наближатися до 2.
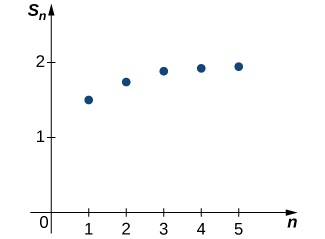
Давайте пошукаємо більш переконливі докази. У наступній таблиці ми перерахуємо значення\(S_k\) для декількох значень\(k\).
| \( k\) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| \( S_k\) | 1,9375 | 1.998 | 1,99939 | 1.9998 |
Ці дані дають більше доказів, що свідчать про те, що послідовність\({S_k}\) збігається до\(2\). Пізніше ми наведемо аналітичний аргумент, який можна використовувати, щоб довести це\(\displaystyle \lim_{k→∞}S_k=2\). Наразі ми покладаємося на числові та графічні дані, щоб переконати себе, що послідовність часткових сум насправді сходиться до\(2\). Оскільки ця послідовність часткових сум сходиться до\(2\), ми говоримо, що нескінченний ряд сходиться до\(2\) і записувати
\[ \sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2.\nonumber \]
Повертаючись до питання про нафту в озері, так як цей нескінченний ряд сходиться до\(2\), робимо висновок, що кількість нафти в озері буде довільно наближатися до\(2000\) галонів, так як кількість часу стає досить великим.
Ця серія є прикладом геометричного ряду. Більш докладно про геометричні ряди ми розглянемо далі в цьому розділі. Спочатку підсумовуємо, що означає сходитися нескінченний ряд.
Нескінченний ряд - це вираз форми
\[\sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯. \nonumber \]
Для кожного натурального цілого числа\(k\) - сума
\[S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k \nonumber \]
називається\(k^{\text{th}}\) частковою сумою нескінченного ряду. Часткові суми утворюють послідовність\({S_k}\). Якщо послідовність часткових сум сходиться до дійсного числа\(S\), нескінченний ряд сходиться. Якщо ми можемо описати збіжність ряду до\(S\), ми\(S\) називаємо суму ряду, і пишемо
\[\sum_{n=1}^∞a_n=S. \nonumber \]
Якщо послідовність часткових сум розходиться, ми маємо розбіжність ряду.
Зверніть увагу, що індекс для ряду не потрібно починати з,\(n=1\) а може починатися з будь-якого значення. Наприклад, серіал
\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1} \nonumber \]
також може бути записаний як
\[\sum_{n=0}^∞\left(\frac{1}{2}\right)^n\; \text{or}\; \sum_{n=5}^∞\left(\frac{1}{2}\right)^{n−5}. \nonumber \]
Часто індекс зручно починати з\(1\), тому якщо з якоїсь причини він починається з іншого значення, ми можемо повторно індексувати, зробивши зміну змінних. Для прикладу розглянемо серію
\[ \sum_{n=2}^∞\frac{1}{n^2}. \nonumber \]
Вводячи змінну\(m=n−1\), так що\(n=m+1,\) ми можемо переписати серію як
\[ \sum_{m=1}^∞\frac{1}{(m+1)^2}. \nonumber \]
Для кожного з наступних рядів використовуйте послідовність часткових сум, щоб визначити, чи збігається чи розходиться ряд.
- \(\displaystyle \sum_{n=1}^∞\frac{n}{n+1}\)
- \(\displaystyle \sum_{n=1}^∞(−1)^n\)
- \(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}\)
Рішення
а Послідовність часткових сум\({S_k}\) задовольняє
\(S_1=\dfrac{1}{2}\)
\(S_2=\dfrac{1}{2}+\dfrac{2}{3}\)
\(S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}\)
\(S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}\).
Зверніть увагу, що кожен доданий термін більше, ніж\(1/2\). В результаті ми бачимо, що
\(S_1=\dfrac{1}{2}\)
\(S_2=\dfrac{1}{2}+\dfrac{2}{3}>\dfrac{1}{2}+\dfrac{1}{2}=2\left(\dfrac{1}{2}\right)\)
\(S_3=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=3\left(\dfrac{1}{2}\right)\)
\(S_4=\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{4}{5}>\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}=4\left(\dfrac{1}{2}\right).\)
З цього шаблону ми бачимо, що\(S_k>k\left(\frac{1}{2}\right)\) для кожного цілого числа\(k\). Тому\({S_k}\) є необмеженим і, отже, розходиться. Тому нескінченний ряд\(\displaystyle \sum^∞_{n=1}\frac{n}{n+1}\) розходиться.
б. послідовність часткових сум\({S_k}\) задовольняє
\(S_1=−1\)
\(S_2=−1+1=0\)
\(S_3=−1+1−1=−1\)
\(S_4=−1+1−1+1=0.\)
З цієї закономірності ми можемо бачити послідовність часткових сум
\[{S_k}={−1,0,−1,0,…}. \nonumber \]
Оскільки ця послідовність розходиться, нескінченний ряд\(\displaystyle \sum^∞_{n=1}(−1)^n\) розходиться.
c Послідовність часткових сум\( {S_k}\) задовольняє
\( S_1=\dfrac{1}{1⋅2}=\dfrac{1}{2}\)
\( S_2=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}=\dfrac{1}{2}+\dfrac{1}{6}=\dfrac{2}{3}\)
\( S_3=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}=\dfrac{3}{4}\)
\( S_4=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}=\dfrac{4}{5}\)
\( S_5=\dfrac{1}{1⋅2}+\dfrac{1}{2⋅3}+\dfrac{1}{3⋅4}+\dfrac{1}{4⋅5}+\dfrac{1}{5⋅6}=\dfrac{5}{6}.\)
З цієї закономірності ми бачимо, що\( k^{\text{th}}\) часткова сума задається явною формулою
\[ S_k=\frac{k}{k+1} \nonumber \].
Оскільки\( k/(k+1)→1,\) ми робимо висновок, що послідовність часткових сум сходиться, і тому нескінченний ряд сходиться до\( 1\). У нас є
\[ \sum_{n=1}^∞\frac{1}{n(n+1)}=1. \nonumber \]
Визначте,\(\displaystyle \sum^∞_{n=1}\frac{n+1}{n}\) сходиться чи розходиться ряд.
- Підказка
-
Подивіться на послідовність часткових сум.
- Відповідь
-
Ряд розходиться через\( k^{\text{th}}\) часткову суму\( S_k>k\).
Гармонічна серія
Корисний серіал, про який слід знати, - це гармонійний ряд. Гармонічний ряд визначається як
\[\sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯. \nonumber \]
Цей серіал цікавий тим, що розходиться, але розходиться дуже повільно. Під цим ми маємо на увазі, що члени в послідовності часткових сум\( {S_k}\) наближаються до нескінченності, але роблять це дуже повільно. Ми покажемо, що ряд розходиться, але спочатку проілюструємо повільне зростання термінів в послідовності\( {S_k}\) в наступній таблиці.
| \( k\) | 10 | 100 | 1000 | 10,00 | 100 000 | 1 000 000 |
|---|---|---|---|---|---|---|
| \( S_k\) | 2.92897 | 5.18738 | 7.48547 | 9.78761 | 12.09.015 | 14 39273 |
Навіть після закінчення\( 1,000,000\) строків часткова сума все ще відносно невелика. З цієї таблиці незрозуміло, що цей ряд насправді розходиться. Однак аналітично можна показати, що послідовність часткових сум розходиться, і тому ряд розходиться.
Щоб показати, що послідовність часткових сум розходиться, показано, що послідовність часткових сум необмежена. Починаємо з написання перших декількох часткових сум:
\( S_1=1\)
\( S_2=1+\dfrac{1}{2}\)
\( S_3=1+\dfrac{1}{2}+\dfrac{1}{3}\)
\( S_4=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}\).
Зверніть увагу, що протягом останніх двох термінів в\( S_4\),
\[ \frac{1}{3}+\frac{1}{4}>\frac{1}{4}+\frac{1}{4} \nonumber \]
Тому робимо висновок, що
\[ S_4>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)=1+\frac{1}{2}+\frac{1}{2}=1+2\left(\frac{1}{2}\right). \nonumber \]
Використовуючи ту ж ідею для\( S_8\), ми бачимо, що
\(\displaystyle S_8=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>1+\frac{1}{2}+\left(\frac{1}{4}+\frac{1}{4}\right)+\left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right)=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=1+3\left(\frac{1}{2}\right)\).
З цієї викрійки ми бачимо, що\( S_1=1, S_2=1+1/2, S_4>1+2(1/2),\) і\( S_8>1+3(1/2)\). У загальному плані можна показати, що\( S_{2^j}>1+j(1/2)\) для всіх\( j>1\). Так як\( 1+j(1/2)→∞,\) робимо висновок, що\( {S_k}\) послідовність необмежена і тому розходиться. У попередньому розділі ми заявляли, що збіжні послідовності обмежені. Отже, оскільки\( {S_k}\) є необмеженим, він розходиться. Таким чином, гармонійний ряд розходиться.
Алгебраїчні властивості збіжних рядів
Оскільки сума збіжного нескінченного ряду визначається як межа послідовності, алгебраїчні властивості для рядів, перерахованих нижче, випливають безпосередньо з алгебраїчних властивостей послідовностей.
\(\displaystyle \sum_{n=1}^∞ b_n\)Дозволяти\(\displaystyle \sum_{n=1}^∞ a_n\) і бути збіжними рядами. Потім дотримуються наступні алгебраїчні властивості.
i. ряд\(\displaystyle \sum_{n=1}^∞(a_n+b_n)\) сходиться, і\(\displaystyle \sum^∞_{n=1}(a_n+b_n)=\sum^∞_{n=1}a_n+\sum^∞_{n=1}b_n.\) (правило суми)
II. Ряд\(\displaystyle \sum_{n=1}^∞(a_n−b_n)\) сходиться, і\(\displaystyle \sum^∞_{n=1}(a_n−b_n)=\sum^∞_{n=1}a_n−\sum^∞_{n=1}b_n.\) (Правило різниці)
III. Для будь-якого дійсного числа ряд\( c\)\(\displaystyle \sum_{n=1}^∞ca_n\) сходиться, і\(\displaystyle \sum^∞_{n=1}ca_n=c\sum^∞_{n=1}a_n\). (Постійне множинне правило)
Оцінити\(\displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right].\)
Рішення
Раніше ми показали, що
\[ \sum_{n=1}^∞\frac{1}{n(n+1)} = 1 \nonumber \]
і
\[ \sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=2. \nonumber \]
Оскільки обидва ці ряди сходяться, ми можемо застосувати властивості Note\(\PageIndex{1}\) для оцінки
\[\sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]. \nonumber \]
Використовуючи правило суми, запишіть
\(\displaystyle \sum_{n=1}^∞\left[\frac{3}{n(n+1)}+\left(\frac{1}{2}\right)^{n−2}\right]=\sum_{n=1}^∞\frac{3}{n(n+1)}+\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−2}.\)
Потім, використовуючи постійне кратне правило і суми вище, можна зробити висновок, що
\(\displaystyle \sum^∞_{n=1}\frac{3}{n(n+1)}+\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−2}=3\sum^∞_{n=1}\frac{1}{n(n+1)}+\left(\frac{1}{2}\right)^{−1}\sum^∞_{n=1}\left(\frac{1}{2}\right)^{n−1}=3(1)+\left(\frac{1}{2}\right)^{−1}(2)=3+2(2)=7.\)
Оцінити\(\displaystyle \sum^∞_{n=1}\frac{5}{2^{n−1}}\).
- Підказка
-
Перепишіть як\(\displaystyle \sum^∞_{n=1}5\left(\frac{1}{2}\right)^{n−1}\).
- Відповідь
-
10
Геометрична серія
Геометричний ряд - це будь-яка серія, яку ми можемо написати у формі
\[ a+ar+ar^2+ar^3+⋯=\sum_{n=1}^∞ar^{n−1}. \nonumber \]
Оскільки відношення кожного члена в цьому ряду до попереднього члена дорівнює r, число r називається співвідношенням. Ми називаємо a початковим терміном, оскільки це перший термін у серії. Наприклад, серіал
\[\sum_{n=1}^∞\left(\frac{1}{2}\right)^{n−1}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+⋯ \nonumber \]
являє собою геометричний ряд з початковим терміном\( a=1\) і співвідношенням\( r=1/2\).
Загалом, коли сходиться геометричний ряд? Розглянемо геометричні ряди
\[\sum_{n=1}^∞ar^{n−1} \nonumber \]
коли\( a>0\). Його послідовність часткових сум\( {S_k}\) задається
\[S_k=\sum_{n=1}^kar^{n−1}=a+ar+ar^2+⋯+ar^{k−1}. \nonumber \]
Розглянемо випадок, коли\( r=1.\) У такому випадку
\[S_k=a+a(1)+a(1)^2+⋯+a(1)^{k−1}=ak. \nonumber \]
З тих пір\( a>0\), ми знаємо\( ak→∞\) як\( k→∞\). Тому послідовність часткових сум необмежена і таким чином розходиться. Отже, нескінченний ряд розходиться за\( r=1\). Для того\( r≠1\), щоб знайти межу\( {S_k}\), помножте Рівняння на\( 1−r\). Роблячи так, ми бачимо, що
\[ (1−r)S_k=a(1−r)(1+r+r^2+r^3+⋯+r^{k−1})=a[(1+r+r^2+r^3+⋯+r^{k−1})−(r+r^2+r^3+⋯+r^k)]=a(1−r^k). \nonumber \]
Всі інші умови скасовуються.
Тому,
\( S_k=\dfrac{a(1−r^k)}{1−r}\)для\( r≠1\).
З нашого обговорення в попередньому розділі ми знаємо, що геометрична послідовність,\( r^k→0\) якщо\( |r|<1\) і що\( r^k\) розходиться, якщо\( |r|>1\) або\( r=±1\). Тому для\( |r|<1, S_k→\dfrac{a}{1−r}\) і у нас є
\[ \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{if}\; |r|<1. \nonumber \]
Якщо\( |r|≥1, S_k\) розходиться, а значить
\[ \sum_{n=1}^∞ar^{n−1} \; \text{diverges if}\; |r|≥1. \nonumber \]
Геометричний ряд - це серія форми
\[\sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯. \nonumber \]
Якщо\( |r|<1\), ряд сходиться, і
\[\sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\; \text{for}\; |r|<1. \nonumber \]
Якщо\( |r|≥1\), ряд розходиться.
Геометричні ряди іноді з'являються в дещо інших формах. Наприклад, іноді індекс починається зі значення, відмінного від\( n=1\) або експонента включає лінійний вираз для\( n\) іншого, ніж\( n−1\). Поки ми можемо переписати ряд у формі, заданій рівнянням, це геометричний ряд. Для прикладу розглянемо серію
\[\sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}. \nonumber \]
Щоб побачити, що це геометричний ряд, виписуємо перші кілька термінів:
\(\displaystyle \sum_{n=0}^∞\left(\frac{2}{3}\right)^{n+2}=\left(\frac{2}{3}\right)^2+\left(\frac{2}{3}\right)^3+\left(\frac{2}{3}\right)^4+⋯=\frac{4}{9}+\frac{4}{9}⋅\left(\frac{2}{3}\right)+\frac{4}{9}⋅\left(\frac{2}{3}\right)^2+⋯.\)
Ми бачимо, що початковий термін є\( a=4/9\) і співвідношення\( r=2/3.\) Тому ряд можна записати як
\(\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}.\)
Так як\( r=2/3<1\), цей ряд сходиться, а його сума задається
\(\displaystyle \sum_{n=1}^∞\frac{4}{9}⋅\left(\frac{2}{3}\right)^{n−1}=\frac{4/9}{1−2/3}=\frac{4}{3}.\)
Визначте, сходиться або розходиться кожен з наступних геометричних рядів, і якщо він сходиться, знайдіть його суму.
- \(\displaystyle \sum^∞_{n=1}\frac{(−3)^{n+1}}{4^{n−1}}\)
- \(\displaystyle \sum^∞_{n=1}e^{2n}\)
Рішення
а. виписуючи перші кілька термінів в серії, ми маємо
\[\begin{align*} \sum_{n=1}^∞\frac{(−3)^{n+1}}{4^{n−1}} &= \frac{(−3)^2}{4^0}+\frac{(−3)^3}{4}+\frac{(−3)^4}{4^2}+⋯ \\[4pt] &=(−3)^2+(−3)^2⋅\left(\frac{−3}{4}\right)+(−3)^2⋅\left(\frac{−3}{4}\right)^2+⋯ \\[4pt] &=9+9⋅\left(\frac{−3}{4}\right)+9⋅\left(\frac{−3}{4}\right)^2+⋯. \end{align*}\]
Початковий термін\( a=−3\) і співвідношення\( r=−3/4\). Так як\( |r|=3/4<1\), ряд сходиться до
\[ \frac{9}{1−(−3/4)}=\frac{9}{7/4}=\frac{36}{7}. \nonumber \]
б. написання цієї серії як
\[ e^2\sum_{n=1}^∞(e^2)^{n−1} \nonumber \]
ми бачимо, що це геометрична серія, де\( r=e^2>1.\) Тому серія розходиться.
Визначте,\(\displaystyle \sum_{n=1}^∞\left(\frac{−2}{5}\right)^{n−1}\) сходиться чи розходиться ряд. Якщо вона сходиться, знайдіть її суму.
- Підказка
-
\( r=−2/5\)
- Відповідь
-
\( 5/7\)
Тепер звернемо увагу на приємну аплікацію з геометричних рядів. Ми показуємо, як вони можуть бути використані для запису повторюваних десяткових дробів як дробів цілих чисел.
Використовуйте геометричний ряд, щоб записати\( 3.\bar{26}\) як дріб цілих чисел.
Рішення
Так як\( 3.\bar{26}—=3.262626…,\) спочатку ми пишемо
\[\begin{align*} 3.262626… &= 3+\frac{26}{100}+\frac{26}{1000}+\frac{26}{100,000}+⋯ \\[4pt] &=3+\frac{26}{10^2}+\frac{26}{10^4}+\frac{26}{10^6}+⋯. \end{align*}\]
Ігноруючи термін 3, решта цього виразу являє собою геометричний ряд з початковим терміном\( a=26/10^2\) і співвідношенням.\( r=1/10^2.\) Тому сума цього ряду дорівнює
\[ \frac{26/10^2}{1−(1/10^2)}=\frac{26/10^2}{99/10^2}=\frac{26}{99}. \nonumber \]
Таким чином,
\( 3.262626…=3+\frac{26}{99}=\frac{323}{99}\).
Запишіть\( 5.2\bar{7}\) як дріб цілих чисел.
- Підказка
-
Висловлюючи це число як ряд, знайдіть геометричний ряд з початковим терміном\( a=7/100\) і співвідношенням\( r=1/10\).
- Відповідь
-
\( 475/90\)
Визначте послідовність фігур\( \{F_n\}\) рекурсивно наступним чином (рис.\(\PageIndex{2}\)). \( F_0\)Дозволяти рівносторонній трикутник зі сторонами довжини\( 1\). Для\( n≥1\),\( F_n\) нехай крива створена шляхом видалення середньої третини кожної сторони\( F_{n−1}\) і замінивши її рівностороннім трикутником, спрямованим назовні. Гранична фігура\( n→∞\), як відома як сніжинка Коха.
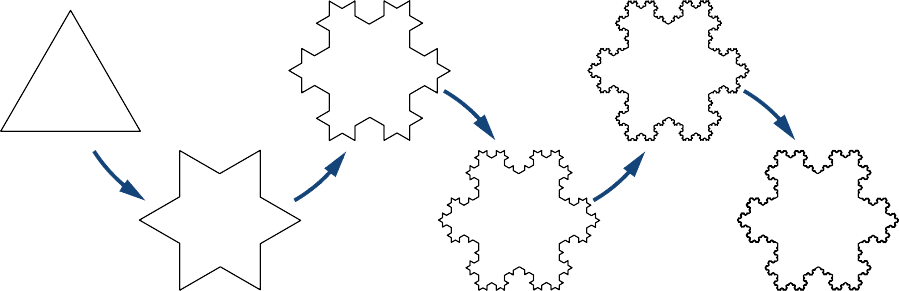
- Знайти\( L_n\) довжину периметра\( F_n\). Оцініть,\(\displaystyle \lim_{n→∞}L_n\) щоб знайти довжину периметра сніжинки Коха.
- Знайдіть\( A_n\) площу фігури\( F_n\). Оцініть,\(\displaystyle \lim_{n→∞}A_n\) щоб знайти площу сніжинки Коха.
Рішення
а. нехай\( N_n\) позначають кількість сторін фігури\( F_n\). Так як\( F_0\) це трикутник,\( N_0=3\). Нехай ln позначають довжину кожної сторони\( F_n\). Так як\( F_0\) це рівносторонній трикутник зі сторонами довжини\( l_0=1\), нам тепер потрібно визначити\( N_1\) і\( l_1\). Оскільки\( F_1\) створюється шляхом видалення середньої третини кожної сторони і замінивши цей відрізок лінії двома відрізками лінії, для кожної сторони\( F_0\), ми отримуємо чотири сторони в\( F_1\). Таким чином, кількість сторін для\( F_1\) становить
\( N_1=4⋅3\).
Оскільки довжина кожного з цих нових відрізків лінії\( 1/3\) дорівнює довжині відрізків лінії в\( F_0\), довжина відрізків лінії для\( F_1\) задається
\( l_1=\frac{1}{3}⋅1=\frac{1}{3}\).
Аналогічно\( F_2\), для, оскільки середня третина кожної сторони\( F_1\) видаляється і замінюється двома відрізками лінії, кількість сторін в\( F_2\) задається
\( N_2=4N_1=4(4⋅3)=4^2⋅3.\)
Так як довжина кожної з цих сторін дорівнює\( 1/3\) довжині сторін\( F_1\), то довжина кожної сторони фігури\( F_2\) задається
\( l_2=\frac{1}{3}⋅l_1=\frac{1}{3}⋅\frac{1}{3}=\left(\frac{1}{3}\right)^2\).
Більш загалом, оскільки\( F_n\) створюється шляхом видалення середньої третини кожної сторони\( F_{n−1}\) і заміна цього відрізка лінії двома відрізками довжини\( \frac{1}{3}l_{n−1}\) у формі рівностороннього трикутника, ми знаємо, що\( N_n=4N_{n−1}\) і\( l_n=\dfrac{l_{n−1}}{3}\). Тому кількість сторін фігури\( F_n\) дорівнює
\( N_n=4^n⋅3\)
і довжина кожної сторони
\[ l_n=\left(\frac{1}{3}\right)^n. \nonumber \]
Тому, щоб обчислити периметр\( F_n\), множимо кількість сторін\( N_n\) і довжину кожної сторони\( l_n\). Робимо висновок, що периметр\( F_n\) задається
\[ L_n=N_n⋅l_n=3⋅\left(\frac{4}{3}\right)^n \nonumber \]
Тому довжина периметра сніжинки Коха дорівнює
\[ L=\lim_{n→∞}L_n=∞. \nonumber \]
б. нехай\( T_n\) позначають площу кожного нового трикутника, створеного при формуванні\( F_n\). For\( n=0, T_0\) - площа вихідного рівностороннього трикутника. Тому,\( T_0=A_0=\sqrt{3}/4\). Бо\( n≥1\), оскільки довжини сторін нового\( 1/3\) трикутника є довжиною сторін\( F_{n−1}\), ми маємо
\[ T_n=\left(\frac{1}{3}\right)^2⋅T_{n−1}=\frac{1}{9}⋅T_{n−1}. \nonumber \]
Тому,\( T_n=\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}\). Так як з кожного боку утворюється новий трикутник\( F_{n−1}\),
\[ A_n=A_{n−1}+N_{n−1}⋅T_n=A_{n−1}+(3⋅4_{n−1})⋅\left(\frac{1}{9}\right)^n⋅\frac{\sqrt{3}}{4}=A_{n−1}+\frac{3}{4}⋅\left(\frac{4}{9}\right)^n⋅\frac{\sqrt{3}}{4}. \nonumber \]
Виписуючи перші кілька термінів,\( A_0,A_1,A_2,\) ми бачимо, що
\( A_0=\frac{\sqrt{3}}{4}\)
\(A_1=A_0+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}+\frac{3}{4}⋅\left(\frac{4}{9}\right)⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]\)
\( A_2=A_1+\frac{3}{4}⋅(\frac{4}{9})^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}⋅\left(\frac{4}{9}\right)\right]+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2⋅\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{4}[1+\frac{3}{4}⋅(\frac{4}{9})+\frac{3}{4}⋅\left(\frac{4}{9}\right)^2]\).
У загальному плані,
\( A_n=\frac{\sqrt{3}}{4}\left[1+\frac{3}{4}\left(\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^n\right)\right]\).
Факторинг\( 4/9\) кожного члена всередині внутрішніх дужок, ми переписуємо наш вираз як
\( A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}\left(1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}\right)\right]\).
Вираз\( 1+\left(\frac{4}{9}\right)+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}\) являє собою геометричну суму. Як було показано раніше, ця сума задовольняє
\( 1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+⋯+\left(\frac{4}{9}\right)^{n−1}=\dfrac{1−(4/9)^n}{1−(4/9)}.\)
Підставляючи цей вираз в вираз вище і спрощуючи, робимо висновок, що
\[ A_n=\frac{\sqrt{3}}{4}\left[1+\frac{1}{3}(\frac{1−(4/9)^n}{1−(4/9)})\right]=\frac{\sqrt{3}}{4}\left[\frac{8}{5}−\frac{3}{5}\left(\frac{4}{9}\right)^n\right]. \nonumber \]
Тому площа сніжинки Коха
\(\displaystyle A=\lim_{n→∞}A_n=\frac{2\sqrt{3}}{5}.\)
Аналіз
Сніжинка Коха цікава тим, що має кінцеву площу, але нескінченний периметр. Хоча спочатку це може здатися неможливим, нагадайте, що подібні приклади ви бачили раніше в тексті. Наприклад, розглянемо область, обмежену кривою\( y=1/x^2\) і\( x\) -вісь на інтервалі\( [1,∞).\) З неправильного інтеграла
\[ ∫^∞_1\frac{1}{x^2}\,dx \nonumber \]
сходиться, площа цієї області кінцева, хоча периметр нескінченний.
Телескопічна серія
Розглянемо серію\(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}.\) Ми розглянули цю серію на прикладі, показуючи, що ряд сходиться, виписуючи перші кілька часткових сум\( S_1,S_2,…,S_6\) і помічаючи, що всі вони мають форму\( S_k=\dfrac{k}{k+1}\). Тут ми використовуємо іншу техніку, щоб показати, що ця серія сходиться. Використовуючи часткові дроби, ми можемо записати
\[ \frac{1}{n(n+1)}=\frac{1}{n}−\frac{1}{n+1}. \nonumber \]
Тому серію можна записати як
\(\displaystyle \sum_{n=1}^∞\left[\frac{1}{n}−\frac{1}{n+1}\right]=\left(1+\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯.\)
Виписуючи перші кілька членів в послідовності часткових сум,\( {S_k},\) ми бачимо, що
\( S_1=1−\frac{1}{2}\)
\( S_2=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)=1−\frac{1}{3}\)
\( S_3=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)=1−\frac{1}{4}\).
Загалом,
\( S_k=\left(1−\frac{1}{2}\right)+\left(\frac{1}{2}−\frac{1}{3}\right)+\left(\frac{1}{3}−\frac{1}{4}\right)+⋯+\left(\frac{1}{k}−\frac{1}{k+1}\right)=1−\dfrac{1}{k+1}\).
Ми помічаємо, що середні терміни скасовують один одного, залишаючи тільки перший і останній терміни. У певному сенсі серія руйнується, як підзорне скло з трубками, які зникають один в одного, щоб вкоротити телескоп. З цієї причини ми називаємо серію, яка має цю властивість телескопічною серією. Для цього ряду, оскільки\( S_k=1−1/(k+1)\) і\( 1/(k+1)→0\) як\( k→∞\), послідовність часткових сум сходиться до\( 1\), і тому ряд сходиться до\( 1\).
Телескопічна серія - це серія, в якій більшість термінів скасовуються в кожній з часткових сум, залишаючи лише деякі перші терміни та деякі останні терміни.
Наприклад, будь-яка серія форми
\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)+⋯\)
являє собою телескопічну серію. Ми можемо переконатися в цьому, виписуючи частину часткових сум. Зокрема, ми бачимо, що
\( S_1=b_1−b_2\)
\( S_2=(b_1−b_2)+(b_2−b_3)=b_1−b_3\)
\( S_3=(b_1−b_2)+(b_2−b_3)+(b_3−b_4)=b_1−b_4.\)
Загалом, k-я часткова сума цього ряду дорівнює
\( S_k=b_1−b_{k+1}\).
Оскільки k-я часткова сума може бути спрощена до різниці цих двох членів, послідовність часткових сум\( {S_k}\) буде сходитися тоді і тільки в тому випадку, якщо послідовність\( {b_{k+1}}\) сходиться. Причому, якщо послідовність\( b_{k+1}\) сходиться до деякого скінченного числа B, то послідовність часткових сум сходиться до\( b_1−B\), а значить
\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−B.\)
У наступному прикладі ми покажемо, як використовувати ці ідеї для аналізу телескопічного ряду цієї форми.
Визначте, чи є телескопічна серія
\(\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]\)
сходиться або розходиться. Якщо вона сходиться, знайдіть її суму.
Рішення
Виписуючи терміни в послідовності часткових сум, ми можемо бачити, що
\( S_1=\cos(1)−\cos(\frac{1}{2})\)
\( S_2=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))=\cos(1)−\cos(\frac{1}{3})\)
\( S_3=(\cos(1)−\cos(\frac{1}{2}))+(\cos(\frac{1}{2})−\cos(\frac{1}{3}))+(\cos(\frac{1}{3})−\cos(\frac{1}{4}))\)
\( =\cos(1)−\cos(\frac{1}{4})\).
Загалом,
\( S_k=\cos(1)−\cos\left(\frac{1}{k+1}\right)\).
Оскільки\( 1/(k+1)→0\) як\( k→∞\) і\( \cos x\) є безперервною функцією,\( \cos(1/(k+1))→\cos(0)=1\). Тому робимо висновок, що\( S_k→\cos(1)−1\). Телескопічний ряд сходиться і сума задається
\(\displaystyle \sum_{n=1}^∞\left[\cos\left(\frac{1}{n}\right)−\cos\left(\frac{1}{n+1}\right)\right]=\cos(1)−1.\)
Визначте,\(\displaystyle \sum^∞_{n=1}[e^{1/n}−e^{1/(n+1)}]\) сходиться або розходиться. Якщо вона сходиться, знайдіть її суму.
- Підказка
-
Випишіть послідовність часткових сум, щоб побачити, які терміни скасовують.
- Відповідь
-
\( e−1\)
Ми показали, що гармонійний ряд\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) розходиться. Тут ми досліджуємо поведінку часткових сум\( S_k\) як\( k→∞.\) Зокрема, ми показуємо, що вони поводяться як функція натурального логарифма, показуючи, що існує константа\( γ\) така, що
\(\displaystyle \sum_{n=1}^k\left(\frac{1}{n}−\ln k\right)→γ\)як\( k→∞.\)
Ця константа\( γ\) відома як константа Ейлера.
1. Дозвольте\(\displaystyle T_k=\sum_{n=1}^k\left(\frac{1}{n}−\ln k\right).\) оцінювати\( T_k\) для різних значень\( k\).
2. Для\( T_k\) як визначено в частині 1. показати, що послідовність\( {T_k}\) збігається за допомогою наступних кроків.
a. показати, що послідовність\( {T_k}\) є монотонним зменшенням. (Підказка: Покажіть, що\( \ln(1+1/k>1/(k+1))\)
b. показати, що послідовність\( {T_k}\) обмежена нижче нулем. (Підказка: Експрес\( \ln k\) як певний інтеграл.)
c Використовуйте теорему про збіжність монотонних, щоб зробити висновок, що послідовність\( {T_k}\) сходиться. Межа\( γ\) - константа Ейлера.
3. Тепер оцініть, наскільки\( T_k\) далеко від\( γ\) заданого цілого числа\( k\). Доведіть, що\( k≥1, 0<T_k−γ≤1/k\) за допомогою наступних кроків.
a. показати, що\( \ln(k+1)−\ln k<1/k.\)
b Використовуйте результат з частини a., щоб показати, що для будь-якого цілого числа\( k\)
\[ T_k−T_{k+1}<\frac{1}{k}−\frac{1}{k+1}. \nonumber \]
c Для будь-яких цілих чисел\( k\) і\( j\) таких\( j>k\), що, висловити\( T_k−T_j\) як телескопічну суму шляхом написання
\[ T_k−T_j=(T_k−T_{k+1})+(T_{k+1}−T_{k+2})+(T_{k+2}−T_{k+3})+⋯+(T_{j−1}−T_j). \nonumber \]
Використовуйте результат частини б. у поєднанні з цією телескопічною сумою, щоб зробити висновок, що
\[ T_k−T_j<\frac{1}{k}−\frac{1}{j}. \nonumber \]
а) застосувати межу до обох сторін нерівності в частині c., щоб зробити висновок, що
\[ T_k−γ≤\frac{1}{k}. \nonumber \]
е.\( γ\) оцінити з точністю в межах 0,001.
Ключові поняття
- З огляду на нескінченний ряд
\(\displaystyle \sum_{n=1}^∞a_n=a_1+a_2+a_3+⋯\)
і відповідну послідовність часткових сум\( {S_k}\), де
\(\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k\),
ряд сходиться тоді і тільки в тому випадку, якщо послідовність\( {S_k}\) сходиться.
- Геометричний ряд\(\displaystyle \sum^∞_{n=1}ar^{n−1}\) сходиться, якщо\( |r|<1\) і розходиться, якщо\( |r|≥1.\) для\( |r|<1,\)
\(\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\).
- Гармонічний ряд
\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯\)
розходиться.
- Серія форми\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=[b_1−b_2]+[b_2−b_3]+[b_3−b_4]+⋯+[b_n−b_{n+1}]+⋯\) являє собою телескопічну серію. \( k^{\text{th}}\)Часткова сума цього ряду задається за допомогою\( S_k=b_1−b_{k+1}\). Ряд буде сходитися, якщо і тільки якщо\(\displaystyle \lim_{k→∞} b_{k+1}\) існує. У такому випадку
\(\displaystyle \sum_{n=1}^∞[b_n−b_{n+1}]=b_1−\lim_{k→∞}(b_{k+1})\).
Ключові рівняння
- Гармонічна серія
\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯\)
- Сума геометричного ряду
\(\displaystyle \sum_{n=1}^∞ar^{n−1}=\frac{a}{1−r}\)для\( |r|<1\)
Глосарій
- зближення ряду
- ряд сходиться, якщо послідовність часткових сум для цього ряду збігається
- розбіжність ряду
- ряд розходиться, якщо послідовність часткових сум для цього ряду розходиться
- геометрична серія
- геометричний ряд - це ряд, який можна записати у вигляді
\(\displaystyle \sum_{n=1}^∞ar^{n−1}=a+ar+ar^2+ar^3+⋯\)
- гармонійний ряд
- гармонійний ряд набуває вигляду
\(\displaystyle \sum_{n=1}^∞\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+⋯\)
- нескінченна серія
- нескінченний ряд - це вираз форми
\(\displaystyle a_1+a_2+a_3+⋯=\sum_{n=1}^∞a_n\)
- часткова сума
-
\( kth\)часткова сума нескінченного ряду\(\displaystyle \sum^∞_{n=1}a_n\) - скінченна сума
\(\displaystyle S_k=\sum_{n=1}^ka_n=a_1+a_2+a_3+⋯+a_k\)
- телескопічна серія
- телескопічний ряд - це той, в якому більшість термінів скасовуються в кожній з часткових сум
