6.2: Визначення обсягів шляхом нарізки

Last updated
Save as PDF

Page ID: 61648

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте обсяг твердого тіла шляхом інтеграції поперечного перерізу (метод нарізки).
Знайти обсяг твердого тіла обертання за допомогою дискового методу.
Знайти обсяг твердого тіла обертання з порожниною за допомогою методу шайби.

У попередньому розділі ми використовували певні інтеграли, щоб знайти площу між двома кривими. У цьому розділі ми використовуємо певні інтеграли для пошуку об'ємів тривимірних тіл. Розглянуто три підходи — нарізка, диски та шайби — для знаходження цих обсягів залежно від характеристик твердого тіла.

Обсяг і спосіб нарізки

Подібно до того, як площа є числовою мірою двовимірної області, об'єм є числовою мірою тривимірного твердого тіла. Більшість з нас обчислили обсяги твердих тіл за допомогою основних геометричних формул. Обсяг прямокутного твердого тіла, наприклад, можна обчислити шляхом множення довжини, ширини та висоти:$V=lwh.$ Формули для обсягів:

сфера

\[V_{sphere}=\dfrac{4}{3}πr^3, \nonumber \]

конус

\[V_{cone}=\dfrac{1}{3}πr^2h \nonumber \]

і піраміда

\[V_{pyramid}=\dfrac{1}{3}Ah \nonumber \]

також були введені. Хоча деякі з цих формул були отримані лише за допомогою геометрії, всі ці формули можна отримати за допомогою інтеграції.

Ми також можемо обчислити обсяг циліндра. Хоча більшість з нас думає про циліндр як про круглу основу, таку як банка для супу або металевий стрижень, в математиці слово циліндр має більш загальне значення. Щоб обговорити циліндри в цьому більш загальному контексті, нам спочатку потрібно визначити певний словниковий запас.

Визначимо перетин твердого тіла, щоб бути перетином площини з твердим тілом. Циліндр визначається як будь-яке тверде тіло, яке може бути утворено шляхом перекладу площини області вздовж лінії, перпендикулярної області, яка називається віссю циліндра. Таким чином, всі поперечні перерізи, перпендикулярні осі циліндра, ідентичні. Тверде тіло, показане на малюнку,$\PageIndex{1}$ є прикладом циліндра з некруглим підставою. Щоб обчислити обсяг циліндра, ми просто множимо площу поперечного перерізу на висоту циліндра:$V=A⋅h.$ У випадку правого круглого циліндра (супова банка) це стає$V=πr^2h.$

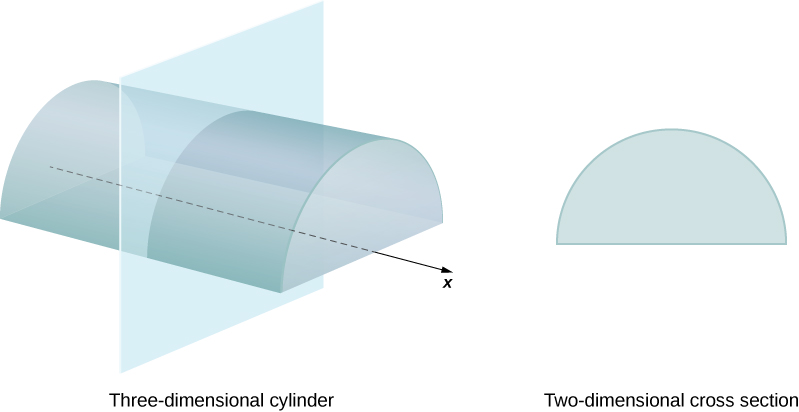
Ця графіка має дві цифри. Перша цифра - половина циліндра, на плоскій частині. Циліндр має лінію через центр з позначкою «х». Вертикально прорізаючи циліндр, перпендикулярно лінії - площину. Друга цифра - це двомірний перетин циліндра, що перетинається з площиною. Вона являє собою півколо. — Малюнок$\PageIndex{1}$*: Кожне перетин конкретного циліндра ідентично іншим.*

Якщо тверде тіло не має постійного перетину (і воно не є одним з інших основних твердих тіл), у нас може не бути формули його обсягу. У цьому випадку ми можемо використовувати певний інтеграл для обчислення обсягу твердого тіла. Ми робимо це, розрізаючи тверду речовину на шматки, оцінюючи обсяг кожного скибочки, а потім додаючи ці розрахункові обсяги разом. Зрізи все повинні бути паралельні один одному, і коли ми складемо всі скибочки разом, у нас повинна вийти ціла суцільна. Розглянемо, наприклад, тверде тіло S, показане на малюнку$\PageIndex{2}$, що проходить уздовж$x$ -осі.

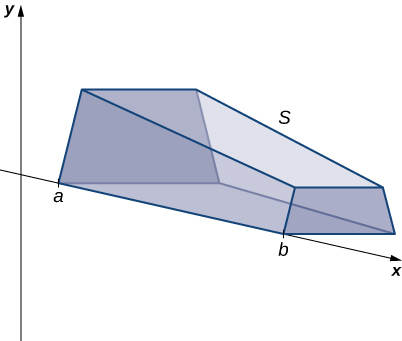
Ця цифра являє собою графік 3-вимірного твердого тіла. Вона має один край по осі х. Вісь x є частиною двовимірної системи координат з позначеною віссю y. Край твердого тіла вздовж осі x починається в точці з позначкою «a» і зупиняється в точці з позначкою «b». — Малюнок$\PageIndex{2}$: Тверда речовина з різним перетином.

Ми хочемо$S$ розділити на зрізи перпендикулярно $x$-осі. Як ми бачимо пізніше в розділі, можуть бути випадки, коли ми хочемо розрізати тверде тіло в якомусь іншому напрямку - скажімо, з фрагментами, перпендикулярними до$y$ осі. Рішення того, яким способом нарізати тверду речовину, дуже важливо. Якщо ми зробимо неправильний вибір, обчислення можуть стати досить безладними. Пізніше в розділі ми детально розглянемо деякі з цих ситуацій і розглянемо, як вирішити, яким способом нарізати тверде тіло. Однак для цілей цього розділу ми використовуємо фрагменти, перпендикулярні$x$ -осі.

Оскільки площа поперечного перерізу не є постійною, ми дозволяємо$A(x)$ представляти площу поперечного перерізу в точці х, Тепер нехай$P={x_0,x_1…,X_n}$ буде регулярний розділ$[a,b]$, і для$i=1,2,…n$, нехай$S_i$ представляють зріз$S$ розтягування від$x_{i−1}$ до$x_i$. На наступному малюнку показана нарізана суцільна с$n=3$.

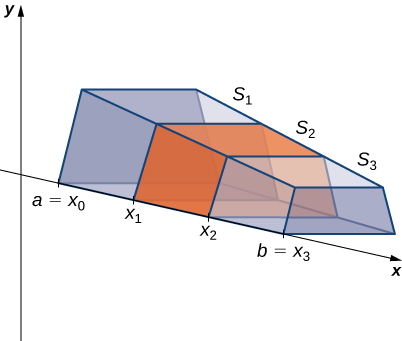
Нарешті, для$i=1,2,…n,$ нехай$x^∗_i$ буде довільна точка в$[x_{i−1},x_i]$. Тоді обсяг зрізу$S_i$ можна оцінити по$V(S_i)≈A(x^∗_i)\,Δx$. Склавши ці наближення разом, ми бачимо, що обсяг всього твердого тіла$S$ може бути наближений

\[V(S)≈\sum_{i=1}^nA(x^∗_i)\,Δx. \nonumber \]

На даний момент ми можемо визнати це як суму Рімана, і наш наступний крок - взяти межу, як$n→∞.$ Тоді ми маємо

\[V(S)=\lim_{n→∞}\sum_{i=1}^nA(x^∗_i)\,Δx=∫_a^b A(x)\,dx. \nonumber \]

Техніка, яку ми щойно описали, називається методом нарізки. Для його застосування ми використовуємо наступну стратегію.

Стратегія вирішення проблем: пошук обсягів методом нарізки

Огляньте тверде тіло і визначте форму поперечного перерізу твердого тіла. Часто корисно намалювати малюнок, якщо такий не передбачено.
Визначаємо формулу площі перетину.
Інтегруйте формулу площі протягом відповідного інтервалу, щоб отримати гучність.

Нагадаємо, що в цьому розділі ми припускаємо, що зрізи розташовуються перпендикулярно$x$ -осі. Тому формула площі знаходиться через x, а межі інтеграції лежать на $x$-осі. Однак наведена тут стратегія вирішення проблем дійсна незалежно від того, як ми вирішимо розрізати тверде тіло.

Приклад$\PageIndex{1}$: Deriving the Formula for the Volume of a Pyramid

З геометрії ми знаємо, що формула об'єму піраміди є$V=\dfrac{1}{3}Ah$. Якщо піраміда має квадратну основу$V=\dfrac{1}{3}a^2h$, то це стає, де a позначає довжину однієї сторони підстави. Ми будемо використовувати метод нарізки, щоб отримати цю формулу.

Рішення

Ми хочемо застосувати метод нарізки до піраміди з квадратною основою. Щоб встановити інтеграл, розглянемо піраміду, зображену на малюнку$\PageIndex{4}$, орієнтовану вздовж $x$-осі.

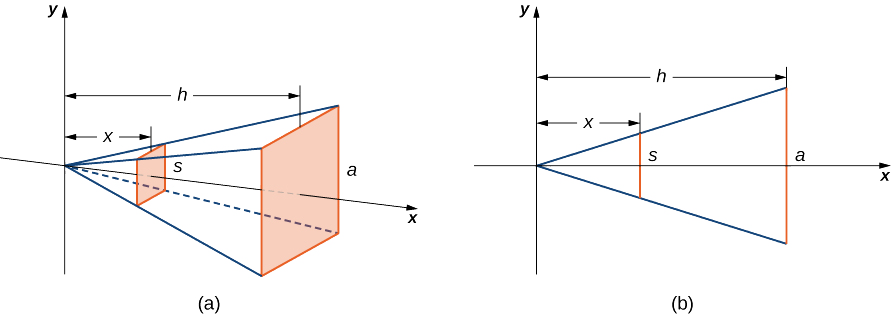
Ця цифра має два графіки. Перший граф, позначений «а», являє собою піраміду на її стороні. Вісь X проходить через середину піраміди. Точка вершини піраміди знаходиться на початку системи координат x y. Підстава піраміди затінюється і маркується «а». Усередині піраміди знаходиться затінений прямокутник з написом «s». Відстань від осі y до основи піраміди позначається як «h». Відстань прямокутника всередині піраміди до осі y позначається як «x». Друга фігура являє собою поперечний переріз піраміди з позначеними осями x і y. Перетин являє собою трикутник з однією стороною з позначкою «а», перпендикулярний осі х. Відстань a від осі y дорівнює h, є ще одна перпендикулярна лінія до осі x всередині трикутника. Він має маркування «s». Він дорівнює одиницям x від осі y. — Малюнок$\PageIndex{4}$: (а) Піраміда з квадратною основою орієнтована вздовж$x$ -осі. (б) Двовимірний вид піраміди видно збоку.

Спочатку хочемо визначити форму поперечного перерізу піраміди. Ми знаємо, що основа - квадрат, тому поперечні перерізи також квадрати (крок 1). Тепер ми хочемо визначити формулу площі одного з цих квадратів поперечного перерізу. Дивлячись на рисунок$\PageIndex{4}$ (b) і використовуючи пропорцію, оскільки це схожі трикутники, ми маємо

\[\dfrac{s}{a}=\dfrac{x}{h} \nonumber \]

або

\[s=\dfrac{ax}{h}. \nonumber \]

Тому площа одного з квадратів поперечного перерізу дорівнює

\[A(x)=s^2=\left(\dfrac{ax}{h}\right)^2 \quad\quad\text{(step 2)} \nonumber \]

Потім знаходимо обсяг піраміди шляхом інтеграції від$0$ до$h$ (крок 3):

\[V=∫_0^hA(x)\,dx=∫_0^h\left(\dfrac{ax}{h}\right)^2\,dx=\dfrac{a^2}{h^2}∫_0^hx^2\,dx=\left.\Big[\dfrac{a^2}{h^2}\left(\dfrac{1}{3}x^3\right)\Big]\right|^h_0=\dfrac{1}{3}a^2h. \nonumber \]

Це формула, яку ми шукали.

Вправа$\PageIndex{1}$

Скористайтеся методом нарізки, щоб вивести\[V=\dfrac{1}{3}πr^2h \nonumber \] формулу об'єму круглого конуса.

Підказка: Використовуйте подібні трикутники, як у прикладі$\PageIndex{1}$.

Тверді тіла революції

Якщо область в площині обертається навколо лінії в цій площині, отримане тверде тіло називається твердим тілом обертання, як показано на наступному малюнку.

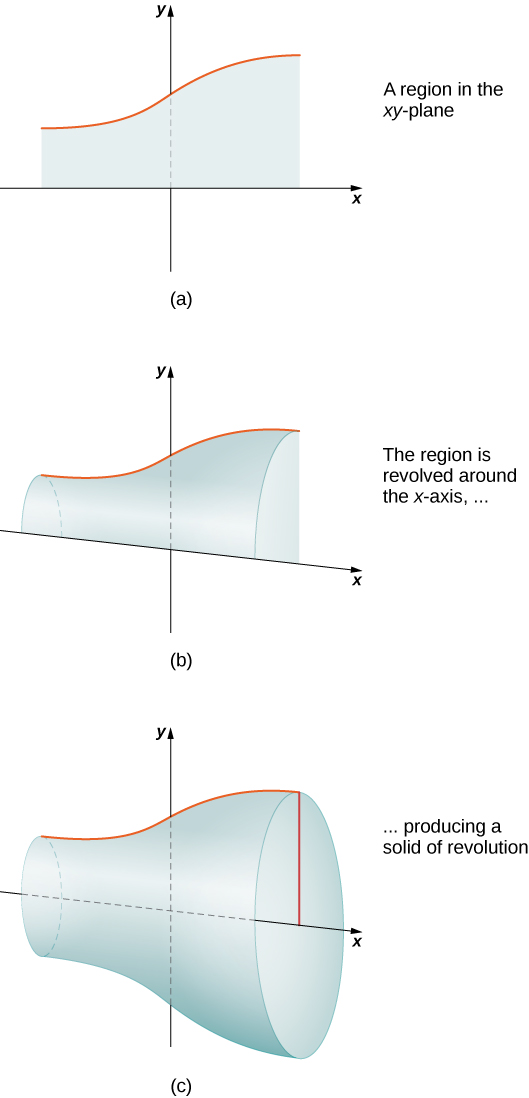
Ця цифра має три графіки. Перший граф, позначений «a», є областю в площині x y. Область створюється кривою над віссю x та віссю x. Другий графік, позначений «b», є тією ж областю, що і в «a», але він показує область, яка починає обертатися навколо осі x. Третій графік, позначений «c» - це тверде тіло, утворене обертанням області від «а» повністю навколо осі х, утворюючи тверде тіло. — Малюнок$\PageIndex{5}$: (а) Це область, яка обертається навколо$x$ -осі. (b) Коли область починає обертатися навколо осі, вона змітає тверду речовину обертання. (c) Це тверда речовина, яка виникає, коли революція завершена.

Тверді тіла обертання поширені в механічних додатках, таких як деталі машин, виготовлені токарним верстатом. Іншу частину цього розділу ми проводимо, дивлячись на тверді речовини цього типу. У наступному прикладі використовується метод нарізки для обчислення обсягу твердого тіла обертання.

Приклад$\PageIndex{2}$: Using the Slicing Method to find the Volume of a Solid of Revolution

Використовуйте метод нарізки, щоб знайти об'єм твердого тіла обертання$f(x)=x^2−4x+5,x=1$, обмеженого графіками$x=4,$ і поверненого навколо$x$ -осі.

Рішення

Використовуючи стратегію розв'язання задач, ми спочатку намалюємо графік квадратичної функції через інтервал,$[1,4]$ як показано на наступному малюнку.

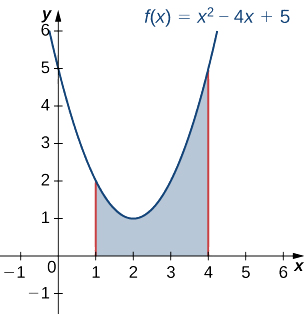
Ця цифра є графом параболи f (x) =x^2-4x+5. Парабола - це вершина затіненої області над віссю x. Область обмежена ліворуч лінією з x = 1, а праворуч - лінією з x = 4. — Малюнок$\PageIndex{6}$: Область, яка використовується для отримання твердого тіла революції.

Далі обертаємо область навколо$x$ -осі, як показано на наступному малюнку.

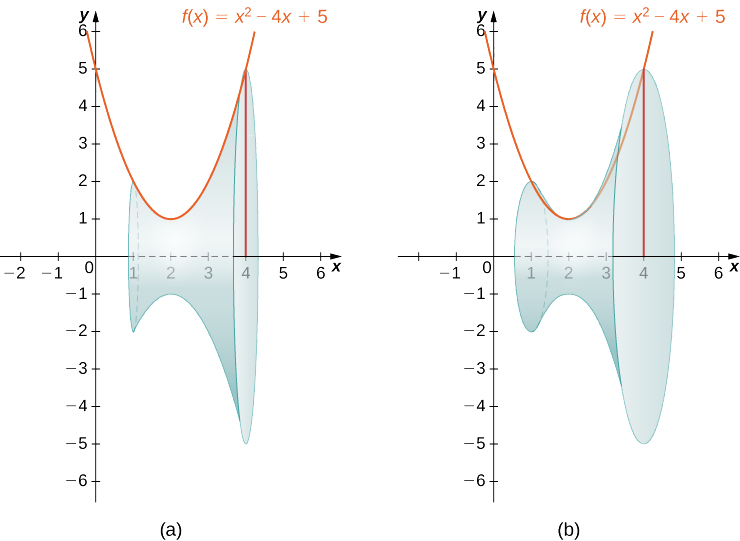
Ця цифра має два графіки параболи f (x) =x^2-4x+5. Парабола - це вершина затіненої області над віссю x. Область обмежена ліворуч лінією з x = 1, а праворуч - лінією з x = 4. Перший графік має затінене тверде тіло під параболою. Це тверде тіло було утворено обертанням параболи навколо осі х. Другий графік такий же, як і перший, при цьому тверде тіло обертається, щоб показати тверде тіло. — Малюнок$\PageIndex{7}$: Два види, (а) і (b), твердого тіла обертання, виробленого обертанням області на малюнку$\PageIndex{6}$ про$x$ **-вісь.**

Оскільки тверде тіло утворилося обертанням області навколо$x$ -осі, то поперечні перерізи є колами (крок 1). Площа перерізу, значить, - площа кола, а радіус кола задається за$f(x).$ допомогою формули площі кола:

\[A(x)=πr^2=π[f(x)]^2=π(x^2−4x+5)^2\quad\quad\text{(step 2).} \nonumber \]

Тоді обсяг дорівнює (крок 3)

\[\begin{align*} V &=∫_a^b A(x)\,dx \\ &=∫^4_1π(x^2−4x+5)^2\,dx \\ &=π∫^4_1(x^4−8x^3+26x^2−40x+25)\,dx \\ &=\left. π\left(\dfrac{x^5}{5}−2x^4+\dfrac{26x^3}{3}−20x^2+25x\right)\right|^4_1 \\ &=\dfrac{78}{5}π \end{align*}\]

Обсяг становить$78π/5\,\text{units}^3.$

Вправа$\PageIndex{2}$

Використовують метод нарізки, щоб знайти об'єм твердого тіла обертання, утвореного обертанням області між графіком функції$f(x)=1/x$ і$x$ -віссю над інтервалом$[1,2]$ навколо$x$ -осі. Дивіться наступний малюнок.

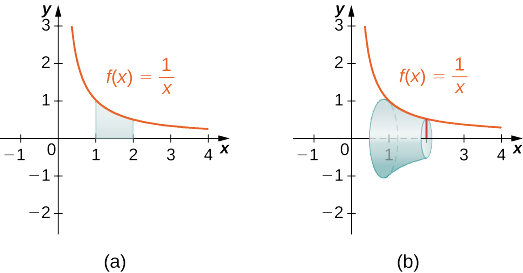
$Ця цифра має два графіки. Першим графіком є крива f (x) =1/x, крива зменшення над віссю x у першому квадранті. Графік має затінену область під кривою між x=1 та x=2. Другий графік - це крива f (x) =1/x в першому квадранті. Крім того, під цим графіком є тверде тіло між x = 1 і x = 2, яке було утворено обертанням області з першого графіка навколо осі x.$

Підказка: Використовуйте стратегію вирішення проблем, представлену раніше, і дотримуйтесь Прикладу$\PageIndex{2}$, щоб допомогти з кроком 2.

Відповідь: $\dfrac{π}{2} \,\text{units}^3$

Дисковий метод

Коли ми використовуємо метод нарізки з твердими частинами обертання, його часто називають дисковим методом, оскільки для твердих тіл обертання зрізи, які використовуються для перевищення обсягу твердого тіла, є дисками. Щоб побачити це, розглянемо тверде тіло обертання, породжене обертанням області між графіком функції$f(x)=(x−1)^2+1$ та $x$-віссю над інтервалом$[−1,3]$ навколо$x$ -осі. Графік функції і представницького диска наведені на малюнку$\PageIndex{8}$ (а) і (б). Область обертання і отримане тверде тіло показані на малюнку$\PageIndex{8}$ (в) і (г).

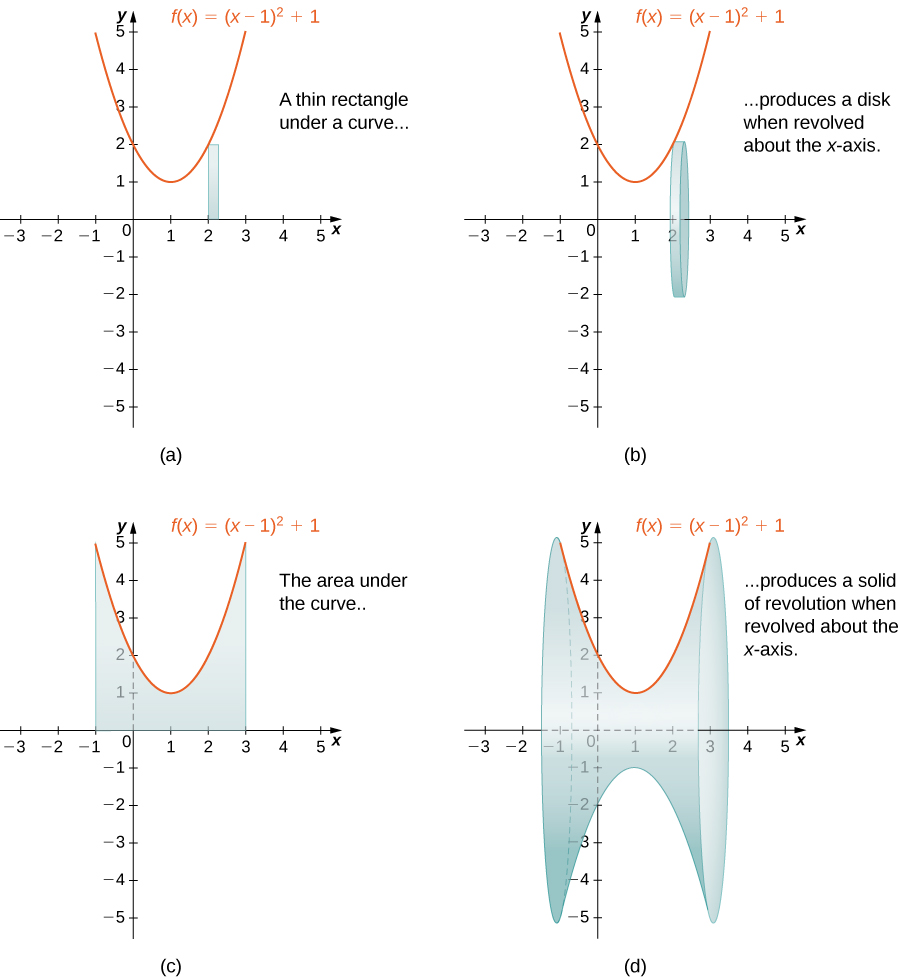
Ця цифра має чотири графіки. Перший граф, позначений «a», є параболою f (x) = (x-1) ^2+1. Крива знаходиться над віссю x і перетинає вісь y при y = 2. Під кривою в першому квадранті знаходиться вертикальний прямокутник, що починається з осі х і зупиняється на кривій. Другий графік, позначений «b», є такою ж параболою, що і на першому графіку. Прямокутник під параболою з першого графіка був повернутий навколо осі x, утворюючи суцільний диск. Третій граф з позначкою «c» - така ж парабола, що і перший граф. Вгорі є затінена область, обмежена параболою, ліворуч лінією x = -1 і праворуч лінією x = 3, а нижче - віссю x. Четвертий граф з позначкою «d» - це та ж парабола, що і перший граф. Область з третього графіка була обернена навколо осі x, утворюючи тверде тіло. — Рисунок$\PageIndex{8}$: (а) Тонкий прямокутник для наближення площі під кривою. (b) Представницький диск, утворений обертанням прямокутника навколо$x$ **-осі.** (c) Область під кривою обертається навколо$x$ **-осі,** в результаті чого (d) тверде тіло обертання.

Рисунок$\PageIndex{8}$: (e) Динамічна версія цього твердого тіла обертання, сформована за допомогою CalcPlot3D.

Ми вже використовували формальну розробку суми Рімана формули об'єму при розробці методу нарізки. Ми знаємо, що\[∫_a^b A(x)\,dx.\nonumber \]

Єдина відмінність від дискового методу полягає в тому, що ми знаємо формулу площі поперечного перерізу завчасно; це площа кола. Це дає наступне правило.

Дисковий метод

$f(x)$Дозволяти бути безперервним і невід'ємним. Визначте$R$ як область, обмежену вище графіком$f(x)$, нижче$x$ - віссю, зліва від лінії$x=a$, а праворуч - лінією$x=b$. Потім обсяг твердого тіла обертання, утвореного обертанням$R$ навколо$x$ -осі, задається

\[V=∫^b_aπ[f(x)]^2\,dx. \nonumber \]

Обсяг досліджуваного нами твердого тіла (рис.$\PageIndex{8}$) задається

\ [\ почати {вирівнювати*} V &=^b_aπ\ ліворуч [f (x)\ праворуч] ^2\, dx\\
&=^3_ {−1} π\ великий [(x−1) ^2+1\ великий] ^2\, dx=π^3_ {−1}\ великий [(x−1) ^4+2 (x−1) ^2+1 великий] ^2\, дх\\
&= π\ ліворуч. \ Великий [\ розрив {1} {5} (x−1) ^5+\ розрив {2} {3} (x−1) ^3+x\ Великий]\ праворуч |^3_ {−1}\\
&= π\ ліворуч [\ frac {32} {5} +\ frac {16} {3} +3\ праворуч) −\ ліворуч (\\ frac {32} {5} −\ розрив {16} {3} −1\ праворуч)\\
&=\ frac {412π} {15}\,\ text {одиниці} ^3. \ end {вирівнювати*}\]

Давайте розглянемо кілька прикладів.

Приклад$\PageIndex{3}$: Using the Disk Method to Find the Volume of a Solid of Revolution 1

Використовуйте метод диска, щоб знайти об'єм твердого тіла обертання, що генерується обертанням області між графіком$f(x)=\sqrt{x}$ і$x$ -віссю через інтервал$[1,4]$ навколо$x$ -осі.

Рішення

Графіки функції і твердого тіла обертання показані на наступному малюнку.

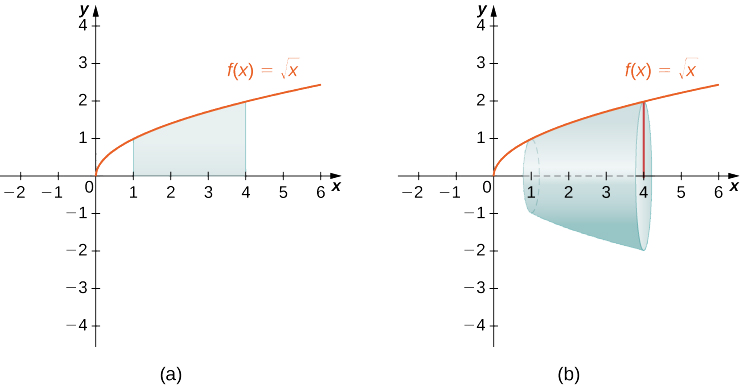
Ця цифра має два графіки. Перший граф з міткою «a» - це крива f (x) = квадратний корінь (x). Це зростаюча крива над віссю х. Крива знаходиться в першому квадранті. Під кривою знаходиться область, обмежена x=1 і x=4. Дно області - вісь х. Другий графік, позначений «b», є тією ж кривою, що і перший графік. Тверда область з першого графіка була повернута навколо осі x, утворюючи тверду область. — Малюнок$\PageIndex{9}$: (a) Функція$f(x)=\sqrt{x}$ за інтервалом$[1,4]$. (б) Тверде тіло обертання, отримане обертанням області під графіком$f(x)$ приблизно$x$ **-осі**.

У нас є

\ [\ почати {вирівнювати*} V & = ^b_Aπ\ великий [f (x)\ великий] ^2\, дх\\
&= ^4_1π\ ліворуч [\ sqrt {x}\ праворуч] ^2\, dx = π^4_1x\, dx\\
&=\ dfrac {π} {2} x^2\ big|^4_1x\ =\ dfrac {15π} {2}\ кінець {вирівнювати*}\]

Обсяг становить$(15π)/2 \,\text{units}^3.$

Вправа$\PageIndex{3}$

Використовуйте метод диска, щоб знайти об'єм твердого тіла обертання, що генерується обертанням області між графіком$f(x)=\sqrt{4−x}$ і$x$ -віссю через інтервал$[0,4]$ навколо$x$ -осі.

Підказка: Скористайтеся процедурою з Прикладу$\PageIndex{3}$.

Відповідь: $8π \,\text{units}^3$

Поки що в наших прикладах всі зацікавлені області обертаються навколо$x$ -осі, але ми можемо генерувати тверду силу обертання, обертаючи площину області навколо будь-якої горизонтальної або вертикальної лінії. У наступному прикладі ми розглянемо тверду речовину обертання, яка була породжена обертанням області навколо$y$ -осі. Механіка методу диска майже така ж, як коли$x$ -вісь є віссю обертання, але ми виражаємо функцію з точки зору$y$ і інтегруємо відносно y, а також. Це резюмується в наступному правилі.

Правило: Дисковий метод для твердих тіл обертання навколо$y$-axis

$g(y)$Дозволяти бути безперервним і невід'ємним. Визначте$Q$ як область, обмежену праворуч графіком$g(y)$, ліворуч$y$ - віссю, нижче лінією$y=c$ і вище лінією$y=d$. Потім обсяг твердого тіла обертання, утвореного обертанням$Q$ навколо$y$ -осі, задається

\[V=∫^d_cπ\big[g(y)\big]^2\,dy. \nonumber \]

Наступний приклад показує, як це правило працює на практиці.

Приклад$\PageIndex{4}$: Using the Disk Method to Find the Volume of a Solid of Revolution 2

$R$Дозволяти область обмежена графіком$g(y)=\sqrt{4−y}$ і$y$ -вісь над інтервалом$y$ -осі$[0,4]$. Використовуйте метод диска, щоб знайти об'єм твердого тіла обертання, що генерується$R$ обертанням навколо$y$ -осі.

Рішення

$\PageIndex{10}$На малюнку показана функція і представницький диск, який можна використовувати для оцінки обсягу. Зверніть увагу, що оскільки ми обертаємо функцію навколо$y$ -осі, диски горизонтальні, а не вертикальні.

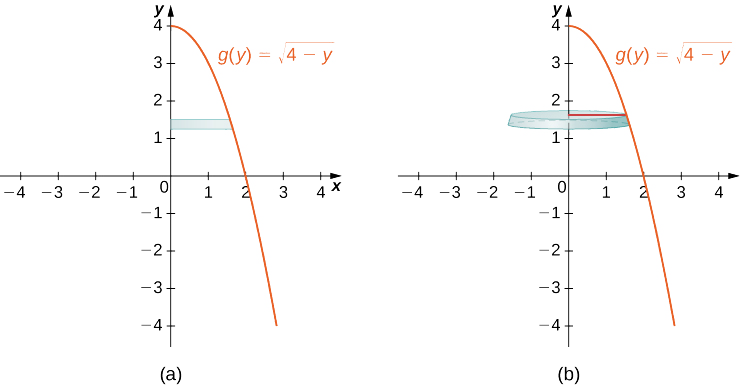
Ця цифра має два графіки. Перший граф з міткою «a» - це крива g (y) = квадратний корінь (4-y). Це крива, що зменшується, починаючи з осі y при y = 4. Між кривою і віссю y розташований горизонтальний прямокутник. Прямокутник починається з осі y і зупиняється на кривій. Другий графік, позначений «b», є тією ж кривою, що і перший графік. Прямокутник з першого графіка був повернутий навколо осі y, утворюючи горизонтальний диск. — Рисунок$\PageIndex{10}$: (a) Показаний тонкий прямокутник між кривою функції$g(y)=\sqrt{4−y}$ і$y$ **-віссю.** (b) Прямокутник утворює репрезентативний диск після обертання навколо$y$ **-осі.**

Регіон, який слід обертати, і повна тверда революція зображені на наступному малюнку.

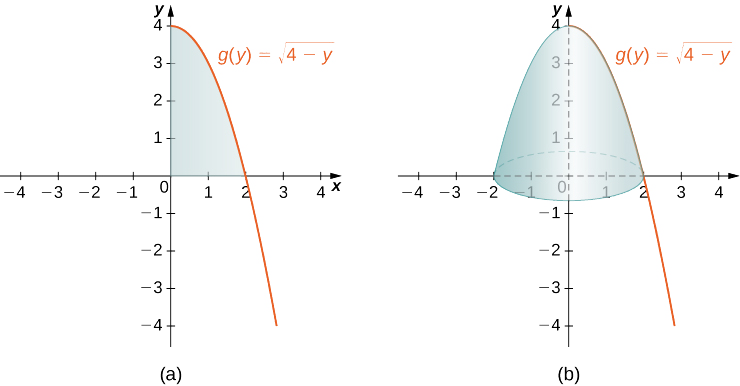
Ця цифра має два графіки. Перший граф з міткою «a» - це крива g (y) = квадратний корінь (4-y). Це крива, що зменшується, починаючи з осі y при y = 4. Область, утворена віссю x, віссю y та кривою затінюється. Цей регіон знаходиться в першому квадранті. Другий графік, позначений «b», є тією ж кривою, що і перший графік. Область з першого графіка була повернута навколо осі y, утворюючи тверде тіло. — Рисунок$\PageIndex{11}$: (a) Область зліва від функції$g(y)=\sqrt{4−y}$ над інтервалом$y$ -осі$[0,4]$. (b) Тверда речовина обертання, утворена обертанням області навколо$y$ -осі.

Щоб знайти обсяг, ми інтегруємо по відношенню до$y$. Отримуємо

\[V=∫^d_cπ\big[g(y)\big]^2\,dy=∫^4_0π\left[\sqrt{4−y}\right]^2\,dy=π∫^4_0(4−y)\,dy=π\left.\left[4y−\frac{y^2}{2}\right]\right|^4_0=8π. \nonumber \]

Обсяг є$8π \,\text{units}^3$.

Вправа$\PageIndex{4}$

Використовуйте метод диска, щоб знайти об'єм твердого тіла обертання, що генерується обертанням області між графіком$g(y)=y$ і$y$ -віссю через інтервал$[1,4]$ навколо$y$ -осі.

Підказка: Скористайтеся процедурою з Прикладу$\PageIndex{4}$.

Відповідь: $21π \,\text{units}^3$

Метод шайби

Деякі тверді тіла обертання мають порожнини посередині; вони не є твердими аж до осі обертання. Іноді це лише результат того, як область обертання формується щодо осі обертання. В інших випадках порожнини виникають, коли область обертання визначається як область між графіками двох функцій. Третім способом це може статися, коли вибирається вісь обертання, відмінна від $x$-осі або $y$-осі.

Коли тверде тіло обертання має порожнину посередині, зрізи, використовувані для наближення обсягу, - це не диски, а шайби (диски з отворами в центрі). Наприклад, розглянемо область, обмежену вище графіком функції,$f(x)=\sqrt{x}$ а нижче - графіком функції$g(x)=1$ за інтервалом$[1,4]$. Коли ця область обертається навколо$x$ -осі, в результаті виходить тверде тіло з порожниною посередині, а зрізи - шайби. Графік функції і представницької шайби показані на малюнку$\PageIndex{12}$ (а) і (б). Область обертання і отримане тверде тіло показані на малюнку$\PageIndex{12}$ (в) і (г).

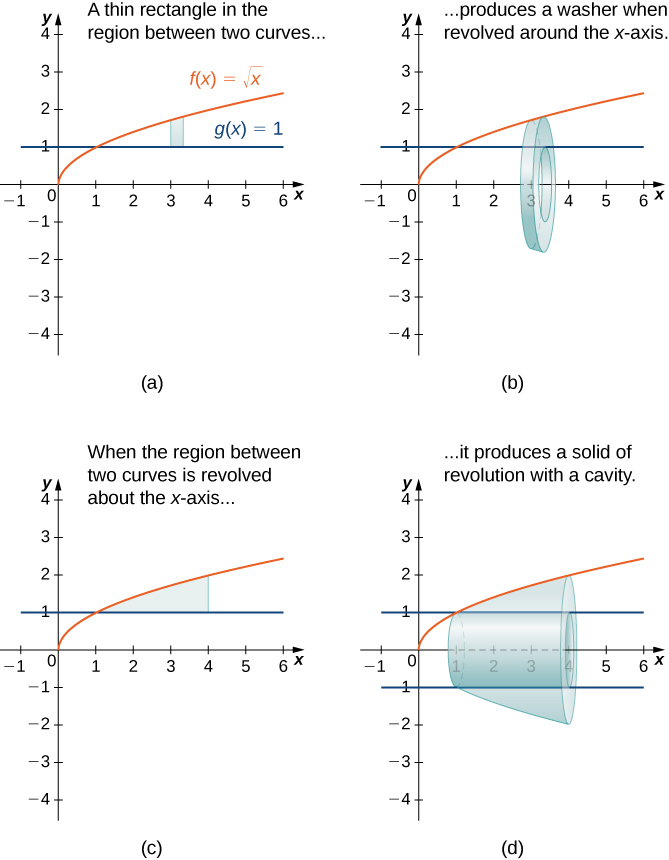
Ця цифра має чотири графіки. Перший граф позначений як «a» і має дві функції f (x) = квадратний корінь (x) і g (x) =1 графіки в першому квадранті. f (x) - це зростаюча крива, що починається з початку, а g (x) - горизонтальна лінія при y = 1. Криві перетинаються на впорядкованій парі (1,1). Між кривими знаходиться затінений прямокутник з нижнім на g (x) і верхнім у f (x). Другий графік з міткою «b» - це ті ж дві криві, що і перший графік. Затінений прямокутник між кривими з першого графіка був повернутий навколо осі x, утворюючи відкритий диск або шайбу. Третій графік з міткою «a» має ті ж дві криві, що і перший графік. Між двома кривими є затінена область між тим, де вони перетинаються, і лінією на x = 4. Четвертий графік - це ті ж дві криві, що і перша з областю з третього графіка, повернутої навколо осі x, утворюючи суцільну область з порожнистим центром. Порожній центр зображено на графіку ламаною горизонтальною лінією на y=1 і y=-1. — Малюнок$\PageIndex{12}$: (а) Тонкий прямокутник в області між двома кривими. (b) Представницький диск, утворений обертанням прямокутника навколо$x$ **-осі.** (c) Область між кривими за заданий інтервал. (г) Отримане тверде тіло революції.

Рисунок$\PageIndex{12}$: (e) Динамічна версія цього твердого тіла обертання, сформована за допомогою CalcPlot3D.

Площа поперечного перерізу, значить, площа зовнішнього кола менше площі внутрішнього кола. У цьому випадку

$A(x)=π\left(\sqrt{x}\right)^2−π(1)^2=π(x−1).$

Тоді обсяг твердого тіла дорівнює

\[V=∫^b_a A(x)\,dx=∫^4_1π(x−1)\,dx=π\left.\left[\frac{x^2}{2}−x\right]\right|^4_1=\frac{9}{2}π\,\text{units}^3. \nonumber \]

Узагальнення цього процесу дає метод шайби.

Правило: Метод шайби

Припустимо,$f(x)$ і$g(x)$ є безперервними, невід'ємними функціями такі, що$f(x)≥g(x)$ над$[a,b]$. Нехай$R$ позначимо область, обмежену вище графіком$f(x)$, нижче на графіку$g(x)$, зліва по лінії$x=a$, а праворуч лінією$x=b$. Потім обсяг твердого тіла обертання, утвореного обертанням$R$ навколо$x$ -осі, задається

\[V=∫^b_aπ\left[(f(x))^2−(g(x))^2\right]\,dx. \nonumber \]

Приклад$\PageIndex{5}$: Using the Washer Method

Знайти об'єм твердого тіла обертання, утвореного обертанням області, обмеженої вище графіком$f(x)=x$ і нижче графіком$g(x)=1/x$ над інтервалом$[1,4]$ навколо$x$ -осі.

Рішення

Графіки функцій і твердого тіла обертання показані на наступному малюнку.

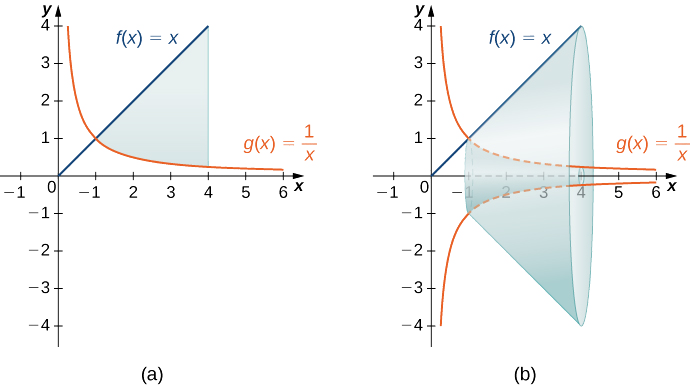
Ця цифра має два графіки. Перший граф позначений як «a» і має дві криві f (x) =x і g (x) =1/x. Вони позначені лише у першому квадранті. f (x) — діагональна лінія, що починається від початку, а g (x) — крива зменшення, вісь y як вертикальна асимптота, а вісь x — горизонтальна асимптота. Графіки перетинаються в (1,1). Між графіками є затінена область, обмежена праворуч лінією в x = 4. Другий графік - це ті ж дві криві. Існує тверде тіло, утворене обертанням затіненої області з першого графіка навколо осі x. — Малюнок$\PageIndex{13}$: (а) Область між графіками функцій$f(x)=x$ і$g(x)=1/x$ над інтервалом$[1,4]$. (b) Обертання області навколо$x$ **-осі** генерує тверду речовину обертання з порожниною посередині.

У нас є

\ [\ begin {align*} V &=^b_aπ\ великий [(f (x)) ^2− (g (x)) ^2\ великий]\, dx=π^4_1\ лівий [x^2−\ лівий (\ frac {1} {x}\ праворуч) ^2\ праворуч]\, dx\\
&= π\ ліворуч. \ ліворуч [\ розрив {x^3} {3} +\ розрив {1} {x}\ праворуч]\ праворуч | ^4_1\
&=\ dfrac {81π} {4}\,\ текст {одиниці} ^3. \ end {вирівнювати*}\]

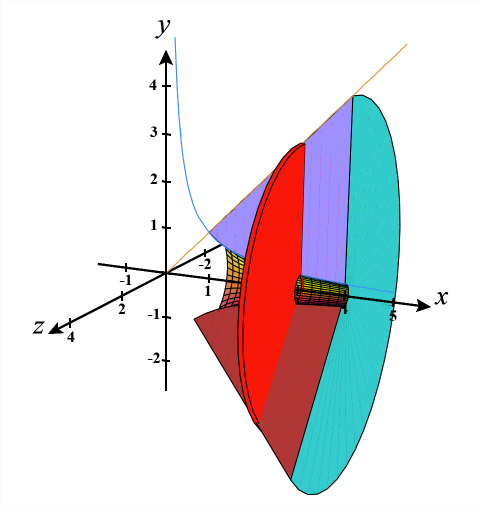
$clipboard_ec285765f5c0a0709a54ba430e31011a6.png$

Рисунок$\PageIndex{13}$: (c) Динамічна версія цього твердого тіла обертання, сформована за допомогою CalcPlot3D.

Вправа$\PageIndex{5}$

Знайти об'єм твердого тіла обертання, утвореного обертанням області, обмеженої графіками$f(x)=\sqrt{x}$ і$g(x)=1/x$ над інтервалом$[1,3]$ навколо $x$-осі.

Підказка: Графік функцій, щоб визначити, який графік утворює верхню межу, а який графік утворює нижню межу, потім скористайтеся процедурою з Прикладу$\PageIndex{5}$.

Відповідь: $\dfrac{10π}{3} \,\text{units}^3$

Як і у випадку з дисковим методом, ми також можемо застосувати метод шайби до твердих тіл обертання, які виникають внаслідок обертання області навколо$y$ осі. В даному випадку діє наступне правило.

Правило: Метод шайби для твердих тіл обертання навколо$y$-axis

Припустимо$u(y)$ і$v(y)$ є безперервними, невід'ємними функціями такі, що$v(y)≤u(y)$ для$y∈[c,d]$. Нехай$Q$ позначають область, обмежену праворуч графіком$u(y)$, зліва на графіку$v(y)$, нижче по лінії$y=c$, а вище по лінії$y=d$. Потім обсяг твердого тіла обертання, утвореного обертанням$Q$ навколо$y$ -осі, задається

\[V=∫^d_cπ\left[(u(y))^2−(v(y))^2\right]\,dy. \nonumber \]

Замість того, щоб дивитися на приклад методу шайби з$y$ -віссю як віссю обертання, ми зараз розглянемо приклад, в якому вісь обертання є лінією, відмінною від однієї з двох координатних осей. Застосовується той же загальний метод, але вам, можливо, доведеться візуалізувати, як описати площу поперечного перерізу обсягу.

Приклад$\PageIndex{6}$:

Знайти об'єм твердого тіла обертання, утвореного обертанням області, обмеженої вище$f(x)=4−x$ і нижче$x$ -віссю через інтервал$[0,4]$ навколо прямої$y=−2.$

Рішення

Графік області і твердого тіла обертання показані на наступному малюнку.

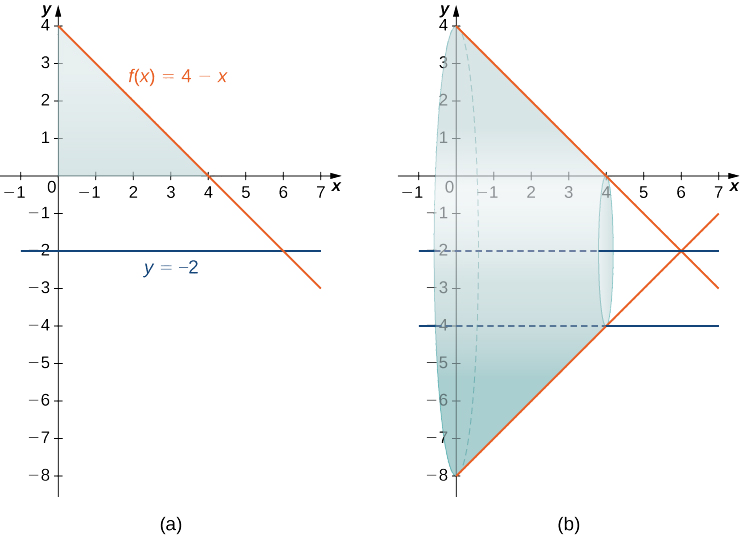
Ця цифра має два графіки. Перший граф має позначення «a» і має дві криві f (x) =4-x та -2. Існує затінена область, яка утворює трикутник, обмежений спадною лінією f (x), віссю y та віссю x. Другий графік - це ті ж дві криві. Існує тверде тіло, утворене обертанням затіненої області з першого графіка навколо лінії y = -2. Усередині твердого тіла є порожнистий циліндр, представлений лініями y=-2 та y = -4. — Рисунок$\PageIndex{14}$: (a) Область між графіком функції$f(x)=4−x$ та **$x$-віссю** над інтервалом$[0,4]$. (b) Обертання області навколо лінії$y=−2$ генерує тверду речовину обертання з циліндричним отвором через його середину.

Ми не можемо застосувати формулу об'єму до цієї задачі безпосередньо, оскільки вісь обертання не є однією з координатних осей. Однак ми ще знаємо, що площа поперечного перерізу - це площа зовнішнього кола менше площі внутрішнього кола. Дивлячись на графік функції, ми бачимо радіус зовнішнього кола, за допомогою$f(x)+2,$ якого спрощує

$f(x)+2=(4−x)+2=6−x.$

Радіус внутрішнього кола$g(x)=2.$ Таким чином, ми маємо

\ [\ почати {вирівнювати*} V &=^4_0π\ ліворуч [(6−x) ^2− (2) ^2\ праворуч]\, dx\\
&= π^4_0 (x^2−12x+32)\, dx=π\ ліворуч. \ ліворуч [\ розрив {x^3} {3} −6x^2+32x\ праворуч]\ праворуч | ^4_0\
&=\ dfrac {160π} {3}\,\ текст {одиниці} ^3. \ end {вирівнювати*}\]

Рисунок$\PageIndex{14}$: (c) Динамічна версія цього твердого тіла обертання, сформована за допомогою CalcPlot3D.

Вправа$\PageIndex{6}$

Знайти об'єм твердого тіла обертання, утвореного обертанням області, обмеженої вище графіком$f(x)=x+2$ і нижче$x$ -віссю через інтервал$[0,3]$ навколо прямої$y=−1.$

Підказка: Скористайтеся процедурою з Прикладу$\PageIndex{6}$.

Відповідь: $60π$одиниць ³

Ключові концепції

Певні інтеграли можуть бути використані для знаходження об'ємів твердих тіл. Використовуючи метод нарізки, ми можемо знайти обсяг, інтегруючи площу поперечного перерізу.
Для твердих тіл обертання об'ємні зрізи часто є дисками, а поперечні перерізи - кола. Метод дисків передбачає застосування методу нарізки в конкретному випадку, в якому перетинами є кола, і використання формули для площі кола.
Якщо тверда речовина обертання має порожнину в центрі, об'ємні зрізи є шайбами. При методі шайб площа внутрішнього кола віднімається з площі зовнішнього кола перед інтеграцією.

Ключові рівняння

Дисковий метод вздовж$x$ -осі

$\displaystyle V=∫^b_aπ\big[f(x)\big]^2\,dx$

Дисковий метод вздовж$y$ -осі

$\displaystyle V=∫^d_cπ\big[g(y)\big]^2\,dy$

Метод шайби

$\displaystyle V=∫^b_aπ\left[(f(x))^2−(g(x))^2\right]\,dx$

Глосарій

поперечний переріз: перетин площини і твердого об'єкта

диск метод: окремий випадок методу нарізки, що використовується з твердими частинами обертання, коли зрізи є дисками

спосіб нарізки: метод розрахунку обсягу твердого тіла, який включає в себе різання твердого тіла на шматки, оцінюючи обсяг кожного шматка, потім додавання цих оцінок, щоб прийти до оцінки загального обсягу; як кількість скибочок йде до нескінченності, ця оцінка стає інтегралом, який дає точне значення обсяг

тверда революція: тверде тіло, що генерується обертається область в площині навколо лінії в цій площині

метод шайби: окремий випадок методу нарізки, що використовується з твердими частинами обертання, коли зрізи є шайбами

Стратегія вирішення проблем: пошук обсягів методом нарізки

Приклад\(\PageIndex{1}\): Deriving the Formula for the Volume of a Pyramid

Вправа\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\): Using the Slicing Method to find the Volume of a Solid of Revolution

Вправа\(\PageIndex{2}\)

Дисковий метод

Приклад\(\PageIndex{3}\): Using the Disk Method to Find the Volume of a Solid of Revolution 1

Вправа\(\PageIndex{3}\)

Правило: Дисковий метод для твердих тіл обертання навколо\(y\)-axis

Приклад\(\PageIndex{4}\): Using the Disk Method to Find the Volume of a Solid of Revolution 2

Вправа\(\PageIndex{4}\)

Правило: Метод шайби

Приклад\(\PageIndex{5}\): Using the Washer Method

Вправа\(\PageIndex{5}\)

Правило: Метод шайби для твердих тіл обертання навколо\(y\)-axis

Приклад\(\PageIndex{6}\):

Вправа\(\PageIndex{6}\)