6.9: Обчислення гіперболічних функцій

Last updated
Save as PDF

Page ID: 61625

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Застосовують формули для похідних та інтегралів гіперболічних функцій.
Застосовують формули для похідних обернених гіперболічних функцій та пов'язаних з ними інтегралів.
Опишіть загальні застосовані умови кутної кривої.

Ми були ознайомлені з гіперболічними функціями раніше, разом з деякими їх основними властивостями. У цьому розділі ми розглянемо формули диференціації та інтеграції гіперболічних функцій та їх обернень.

Похідні та інтеграли гіперболічних функцій

Нагадаємо, що гіперболічний синус і гіперболічний косинус визначаються як

\[\sinh x=\dfrac{e^x−e^{−x}}{2} \nonumber \]

\[\cosh x=\dfrac{e^x+e^{−x}}{2}. \nonumber \]

Інші гіперболічні функції потім визначаються з точки зору\(\sinh x\) і\(\cosh x\). Графіки гіперболічних функцій наведені на рис\(\PageIndex{1}\).

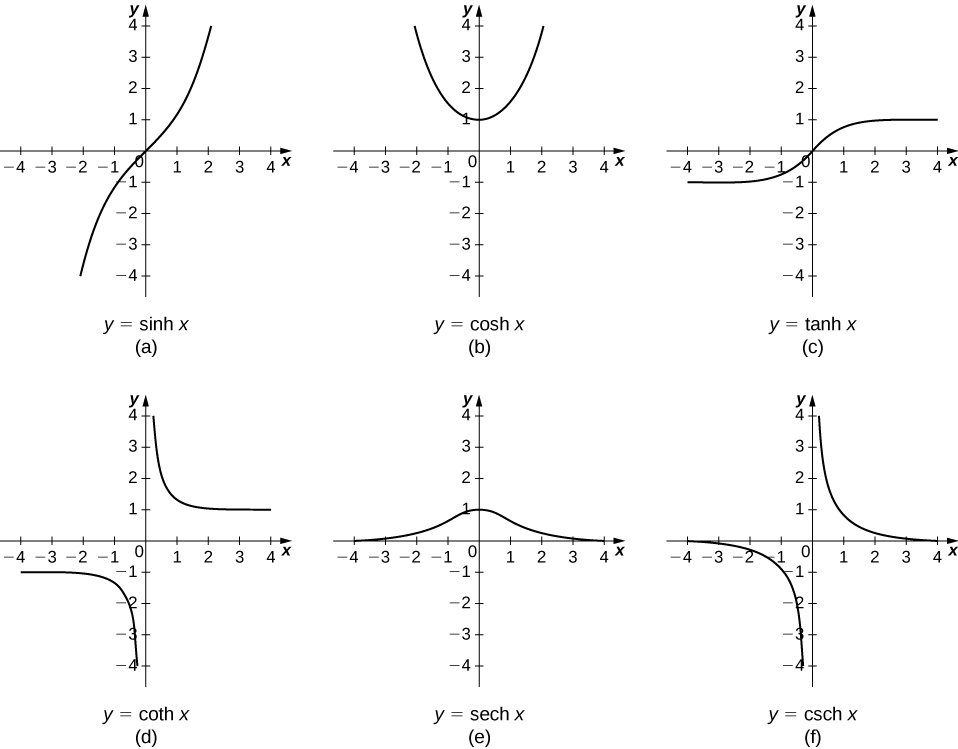
Ця цифра має шість графіків. Перший граф з міткою «a» має функцію y=sinh (x). Це зростаюча функція від 3-го квадранта, через початок до першого квадранта. Другий граф має позначення «b» і має функцію y=cosh (x). Він зменшується у другому квадранті до перехоплення y=1, потім стає зростаючою функцією. Третій граф з міткою «c» має функцію y=tanh (x). Це зростаюча функція від третього квадранта, через початок, до першого квадранта. Четвертий графік має позначення «d» і має функцію y=coth (x). Він має дві частини, один у третьому квадранті та один у першому квадранті з вертикальною асимптотою на осі y. П'ятий граф має позначення «e» і має функцію y=sech (x). Це крива над віссю x, збільшуючись у другому квадранті, до осі y при y = 1, а потім зменшується. Шостий граф має позначення «f» і має функцію y=csch (x). Він має дві частини, один у третьому квадранті та один у першому квадранті з вертикальною асимптотою на осі y. — Малюнок\(\PageIndex{1}\): Графіки гіперболічних функцій.

Легко розробити формули диференціації гіперболічних функцій. Наприклад, дивлячись на\(\sinh x\) нас

\[\begin{align*} \dfrac{d}{dx} \left(\sinh x \right) &=\dfrac{d}{dx} \left(\dfrac{e^x−e^{−x}}{2}\right) \\[4pt] &=\dfrac{1}{2}\left[\dfrac{d}{dx}(e^x)−\dfrac{d}{dx}(e^{−x})\right] \\[4pt] &=\dfrac{1}{2}[e^x+e^{−x}] \\[4pt] &=\cosh x. \end{align*} \nonumber \]

Аналогічно,

\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]

Узагальнено формули диференціювання гіперболічних функцій у табл\(\PageIndex{1}\).

Таблиця\(\PageIndex{1}\): Похідні гіперболічних функцій
\(f(x)\)	\(\dfrac{d}{dx}f(x)\)
\ (f (x)\)» style="вирівнювання тексту: центр; ">\(\sinh x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вирівнювання тексту: центр; ">\(\cosh x\)
\ (f (x)\)» style="вирівнювання тексту: центр; ">\(\cosh x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вирівнювання тексту: центр; ">\(\sinh x\)
\ (f (x)\)» style="вирівнювання тексту: центр; ">\(\tanh x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вирівнювання тексту: центр; ">\(\text{sech}^2 \,x\)
\ (f (x)\)» style="вирівнювання тексту: центр; ">\(\text{coth } x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вирівнювання тексту: центр; ">\(−\text{csch}^2\, x\)
\ (f (x)\)» style="вирівнювання тексту: центр; ">\(\text{sech } x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вирівнювання тексту: центр; ">\(−\text{sech}\, x \tanh x\)
\ (f (x)\)» style="вирівнювання тексту: центр; ">\(\text{csch } x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вирівнювання тексту: центр; ">\(−\text{csch}\, x \coth x\)

Візьмемо хвилинку, щоб порівняти похідні гіперболічних функцій з похідними стандартних тригонометричних функцій. Є багато подібностей, але відмінностей також. Наприклад, збігаються похідні синусоїдальних функцій:

\[\dfrac{d}{dx} \sin x=\cos x \nonumber \]

\[\dfrac{d}{dx} \sinh x=\cosh x. \nonumber \]

Похідні косинусних функцій, однак, розрізняються за знаком:

\[\dfrac{d}{dx} \cos x=−\sin x, \nonumber \]

але

\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]

Продовжуючи вивчення гіперболічних функцій, ми повинні пам'ятати про їх подібність та відмінності зі стандартними тригонометричними функціями. Ці формули диференціації гіперболічних функцій призводять безпосередньо до наступних інтегральних формул.

\[ \begin{align} \int \sinh u \,du &=\cosh u+C \\[4pt] \int \text{csch}^2 u \, du &=−\coth u+C \\[4pt] \int \cosh u \,du &=\sinh u+C \\[4pt] \int \text{sech} \,u \tanh u \,du &=−\text{sech } \,u+C−\text{csch} \,u+C \\[4pt] \int \text{sech }^2u \,du &=\tanh u+C \\[4pt] \int \text{csch} \,u \coth u \,du &=−\text{csch} \,u+C \end{align} \nonumber \]

Приклад\(\PageIndex{1}\): Differentiating Hyperbolic Functions

Оцініть наступні похідні:

\(\dfrac{d}{dx}(\sinh(x^2))\)
\(\dfrac{d}{dx}(\cosh x)^2\)

Рішення:

Використовуючи формули в Таблиці\(\PageIndex{1}\) і правилі ланцюга, отримуємо

\(\dfrac{d}{dx}(\sinh(x^2))=\cosh(x^2)⋅2x\)
\(\dfrac{d}{dx}(\cosh x)^2=2\cosh x\sinh x\)

Вправа\(\PageIndex{1}\)

Оцініть наступні похідні:

\(\dfrac{d}{dx}(\tanh(x^2+3x))\)
\(\dfrac{d}{dx}\left(\dfrac{1}{(\sinh x)^2}\right)\)

Підказка: Використовуйте формули в таблиці\(\PageIndex{1}\) і застосуйте правило ланцюга в міру необхідності.
Відповідь на: \(\dfrac{d}{dx}(\tanh(x^2+3x))=(\text{sech}^2(x^2+3x))(2x+3)\)
Відповідь б: \(\dfrac{d}{dx}\left(\dfrac{1}{(\sinh x)^2}\right)=\dfrac{d}{dx}(\sinh x)^{−2}=−2(\sinh x)^{−3}\cosh x\)

Приклад\(\PageIndex{2}\): Integrals Involving Hyperbolic Functions

Оцініть наступні інтеграли:

\( \displaystyle \int x\cosh(x^2)dx\)
\( \displaystyle \int \tanh x\,dx\)

Рішення

Ми можемо використовувати\(u\) -підстановку в обох випадках.

а. нехай\(u=x^2\). Потім,\(du=2x\,dx\) і

\[\begin{align*} \int x\cosh (x^2)dx &=\int \dfrac{1}{2}\cosh u\,du \\[4pt] &=\dfrac{1}{2}\sinh u+C \\[4pt] &=\dfrac{1}{2}\sinh (x^2)+C. \end{align*}\]

б. нехай\(u=\cosh x\). Потім,\(du=\sinh x\,dx\) і

\[\begin{align*} \int \tanh x \,dx &=\int \dfrac{\sinh x}{\cosh x}\,dx \\[4pt] &=\int \dfrac{1}{u}du \\[4pt] &=\ln|u|+C \\[4pt] &= \ln|\cosh x|+C.\end{align*}\]

Відзначимо, що\(\cosh x>0\) для всіх\(x\), так ми можемо усунути абсолютні значення знаків і отримати

\[\int \tanh x \,dx=\ln(\cosh x)+C. \nonumber \]

Вправа\(\PageIndex{2}\)

Оцініть наступні інтеграли:

\(\displaystyle \int \sinh^3x \cosh x \,dx\)
\(\displaystyle \int \text{sech }^2(3x)\, dx\)

Підказка: Використовуйте наведені вище формули і застосовуйте\(u\) -підстановку в міру необхідності.
Відповідь на: \(\displaystyle \int \sinh^3x \cosh x \,dx=\dfrac{\sinh^4x}{4}+C\)
Відповідь б: \(\displaystyle \int \text{sech }^2(3x) \, dx=\dfrac{\tanh(3x)}{3}+C\)

Обчислення обернених гіперболічних функцій

Дивлячись на графіки гіперболічних функцій, ми бачимо, що при відповідних обмеженнях діапазону всі вони мають зворотні. Більшість необхідних обмежень діапазону можна розгледіти при уважному вивченні графіків. Домени та діапазони обернених гіперболічних функцій зведені в табл\(\PageIndex{2}\).

Таблиця\(\PageIndex{2}\): Домени та діапазони обернених гіперболічних функцій
Функція	Домен	Діапазон
\(\sinh^{−1}x\)	(−∞, ∞)	(−∞, ∞)
\(\cosh^{−1}x\)	(1, ∞)	[0, ∞)
\(\tanh^{−1}x\)	(−1,1)	(−∞, ∞)
\(\coth^{−1}x\)	(−∞, 1) (1, ∞)	(−∞, 0) (0, ∞)
\(\text{sech}^{−1}x\)	(0,1)	[0, ∞)
\(\text{csch}^{−1}x\)	(−∞, 0) (0, ∞)	(−∞, 0) (0, ∞)

Графіки обернених гіперболічних функцій наведені на наступному малюнку.

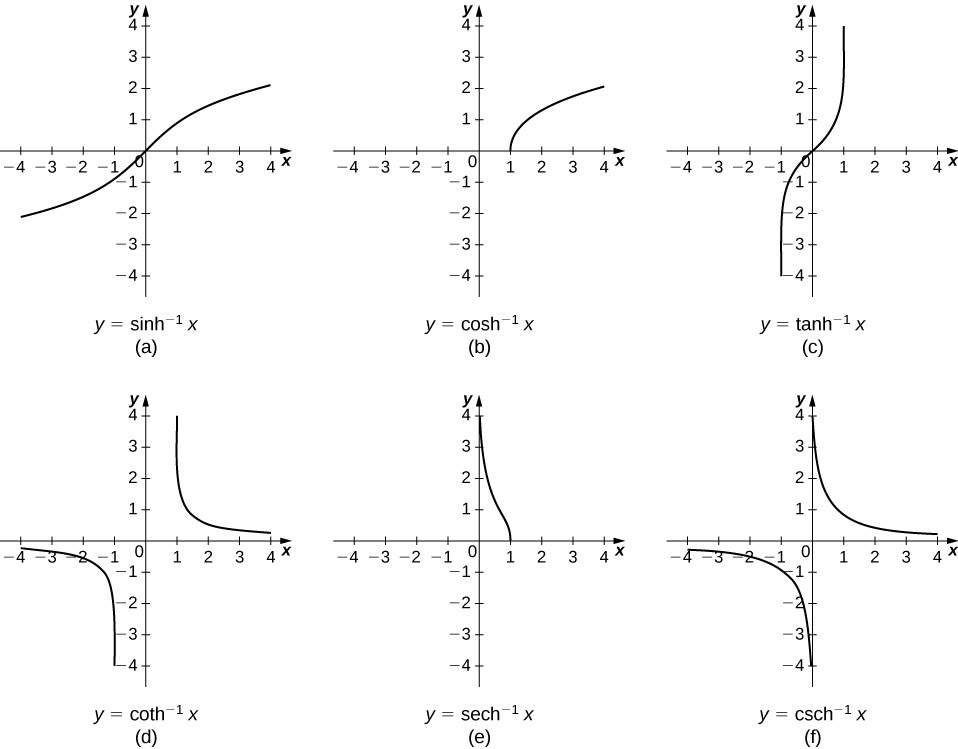
Ця цифра має шість графіків. Перший граф з міткою «a» має функцію y=sinh^-1 (x). Це зростаюча функція від 3-го квадранта, через початок до першого квадранта. Другий граф має позначення «b» і має функцію y=cosh^-1 (x). Він знаходиться в першому квадранті, починаючи на осі х на 2 і збільшуючись. Третій граф з міткою «c» має функцію y=tanh^-1 (x). Це зростаюча функція від третього квадранта, через початок, до першого квадранта. Четвертий граф має позначення «d» і має функцію y=coth^-1 (x). Він має дві частини, один у третьому квадранті та один у першому квадранті з вертикальною асимптотою на осі y. П'ятий граф має позначення «e» і має функцію y=sech^-1 (x). Це крива, що зменшується в першому квадранті і зупиняється на осі x при x = 1. Шостий граф має позначення «f» і має функцію y=csch^-1 (x). Він має дві частини, один у третьому квадранті та один у першому квадранті з вертикальною асимптотою на осі y. — Рисунок\(\PageIndex{3}\): Графіки обернених гіперболічних функцій.

Для знаходження похідних обернених функцій використовується неявна диференціація. У нас є

\[\begin{align} y &=\sinh^{−1}x \\[4pt] \sinh y &=x \\[4pt] \dfrac{d}{dx} \sinh y &=\dfrac{d}{dx}x \\[4pt] \cosh y\dfrac{dy}{dx} &=1. \end{align} \nonumber \]

Нагадаємо, що\(\cosh^2y−\sinh^2y=1,\) так\(\cosh y=\sqrt{1+\sinh^2y}\). Тоді,

\[\dfrac{dy}{dx}=\dfrac{1}{\cosh y}=\dfrac{1}{\sqrt{1+\sinh^2y}}=\dfrac{1}{\sqrt{1+x^2}}. \nonumber \]

Аналогічним чином ми можемо вивести формули диференціації для інших обернених гіперболічних функцій. Ці формули диференціації зведені в табл\(\PageIndex{3}\).

Таблиця\(\PageIndex{3}\): Похідні обернених гіперболічних функцій
\(f(x)\)	\(\dfrac{d}{dx}f(x)\)
\ (f (x)\)» style="вертикальне вирівнювання: середина; ">\(\sinh^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{1}{\sqrt{1+x^2}}\)
\ (f (x)\)» style="вертикальне вирівнювання: середина; ">\(\cosh^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{1}{\sqrt{x^2−1}}\)
\ (f (x)\)» style="вертикальне вирівнювання: середина; ">\(\tanh^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{1}{1−x^2}\)
\ (f (x)\)» style="вертикальне вирівнювання: середина; ">\(\coth^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{1}{1−x^2}\)
\ (f (x)\)» style="вертикальне вирівнювання: середина; ">\(\text{sech}^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{−1}{x\sqrt{1−x^2}}\)
\ (f (x)\)» style="вертикальне вирівнювання: середина; ">\(\text{csch}^{−1}x\)	\ (\ dfrac {d} {dx} f (x)\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{−1}{\|x\|\sqrt{1+x^2}}\)

Зверніть увагу, що\(\coth^{−1}x\) похідні\(\tanh^{−1}x\) і однакові. Таким чином, коли ми інтегруємося\(1/(1−x^2)\), нам потрібно вибрати власне антидериватив на основі області функцій і значень\(x\). Формули інтеграції, що включають обернені гіперболічні функції, узагальнено наступним чином.

\[\int \dfrac{1}{\sqrt{1+u^2}}du=\sinh^{−1}u+C \nonumber \]

\[\int \dfrac{1}{u\sqrt{1−u^2}}du=−\text{sech}^{−1}|u|+C \nonumber \]

\[\int \dfrac{1}{\sqrt{u^2−1}}du=\cosh^{−1}u+C \nonumber \]

\[\int \dfrac{1}{u\sqrt{1+u^2}}du=−\text{csch}^{−1}|u|+C \nonumber \]

\[\int \dfrac{1}{1−u^2}du=\begin{cases}\tanh^{−1}u+C & \text{if }|u|<1\\ \coth^{−1}u+C & \text{if }|u|>1\end{cases} \nonumber \]

Приклад\(\PageIndex{3}\): Differentiating Inverse Hyperbolic Functions

Оцініть наступні похідні:

\(\dfrac{d}{dx}\left(\sinh^{−1}\left(\dfrac{x}{3}\right)\right)\)
\(\dfrac{d}{dx}\left(\tanh^{−1}x\right)^2\)

Рішення

Використовуючи формули в Таблиці\(\PageIndex{3}\) і правилі ланцюга, отримуємо наступні результати:

\(\dfrac{d}{dx}(\sinh^{−1}(\dfrac{x}{3}))=\dfrac{1}{3\sqrt{1+\dfrac{x^2}{9}}}=\dfrac{1}{\sqrt{9+x^2}}\)
\(\dfrac{d}{dx}(\tanh^{−1}x)^2=\dfrac{2(\tanh^{−1}x)}{1−x^2}\)

Вправа\(\PageIndex{3}\)

Оцініть наступні похідні:

\(\dfrac{d}{dx}(\cosh^{−1}(3x))\)
\(\dfrac{d}{dx}(\coth^{−1}x)^3\)

Підказка: Використовуйте формули в таблиці\(\PageIndex{3}\) і застосуйте правило ланцюга в міру необхідності.
Відповідь на: \(\dfrac{d}{dx}(\cosh^{−1}(3x))=\dfrac{3}{\sqrt{9x^2−1}} \)
Відповідь б: \(\dfrac{d}{dx}(\coth^{−1}x)^3=\dfrac{3(\coth^{−1}x)^2}{1−x^2} \)

Приклад\(\PageIndex{4}\): Integrals Involving Inverse Hyperbolic Functions

Оцініть наступні інтеграли:

\(\displaystyle \int \dfrac{1}{\sqrt{4x^2−1}}dx\)
\(\displaystyle \int \dfrac{1}{2x\sqrt{1−9x^2}}dx\)

Рішення

Ми можемо використовувати \(u\)-підстановку в обох випадках.

Нехай\(u=2x\). Тоді,\(du=2\,dx\) і у нас є

\[\begin{align*} \int \dfrac{1}{\sqrt{4x^2−1}}\,dx &=\int \dfrac{1}{2\sqrt{u^2−1}}\,du \\[4pt] &=\dfrac{1}{2}\cosh^{−1}u+C \\[4pt] &=\dfrac{1}{2}\cosh^{−1}(2x)+C. \end{align*} \nonumber \]

Нехай\(u=3x.\) тоді,\(du=3\,dx\) і отримаємо

\[\begin{align*} \int \dfrac{1}{2x\sqrt{1−9x^2}}dx &=\dfrac{1}{2}\int \dfrac{1}{u\sqrt{1−u^2}}du \\[4pt] &=−\dfrac{1}{2}\text{sech}^{−1}|u|+C \\[4pt] &=−\dfrac{1}{2}\text{sech}^{−1}|3x|+C \end{align*}\]

Вправа\(\PageIndex{4}\)

Оцініть наступні інтеграли:

\(\displaystyle \int \dfrac{1}{\sqrt{x^2−4}}dx,x>2\)
\(\displaystyle \int \dfrac{1}{\sqrt{1−e^{2x}}}dx\)

Підказка: Використовуйте наведені вище формули і застосовуйте\(u\) -підстановку в міру необхідності.
Відповідь на: \(\displaystyle \int \dfrac{1}{\sqrt{x^2−4}}dx=\cosh^{−1}(\dfrac{x}{2})+C\)
Відповідь б: \( \displaystyle \int \dfrac{1}{\sqrt{1−e^{2x}}}dx=−\text{sech}^{−1}(e^x)+C\)

Додатки

Одне фізичне застосування гіперболічних функцій передбачає підвішування кабелів. Якщо кабель рівномірної щільності підвішений між двома опорами без будь-якого навантаження, відмінного від власної ваги, кабель утворює криву, звану мережею. Високовольтні лінії електропередач, ланцюги, що звисають між двома стовпами, і нитки павутинної павутини - все це утворюють катенари. На наступному малюнку зображені ланцюга, що звисають з ряду стійок.

Зображення ланцюгів, що висять між стовпами, які приймають форму кутника. — Малюнок\(\PageIndex{3}\): Ланцюги між цими стійками приймають форму кутника. (кредит: модифікація роботи OKFoundryCompany, Flickr)

Гіперболічні функції можуть бути використані для моделювання катенарів. Зокрема, функції форми\(y=a\cdot \cosh(x/a)\) є катенаріями. На малюнку\(\PageIndex{4}\) показаний графік\(y=2\cosh(x/2)\).

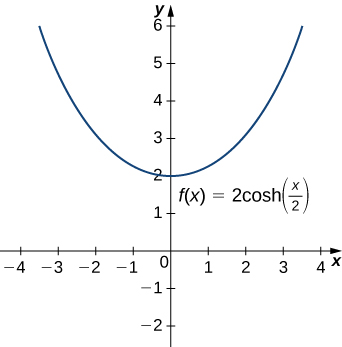
Ця цифра є графіком. Він має функцію f (x) = 2cosh (x/2). Крива зменшується у другому квадранті до осі y. Він перетинає вісь y при y = 2. Потім крива стає все більшою. — Малюнок\(\PageIndex{4}\): Гіперболічна косинусна функція утворює форму кутника.

Приклад\(\PageIndex{5}\): Using a Catenary to Find the Length of a Cable

Припустимо, що підвісний кабель має форму\(10\cosh(x/10)\) для\(−15≤x≤15\), де\(x\) вимірюється в футах. Визначте довжину кабелю (в футах).

Рішення

Нагадаємо з розділу 6.4, що формула для довжини дуги дорівнює

\[\underbrace{\int ^b_a\sqrt{1+[f′(x)]^2}dx}_{\text{Arc Length}}. \nonumber \]

У нас є\(f(x)=10 \cosh(x/10)\), так\(f′(x)=\sinh(x/10)\). Тоді довжина дуги дорівнює

\[\int ^b_a\sqrt{1+[f′(x)]^2}dx=\int ^{15}_{−15}\sqrt{1+\sinh^2 \left(\dfrac{x}{10}\right)}dx. \nonumber \]

Тепер нагадаємо, що

\[1+\sinh^2x=\cosh^2x, \nonumber \]

тому у нас є

\[\begin{align*} \text{Arc Length} &= \int ^{15}_{−15}\sqrt{1+\sinh^2 \left(\dfrac{x}{10}\right)}dx \\[4pt] &=\int ^{15}_{−15}\cosh \left(\dfrac{x}{10}\right)dx \\[4pt] &= \left.10\sinh \left(\dfrac{x}{10}\right)\right|^{15}_{−15}\\[4pt] &=10\left[\sinh\left(\dfrac{3}{2}\right)−\sinh\left(−\dfrac{3}{2}\right)\right]\\[4pt] &=20\sinh \left(\dfrac{3}{2}\right) \\[4pt] &≈42.586\,\text{ft.} \end{align*}\]

Вправа\(\PageIndex{5}\):

Припустимо, що підвісний кабель має форму\(15 \cosh (x/15)\) для\(−20≤x≤20\). Визначте довжину кабелю (в футах).

Відповідь: \(52.95\)футів

Ключові концепції

Гіперболічні функції визначаються термінами експоненціальних функцій.
Построкова диференціація дає формули диференціації гіперболічних функцій. Ці формули диференціації породжують, в свою чергу, інтеграційні формули.
При відповідних обмеженнях діапазону гіперболічні функції мають зворотні.
Неявна диференціація дає формули диференціації обернених гіперболічних функцій, які, в свою чергу, породжують інтеграційні формули.
Найбільш поширеними фізичними додатками гіперболічних функцій є розрахунки за участю катенарів.

Глосарій

катенарний: крива у формі функції\(y=a\cdot\cosh(x/a)\) є мережею; кабель рівномірної щільності, підвішений між двома опорами, приймає форму ланцюга