12.8: Екстремальні значення

Last updated
Save as PDF

Page ID: 60687

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

З огляду на функцію$z=f(x,y)$, нас часто цікавлять точки, де$z$ приймає найбільші або найменші значення. Наприклад, якщо$z$ представляє функцію витрат, ми, швидше за все, хочемо знати, які$(x,y)$ значення мінімізують вартість. Якщо$z$ представляє відношення обсягу до площі поверхні, ми, швидше за все, хотіли б знати,$z$ де найбільше. Це призводить до наступного визначення.

Визначення 97 Відносна і Абсолютна Екстремума

$z=f(x,y)$Дозволяти визначатися на множині,$S$ що містить точку$P=(x_0,y_0)$.

Якщо є відкритий диск, що$D$ містить$P$ таке, що$f(x_0,y_0) \geq f(x,y)$ для всіх$(x,y)$ в$D$, то$f$ має відносний максимум в$P$; якщо$f(x_0,y_0) \leq f(x,y)$ для всіх$(x,y)$ в$D$, то$f$ має відносний мінімум при$P$.
Якщо$f(x_0,y_0)\geq f(x,y)$ для всіх$(x,y)$ в$S$, то$f$ має абсолютний максимум в$P$; якщо$f(x_0,y_0)\leq f(x,y)$ для всіх$(x,y)$ в$S$, то$f$ має абсолютний мінімум при$P$.
Якщо$f$ має відносний максимум або мінімум при$P$, то$f$ має відносну крайність при$P$; якщо$f$ має абсолютний максимум або мінімум при$P$, то$f$ має абсолютну крайність при$P$.

Якщо$f$ має відносний або абсолютний максимум at$P=(x_0,y_0)$, це означає, що кожна крива на поверхні$f$ наскрізного також$P$ матиме відносний або абсолютний максимум при$P$. Згадуючи те, що ми дізналися в розділі 3.1, нахили дотичних ліній до цих кривих$P$ повинні бути 0 або невизначені. Оскільки спрямовані похідні обчислюються за допомогою$f_x$ і$f_y$, ми приводимо до наступного визначення та теореми.

Визначення 98 Критична точка

$z = f(x,y)$Дозволяти бути безперервним на відкритому наборі$S$. Критичною$P=(x_0,y_0)$ точкою$f$ є точка в$S$ такому, що

$f_x(x_0,y_0) = 0$і$f_y(x_0,y_0) = 0$, або
$f_x(x_0,y_0)$і/або$f_y(x_0,y_0)$ не визначено.

Теорема 114 Критичні точки і відносна екстрема

$z=f(x,y)$Дозволяти визначатися на відкритому наборі,$S$ що містить$P=(x_0,y_0)$. Якщо$f$ має відносну крайність при$P$, то$P$ є критичною точкою$f$.

Тому, щоб знайти відносні екстреми, ми знаходимо критичні точки$f$ і визначаємо, які відповідають відносним максимумам, відносним мінімумам або ні ні. Наступні приклади демонструють цей процес.

Приклад$\PageIndex{1}$: Finding critical points and relative extrema

Нехай$f(x,y) = x^2+y^2-xy-x-2$. Знайти відносну крайність$f$.

Рішення

Почнемо з обчислення часткових похідних$f$:

\[f_x(x,y) = 2x-y-1 \qquad \text{and}\qquad f_y(x,y) = 2y-x.\]

Кожен ніколи не є невизначеною. Критична точка виникає, коли$f_x$ і одночасно$f_y$ дорівнює 0, приводячи нас до вирішення наступної системи лінійних рівнянь:

\[2x-y-1 = 0\qquad \text{and}\qquad -x+2y = 0.\]

Це рішення цієї системи є$x=2/3$,$y=1/3$. (Переконайтеся$(2/3,1/3)$, що при,$f_y$ обидва$f_x$ і 0.)

Малюнок 12.27: Поверхня в прикладі 12.8.1 із зазначенням її абсолютного мінімуму.

Графік на малюнку 12.27 показує$f$ разом з цією критичною точкою. З графіка видно, що це відносний мінімум; подальший розгляд функції показує, що це насправді абсолютний мінімум.

Приклад$\PageIndex{2}$: Finding critical points and relative extrema

Нехай$f(x,y) = -\sqrt{x^2+y^2}+2$. Знайти відносну крайність$f$.

Рішення

Почнемо з обчислення часткових похідних$f$:

\[f_x(x,y) = \frac{-x}{\sqrt{x^2+y^2}}\qquad \text{and}\qquad f_y(x,y) = \frac{-y}{\sqrt{x^2+y^2}}.\]

Зрозуміло, що$f_x=0$ коли$x=0$\ &$y\neq0$, і що$f_y=0$ коли$y=0$\ &$x\neq0$. При$(0,0)$, обидва$f_x$ і не$f_y$ є$0$, а скоріше невизначені. Однак ця точка все ще$(0,0)$ є критичною точкою, оскільки часткові похідні не визначені. Це єдина критична точка$f$.

Малюнок 12.28: Поверхня в прикладі 12.8.2 з вказаним абсолютним максимумом.

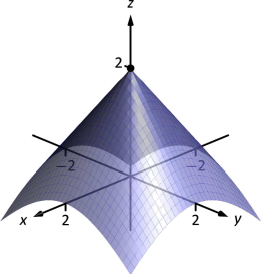
Поверхня$f$ зображена на малюнку 12.28 разом з точкою$(0,0,2)$. Графік показує, що ця точка є абсолютним максимумом$f$.

У кожному з попередніх двох прикладів ми знайшли критичну точку,$f$ а потім визначали, чи є це відносним (або абсолютним) максимумом або мінімумом за допомогою графіків. Було б непогано зуміти визначити, чи відповідає критична точка max або min без графіка. Перш ніж розробити такий тест, ми робимо ще один приклад, який проливає більше світла на питання, які повинен розглянути наш тест.

Приклад$\PageIndex{3}$: Finding critical points and relative extrema

Нехай$f(x,y) = x^3-3x-y^2+4y$. Знайти відносну крайність$f$.

Рішення

Ще раз почнемо з пошуку часткових похідних$f$:

\[f_x(x,y) = 3x^2-3\qquad \text{and} \qquad f_y(x,y) = -2y+4.\]

Кожен завжди визначається. Встановлюючи кожен рівний 0 і вирішуючи для$x$ і$y$, знаходимо

\ [\ begin {align*}
f_x (x, y) = 0\ quad &\ стрілка вправо x =\ pm 1\\
f_y (x, y) = 0\ квад &\ стрілка вправо y = 2.
\ end {вирівнювати*}\]

У нас є дві критичні моменти:$(-1,2)$ і$(1,2)$. Щоб визначити, чи відповідають вони відносному максимуму або мінімуму, розглянемо графік на$f$ малюнку 12.29.

Малюнок 12.29: Поверхня в прикладі 12.8.3 з обома критичними точками позначені.

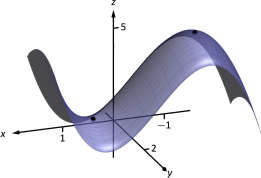
Критична точка$(-1,2)$ чітко відповідає відносному максимуму. Однак критична точка в не$(1,2)$ є ні максимумом, ні мінімумом, відображаючи іншу, цікаву характеристику.

Якщо йти паралельно$y$ -осі до цієї критичної точки, то ця точка стає відносним максимумом на цьому шляху. Але якщо йти до цієї точки паралельно$x$ -осі, ця точка стає відносним мінімумом уздовж цього шляху. Точка, яка, здається, діє як макс, так і хв, - це точка сідла. Далі слід формальне визначення.

Визначення 99 Точка сідла

$P=(x_0,y_0)$Дозволяти бути в області$f$ де$f_x=0$ і$f_y=0$ в$P$. $P$є сідловою точкою$f$ якщо, для кожного відкритого диска$P$,$D$ що містить, є точки$(x_1,y_1)$ і$(x_2,y_2)$ в$D$ таких, що$f(x_0,y_0)>f(x_1,y_1)$ і$f(x_0,y_0)<f(x_2,y_2)$.

У точці сідла миттєва швидкість зміни у всіх напрямках дорівнює 0 і є точки поблизу з$z$ -значеннями як менше, так і більше$z$ -значення точки сідла.

Перед прикладом 12.8.3 ми згадували про необхідність тесту для розмежування відносних максимумів і мінімумів. Тепер ми визнаємо, що наш тест також повинен враховувати точки сідла. Для цього розглянемо другі часткові похідні від$f$.

Нагадаємо, що з одинарними змінними функціями$y=f(x)$, такими як$f''(c)>0$, якщо,$f$ то увігнута вгору в$c$, а якщо$f'(c) =0$, то$f$ має відносний мінімум при$x=c$. (Ми назвали це другим похідним тестом.) Зверніть увагу, що в точці сідла здається, що графік «обидва» увігнуті вгору і увігнуті вниз, залежно від того, який напрямок ви розглядаєте.

Було б непогано, якби вірно було наступне:

$12.8 words.PNG$

Однак це не так. Функції$f$ існують там, де$f_{xx}$ і$f_{yy}$ є позитивними, але точка сідла все ще існує. У такому випадку, поки увігнутість в$x$ -напрямку вгору (тобто$f_{xx}>0$), а увігнутість в$y$ -напрямку також вгору (тобто$f_{yy}>0$), увігнутість перемикається десь між$x$ - і$y$ -напрямками.

Щоб врахувати це, розглянемо$D = f_{xx}f_{yy}-f_{xy}f_{yx}$. Оскільки$f_{xy}$ і рівні$f_{yx}$, коли безперервні (поверніться до теореми 103), ми можемо переписати це як$D = f_{xx}f_{yy}-f_{xy}^{\,2}$. $D$може використовуватися для перевірки того, чи змінюється увігнутість у точці залежно від напрямку. Якщо$D>0$, увігнутість не перемикається (тобто в цій точці графік увігнутий вгору або вниз у всіх напрямках). Якщо$D<0$, увігнутість дійсно перемикається. Якщо$D=0$, наш тест не зможе визначити, вимикається увігнутість чи ні. Ми констатуємо використання$D$ в наступній теоремі.

ТЕОРЕМА 115 Другий тест на похідну

$z=f(x,y)$Дозволяти диференціюватися на відкритому множині$P = (x_0,y_0)$, що містить, і нехай
\[D = f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)-f_{xy}^{\,2}(x_0,y_0).\]

Якщо$D>0$ і$f_{xx}(x_0,y_0)>0$,$P$ то відносний мінімум$f$.
Якщо$D>0$ і$f_{xx}(x_0,y_0)<0$,$P$ то відносний максимум$f$.
Якщо$D<0$, то$P$ є сідловою точкою$f$.
Якщо$D=0$, тест непереконливий.

Ми спочатку практикуємося використовувати цей тест з функцією в попередньому прикладі, де ми візуально визначили, що у нас є відносний максимум і точка сідла.

Приклад$\PageIndex{4}$: Using the Second Derivative Test

Нехай$f(x,y) = x^3-3x-y^2+4y$ як у прикладі 12.8.3. Визначте, чи має функція відносну мінімальну, максимальну або сідлову точку в кожній критичній точці.

Рішення
Ми визначили раніше, що критичними точками$f$ є$(-1,2)$ і$(1,2)$. Щоб використовувати другий тест похідних, ми повинні знайти другі часткові похідні$f$:
\[f_{xx} = 6x;\qquad f_{yy} = -2;\qquad f_{xy} = 0.\]
Таким чином$D(x,y) = -12x$.

За адресою$(-1,2)$:$D(-1,2) = 12>0$, і$f_{xx}(-1,2) = -6$. За Другим похідним тестом,$f$ має відносний максимум при$(-1,2)$.

За адресою$(1,2)$:$D(1,2) = -12 <0$. Другий тест похідних стверджує, що$f$ має точку сідла в$(1,2)$.

Другий тест похідних підтвердив те, що ми визначили візуально.

Приклад$\PageIndex{5}$: Using the Second Derivative Test

Знайти відносну крайність$f(x,y) = x^2y+y^2+xy$.

Рішення

Почнемо з знаходження першого і другого часткових похідних$f$:

\ [\ почати {масив} {ccc}
f_x = 2xy+y & f_y = x^2+2y+x\\
f_ {xx} = 2y & f_ {yy} = 2\\ f_ {xy} = 2x+1 &
f_ {yx} = 2х+1 & f_ {yx} = 2x+1.
\ end {масив}\]

Ми знаходимо критичні точки, знаходячи де$f_x$ і$f_y$ одночасно 0 (вони обидва ніколи не визначені). Налаштування$f_x=0$, у нас є:

\[f_x=0 \quad \Rightarrow \quad 2xy+y=0\quad \Rightarrow \quad y(2x+1)=0.\]

Це означає, що для$f_x=0$, або$y=0$ або$2x+1=0$.

Припустимо$y=0$, тоді розглянемо$f_y=0$:

\ [\ begin {align*}
f_y &= 0\\
x^2y+x &= 0,\ qquad\ text {і оскільки$y=0$, ми маємо}\\
x^2+x &= 0\\
x (x+1) & = 0.
\ end {вирівнювати*}\]

Таким чином$y=0$, якщо, у нас є$x=0$ або$x=-1$, даючи дві критичні точки:$(-1,0)$ і$(0,0)$.

Повертаючись до$f_x$, тепер припустимо$2x+1=0$, тобто, що$x=-1/2$, потім розглянемо$f_y=0$:

\ [\ begin {align*}
f_y &= 0\\
x^2y+x &= 0,\ qquad\ text {і оскільки$x=-1/2$ ми маємо}\\
1/4+2y-1/2 &= 0\\
y&= 1/8.
\ end {вирівнювати*}\]

Таким чином$x=-1/2$, якщо,$y=1/8$ даючи критичну точку$(-1/2,1/8)$.

З$D = 4y-(2x+1)^2$, ми застосовуємо Другий тест похідних до кожної критичної точки.

В$(-1,0)$$D <0$, так$(-1,0)$ це точка сідла.

В$(0,0)$$D<0$, так само$(0,0)$ є і сідлової точкою.

В$(-1/2,1/8)$,$D>0$ і$f_{xx} > 0$, так$(-1/2,1/8)$ це відносний мінімум.

Малюнок 12.30: Графік$f$ із прикладу 12.8.5 та його відносна крайність.

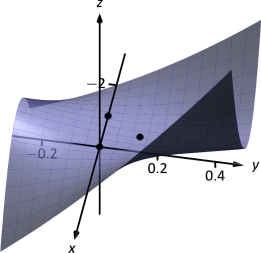
На малюнку 12.30 показаний графік$f$ і три критичні точки. Зверніть увагу, як ця функція не сильно змінюється поблизу критичних точок — тобто візуально важко визначити, чи є точка точкою сідла або відносним мінімумом (або навіть критичною точкою взагалі!). Це одна з причин, чому другий похідний тест так важливо мати.

Обмежена оптимізація

При оптимізації функцій однієї змінної, таких як$y=f(x)$, ми використовували теорему 25, теорему екстремальних значень, яка говорила, що протягом замкнутого інтервалу безперервна функція має як максимальне$I$, так і мінімальне значення. Щоб знайти ці максимальні і мінімальні значення, ми оцінили$f$ у всіх критичних точках інтервалу, а також в кінцевих точках («кордоні») інтервалу.

Аналогічна теорема і процедура застосовується до функцій двох змінних. Неперервна функція над замкнутою множиною також досягає максимального та мінімального значення (див. наступну теорему). Ми можемо знайти ці значення, оцінюючи функцію при критичних значеннях у множині та за межами множини. Після формального викладання цієї теореми про крайні значення наведемо приклади.

Теорема 116 Теорема про екстремальні значення

$z=f(x,y)$Дозволяти бути безперервна функція на замкнутому обмеженому множині$S$. Потім$f$ має максимальне і мінімальне значення на$S$.

Приклад$\PageIndex{6}$: Finding extrema on a closed set

Дозволяти$f(x,y) = x^2-y^2+5$ і$S$ нехай трикутник з вершинами$(-1,-2)$,$(0,1)$ і$(2,-2)$. Знайти максимальне і мінімальне значення$f$ включення$S$.

Рішення
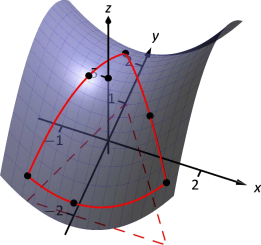
Це може допомогти побачити графік$f$ разом з безліччю$S$. На малюнку 12.31 (a) визначення трикутника$S$ показано у$xy$ -площині пунктирною лінією. Над нею знаходиться поверхня$f$; нас стосується лише частина,$f$ укладена «трикутником» на його поверхні.

Малюнок 12.31: Побудова поверхні$f$ разом з обмеженим доменом S.

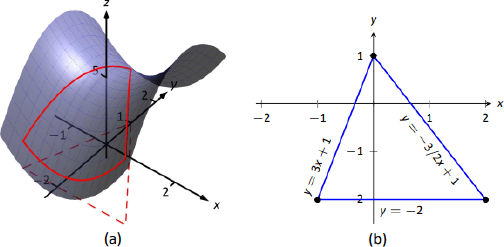
Починаємо з пошуку критичних точок$f$. З$f_x = 2x$ і$f_y = -2y$, знаходимо тільки одну критичну точку, в$(0,0)$.

Тепер знайдемо максимальне і мінімальне значення,$f$ які досягають уздовж кордону$S$, тобто по краях трикутника. На малюнку 12.31 (б) ми бачимо накиданий в площині трикутник з рівняннями ліній, що утворюють його краї з маркуванням.

Почніть з нижнього краю, по лінії$y=-2$. Якщо$y$ є$-2$, то на поверхні ми розглядаємо точки$f(x,-2)$; тобто наша функція зводиться до$f(x,-2) = x^2-(-2)^2+5 = x^2+1=f_1(x)$. Ми хочемо максимізувати/мінімізувати$f_1(x)=x^2+1$ на інтервалі$[-1,2]$. Для цього ми оцінюємо$f_1(x)$ в критичних точках і в кінцевих точках.

Критичні точки$f_1$ знаходять шляхом встановлення її похідної рівною 0:
\[f'_1(x)=0\qquad \Rightarrow x=0.\]
Оцінювання$f_1$ в цій критичній точці, а в кінцевих точках$[-1,2]$ дає:
\ [\ begin {align*}
f_1 (-1) = 2\ qquad&\ Rightarrow\ qquad f (-1, -2) = 2\\
f_1 (0) = 1\ qquad&\ Стрілка вправо\ квадрат f (0, -2) = 1\\
f_1 (2) = 5\ qquad&\ Стрілка вправо\ квадрат f (2, -2) = 5.
\ end {align*}\]
Зауважте, як оцінка$f_1$ в точці збігається з оцінкою$f$ у відповідній точці.

Нам потрібно зробити цей процес в два рази більше, для двох інших країв трикутника.

Уздовж лівого краю, по лінії$y=3x+1$, підставляємо$3x+1$ в для$y$ in$f(x,y)$:
\[f(x,y) = f(x,3x+1) = x^2-(3x+1)^2+5 = -8x^2-6x+4 = f_2(x).\]
Ми хочемо максимальне і мінімальне значення$f_2$ на інтервалі$[-1,0]$, тому оцінюємо$f_2$ в його критичних точках і кінцевих точках інтервал. Знаходимо критичні точки:
\[f'_2(x) = -16x-6=0 \qquad \Rightarrow \qquad x=-3/8.\]

Оцінити$f_2$ в його критичній точці та кінцевих точках$[-1,0]$:
\ [\ begin {align*}
f_2 (-1) = 2\ qquad&\ Rightarrow\ qquad f (-1, -2) = 2\\
f_2 (-3/8) = 41/8=5,125\ qquad&\ Rightarrow\ qquad f (-3/8, -0.125) = 5,125\
f_2 (0) = 1\ квадратний&\ стрілка вправо\ квадрат f (0,1) = 4.
\ end {вирівнювати*}\]

Нарешті, оцінюємо$f$ уздовж правого краю трикутника, де$y = -3/2x+1$.
\[f(x,y) = f(x,-3/2x+1) = x^2-(-3/2x+1)^2+5 = -\frac54x^2+3x+4=f_3(x).\]
Критичні точки:$f_3(x)$ Ми
\[f'_3(x) = 0 \qquad \Rightarrow \qquad x=6/5=1.2.\]
оцінюємо$f_3$ в цій критичній точці і в кінцевих точках інтервалу$[0,2]$:
\ [\ begin {align*}
f_3 (0) = 4\ qquad&\ Rightarrow\ qquad f (0,1) = 4\\
f_3 (1,2) = 5.8\ qquad&\ Стрілка вправо\ квадрат f (1,2, -0,8) = 5,8\\
f_3 (2) = 5\ qquad&\\ Стрілка вправо\ квадрат f (2, -2) = 5.
\ end {align*}\]
Остання точка для перевірки: критична точка$f$,$(0,0)$. Знаходимо$f(0,0) = 5$.

Малюнок 12.32: Поверхня$f$ поряд з важливими точками вздовж кордону S і внутрішньої частини.

Ми оцінили$f$ в цілому 7 різних місць, все це показано на малюнку 12.32. Ми перевірили кожну вершину трикутника двічі, оскільки кожна виявилася кінцевою точкою інтервалу двічі. З усіх$z$ знайдених -значень максимальне дорівнює 5,8, знайдено при$(1.2,-0.8)$; мінімальне - 1, знайдено в$(0,-2)$.

Ця частина тексту має назву «Обмежена оптимізація», оскільки ми хочемо оптимізувати функцію (тобто знайти її максимальні та/або мінімальні значення) з урахуванням обмежень — обмежень, на які розглядаються вхідні точки. У попередньому прикладі ми обмежилися, розглядаючи функцію тільки в межах трикутника. Це було багато в чому довільно; функція і межа були обрані просто як приклад, без реального «значення» за функцією або обраним обмеженням.

Однак вирішення обмежених задач оптимізації є дуже важливою темою в прикладній математиці. Розроблені тут методики є основою для вирішення більших задач, де задіяно більше двох змінних.

Проілюструємо техніку ще раз класичною задачею.

Приклад$\PageIndex{7}$: Constrained Optimization

Поштова служба США стверджує, що обхват+довжина стандартного поштового пакету не повинна перевищувати 130». З огляду на прямокутну коробку, «довжина» - найдовша сторона, а «обхват» в два рази більше ширини+висота.

Враховуючи прямокутну коробку, де ширина та висота рівні, які розміри коробки надають максимальний обсяг за умови обмеження розміру стандартного поштового пакету?

Рішення

Нехай$w$,$h$ і$\ell$ позначають ширину, висоту і довжину прямокутної коробки; ми припускаємо тут, що$w=h$. Обхват тоді$2(w+h) = 4w$. Обсяг коробки дорівнює$V(w,\ell) = wh\ell = w^2\ell$. Бажаємо максимізувати цей обсяг за умови обмеження$4w+\ell\leq 130$, або$\ell\leq 130-4w$. (Здоровий глузд також вказує на це$\ell>0, w>0$.)

Почнемо з знаходження критичних значень$V$. Ми знаходимо, що$V_w = 2w\ell$ і$V_\ell = w^2$; вони одночасно 0 тільки в$(0,0)$. Це дає обсяг 0, тому ми можемо ігнорувати цю критичну точку.

Тепер розглянемо обсяг по обмеженню$\ell=130-4w.$ Уздовж цієї лінії у нас є:
\[V(w,\ell) = V(w,130-4w) = w^2(130-4w) = 130w^2-4w^3 = V_1(w).\]
Обмеження застосовується на$w$ -інтервалі,$[0,32.5]$ як зазначено на малюнку. Таким чином, ми хочемо максимізувати$V_1$$[0,32.5]$.

Знайшовши критичні значення$V_1$, беремо похідну і ставимо її рівною 0:
\[V\,'_1(w) = 260w-12w^2 = 0 \quad \Rightarrow \quad w(260-12w)= 0 \quad \Rightarrow \quad w=0,\frac{260}{12}\approx 21.67.\]

Ми знайшли два критичних значення: коли$w=0$ і коли$w=21.67$. Ми знову ігноруємо$w=0$ рішення; максимальний обсяг, за умови обмеження, приходить на$w=h=21.67$,$\ell = 130-4(21.6) =43.33.$ Це дає обсяг$V(21.67,43.33) \approx 19,408$ в$^3$.

Малюнок 12.33: Графік об'єму коробки з обхватом 4w та довжиною$l$, за умови обмеження розміру.

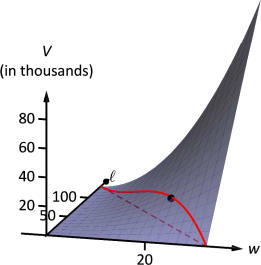
Функція гучності$V(w,\ell)$ показана на малюнку 12.33 разом з обмеженням$\ell = 130-4w$. Як і раніше, обмеження малюється пунктирним у$xy$ -площині, а також вздовж поверхні функції. Позначається точка, де обсяг максимізується.

Важко переоцінити важливість оптимізації. У «реальному світі» ми зазвичай прагнемо зробити щось краще. Висловлюючи щось як математичну функцію, «зробити щось краще» означає «оптимізувати якусь функцію».

Методи, показані тут, є лише початком неймовірно важливого поля. Багато функцій, які ми прагнемо оптимізувати, неймовірно складні, що робить крок «знайти градієнт і встановити його рівним$\vec 0$" вельми нетривіальним. Оволодіння принципами тут є ключовим для того, щоб мати можливість вирішити ці більш складні проблеми.

Дописувачі та авторства

Template:ContribApexCalc