6.1: Області між кривими

Last updated
Save as PDF

Page ID: 61737

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте площу області між двома кривими шляхом інтеграції щодо незалежної змінної.
Знайдіть площу складеної області.
Визначте площу області між двома кривими шляхом інтеграції щодо залежної змінної.

У Вступі до інтеграції ми розробили концепцію певного інтеграла для обчислення площі під кривою на заданому інтервалі. У цьому розділі ми розширюємо цю ідею, щоб обчислити площу більш складних регіонів. Ми почнемо з пошуку області між двома кривими, які є функціями$\displaystyle x$, починаючи з простого випадку, в якому значення однієї функції завжди більше іншого. Потім ми розглянемо випадки, коли графіки функцій перетинаються. В останню чергу ми розглянемо, як обчислити площу між двома кривими, які є функціями$\displaystyle y$.

Площа області між двома кривими

$\displaystyle f(x)$$\displaystyle g(x)$Дозволяти і бути безперервні функції протягом інтервалу$\displaystyle [a,b]$ такі, що$\displaystyle f(x)≥g(x)$ на$\displaystyle [a,b]$. Ми хочемо знайти площу між графіками функцій, як показано на малюнку$\PageIndex{1}$.

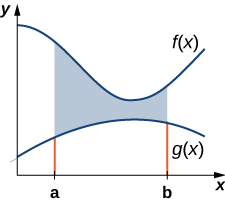
Ця цифра являє собою графік в першому квадранті. На графіку є дві криві. Вища крива позначається як «f (x)», а нижня крива - «g (x)». На осі x є дві межі, позначені a та b. Між двома кривими є затінена область, обмежена лініями на x = a та x=b. — Малюнок$\PageIndex{1}$: Площа між графами двох функцій,$\displaystyle f(x)$ і$\displaystyle g(x)$, на інтервалі$\displaystyle [a,b]$

Як ми робили раніше, ми збираємося розділити інтервал на осі х і наблизити площу між графіками функцій прямокутниками. Отже, для$\displaystyle i=0,1,2,…,n$, нехай$\displaystyle P={x_i}$ буде звичайна перегородка$\displaystyle [a,b]$. Потім, для$\displaystyle i=1,2,…,n,$ вибираємо точку$\displaystyle x^∗_i∈[x_{i−1},x_i]$, і на кожному інтервалі$\displaystyle [x_{i−1},x_i]$ будуємо прямокутник, який простягається вертикально від$\displaystyle g(x^∗_i)$ до$\displaystyle f(x^∗_i)$. $\PageIndex{2a}$На малюнку показані прямокутники, коли$\displaystyle x^∗_i$ вибрано ліву кінцеву точку інтервалу і$\displaystyle n=10$. $\PageIndex{2b}$На малюнку детально зображений представницький прямокутник.

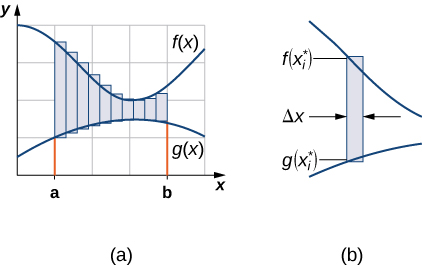
Ця цифра має три графіки. Перший графік має дві криві, одна над іншою. У проміжках між кривими знаходиться прямокутник. Вершина прямокутника знаходиться на верхній кривій з позначкою «f (x*)», а нижня частина прямокутника - на нижній кривій і позначена «g (x*)». Другий графік, позначений «(a)», має дві криві на графіку. Вища крива позначається як «f (x)», а нижня крива - «g (x)». На осі x є дві межі, позначені a і b. Між двома кривими є затінена область, обмежена лініями у x = a і x=b. Третій граф з міткою «(b)» має дві криві одна над іншою. Перша крива позначена «f (x*)», а нижня крива позначена «g (x*)». Між ними є затінений прямокутник. Ширина прямокутника позначається як «delta x». — Малюнок$\PageIndex{2}$: (а) Ми можемо наблизити площу між графіками двох функцій,$\displaystyle f(x)$ причому$\displaystyle g(x)$, з прямокутниками. (b) Площа типового прямокутника переходить від однієї кривої до іншої.

Висота кожного окремого прямокутника дорівнює$\displaystyle f(x^∗_i)−g(x^∗_i)$ і ширина кожного прямокутника дорівнює$\displaystyle Δx$. Складаючи області всіх прямокутників, ми бачимо, що площа між кривими наближена

\[\displaystyle A≈\sum_{i=1}^n[f(x^∗_i)−g(x^∗_i)]Δx. \nonumber \]

Це сума Рімана, тому ми беремо ліміт як$\displaystyle n→∞$ і отримуємо

\[\displaystyle A=\lim_{n→∞}\sum_{i=1}^n[f(x^∗_i)−g(x^∗_i)]Δx=\int ^b_a[f(x)−g(x)]dx. \nonumber \]

Ці висновки узагальнені в наступній теоремі.

Пошук області між двома кривими

$\displaystyle f(x)$$\displaystyle g(x)$Дозволяти і бути безперервні функції такі, що$\displaystyle f(x)≥g(x)$ протягом інтервалу [$\displaystyle a,b]$. Нехай R позначають область, обмежену вище графіком$\displaystyle f(x)$, нижче графіком$\displaystyle g(x)$, а зліва і справа лініями$\displaystyle x=a$ і$\displaystyle x=b$, відповідно. Потім площа$\textbf{R}$ задається

\[A=\int ^b_a[f(x)−g(x)]dx. \nonumber \]

Ми застосуємо цю теорему в наступному прикладі.

Приклад$\PageIndex{1}$: Finding the Area of a Region between Two Curves I

Якщо$\textbf{R}$ область обмежена вище графіком функції$\displaystyle f(x)=x+4$ і нижче графіком функції$\displaystyle g(x)=3−\dfrac{x}{2}$ за інтервалом$\displaystyle [1,4]$, знайдіть площу області$\textbf{R}$.

Рішення

Регіон зображений на наступному малюнку.

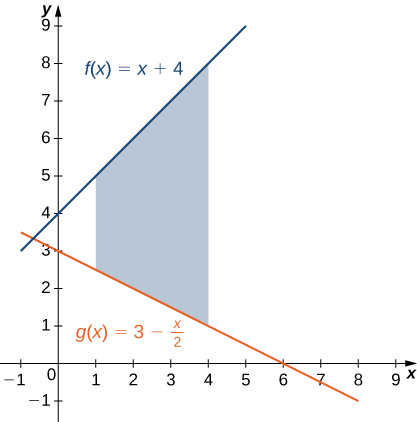
Ця цифра має два лінійних графіка в першому квадранті. Ними є функції f (x) = x+4 і g (x) = 3-x/2. Між цими рядками знаходиться затінена область, обмежена вище f (x) і нижче g (x). Затінена область знаходиться між x=1 і x=4. — Малюнок$\PageIndex{3}$: Показується область між двома кривими, де одна крива завжди більша за іншу.

У нас є

\[ \begin{align*} A =\int ^b_a[f(x)−g(x)]\,dx \\[4pt] =\int ^4_1[(x+4)−(3−\dfrac{x}{2})]\,dx=\int ^4_1\left[\dfrac{3x}{2}+1\right]\,dx \\[4pt] =[\dfrac{3x^2}{4}+x]\bigg|^4_1=(16−\dfrac{7}{4})=\dfrac{57}{4}. \end{align*}\]

Площа області - це$\displaystyle \dfrac{57}{4}units^2$.

Вправа$\PageIndex{1}$

Якщо$\textbf{R}$ область обмежена графіками функцій$\displaystyle f(x)=\dfrac{x}{2}+5$ і$\displaystyle g(x)=x+\dfrac{1}{2}$ над інтервалом$\displaystyle [1,5]$, знайдіть площу області$\textbf{R}$.

Підказка: Графік функцій, щоб визначити графік якої функції утворює верхню межу, а яка утворює нижню межу, а потім виконайте процес, який використовується в Прикладі.

Відповідь: $\displaystyle 12$одиниць ²

У прикладі$\PageIndex{1}$ ми визначили інтервал інтересу як частину постановки задачі. Досить часто, однак, ми хочемо визначити наш інтервал інтересу на основі того, де графіки двох функцій перетинаються. Це проілюстровано на наступному прикладі.

Приклад$\PageIndex{2}$: Finding the Area of a Region between Two Curves II

Якщо$\textbf{R}$ область обмежена вище графіком функції$\displaystyle f(x)=9−(x/2)^2$ і нижче графіком функції$\displaystyle g(x)=6−x$, знайдіть область області$\textbf{R}$.

Рішення

Регіон зображений на наступному малюнку.

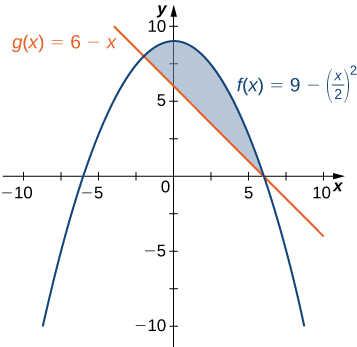
Ця цифра має два графіки в першому квадранті. Ними є функції f (x) = 9- (x/2) ^2 і g (x) = 6-х. Між цими графіками перевернута парабола і лінія - це затінена область, обмежена вище f (x) і нижче g (x). — Малюнок$\PageIndex{4}$: Цей графік показує область під графіком$\displaystyle f(x)$ і вище графіка$\displaystyle g(x).$

Спочатку потрібно обчислити, де перетинаються графіки функцій. Налаштування$\displaystyle f(x)=g(x),$ отримуємо

\[ \begin{align*} \displaystyle f(x) =g(x) \\[4pt] 9−(\dfrac{x}{2})^2 =6−x\\[4pt] 9−\dfrac{x^2}{4} =6−x\\[4pt] 36−x^2 =24−4x\\[4pt] x^2−4x−12 =0\\[4pt] (x−6)(x+2) =0. \end{align*}\]

Графіки функцій перетинаються, коли$\displaystyle x=6$ або близько$\displaystyle x=−2,$ того ми хочемо інтегрувати від$\displaystyle −2$ до$\displaystyle 6$. Так як$\displaystyle f(x)≥g(x)$ за$\displaystyle −2≤x≤6,$ ми отримуємо

\[\begin{align*} \displaystyle A =\int ^b_a[f(x)−g(x)]\,dx \\ =\int ^6_{−2} \left[9−(\dfrac{x}{2})^2−(6−x)\right]\,dx \\ =\int ^6_{−2}\left[3−\dfrac{x^2}{4}+x\right]\,dx \\ = \left. \left[3x−\dfrac{x^3}{12}+\dfrac{x^2}{2}\right] \right|^6_{−2}=\dfrac{64}{3}. \end{align*}\]

Площа області -$\displaystyle 64/3$ одиниці ².

Вправа$\PageIndex{2}$

Якщо$\textbf{R}$ область обмежена вище графіком функції$\displaystyle f(x)=x$ і нижче графіком функції$\displaystyle g(x)=x^4$, знайдіть область області$\textbf{R}$.

Підказка: Скористайтеся процесом з Прикладу$\PageIndex{2}$.

Відповідь: $\displaystyle \dfrac{3}{10}$блок ²

Області складних регіонів

Поки що ми вимагали$\displaystyle f(x)≥g(x)$ протягом усього інтервалу інтересу, але що робити, якщо ми хочемо подивитися на регіони, обмежені графіками функцій, які перетинають один одного? У цьому випадку ми модифікуємо процес, який ми тільки що розробили, використовуючи функцію абсолютного значення.

Пошук площі області між кривими, що перетинаються

$\displaystyle g(x)$Дозволяти$\displaystyle f(x)$ і бути безперервними функціями протягом інтервалу$\displaystyle [a,b]$. Нехай$\textbf{R}$ позначають область між графами$\displaystyle f(x)$ і$\displaystyle g(x)$, і бути обмежені зліва і справа лініями$\displaystyle x=a$ і$\displaystyle x=b$, відповідно. Потім площа$\textbf{R}$ задається

\[A=\int ^b_a|f(x)−g(x)|dx. \nonumber \]

На практиці застосування цієї теореми вимагає від нас розбити інтервал$\displaystyle [a,b]$ і оцінити кілька інтегралів, в залежності від того, яке з значень функції більше за задану частину інтервалу. Вивчаємо цей процес на наступному прикладі.

Приклад$\PageIndex{3}$: Finding the Area of a Region Bounded by Functions That Cross

Якщо$\textbf{R}$ область між графіками функцій$\displaystyle f(x)=\sin x $ і$\displaystyle g(x)=\cos x$ над інтервалом$\displaystyle [0,π]$, знайдіть площу області$\textbf{R}$.

Рішення

Регіон зображений на наступному малюнку.

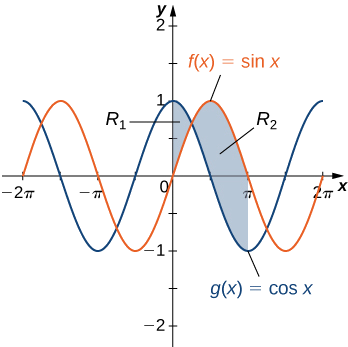
Ця цифра має два графіки. Ними є функції f (x) = sinx і g (x) = cosx. Вони обидва є періодичними функціями, які нагадують хвилі. Між графіками є дві затінені області. Перша затінена область позначена «R1» і має g (x) над f (x). Ця область починається з осі y і зупиняється там, де криві перетинаються. Друга область маркується «R2» і починається на перетині з f (x) вище g (x). Затінена область зупиняється на x=pi. — Малюнок$\PageIndex{5}$: Область між двома кривими може бути розбита на дві субобласті.

Графіки функцій перетинаються в$\displaystyle x=π/4$. Для$\displaystyle x∈[0,π/4], \cos x≥\sin x ,$ так

$\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\cos x−\sin x .$

З іншого боку, для$\displaystyle x∈[π/4,π], \sin x ≥\cos x,$ так

$\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\sin x −\cos x.$

Тоді

\[ \begin{align*} A =\int ^b_a|f(x)−g(x)|dx \\[4pt] =\int ^π_0|\sin x −\cos x|dx=\int ^{π/4}_0(\cos x−\sin x )dx+\int ^{π}_{π/4}(\sin x −\cos x)dx \\[4pt] =[\sin x +\cos x]|^{π/4}_0+[−\cos x−\sin x ]|^π_{π/4} \\[4pt] =(\sqrt{2}−1)+(1+\sqrt{2})=2\sqrt{2}. \end{align*}\]

Площа області -$\displaystyle 2\sqrt{2}$ одиниці ^₂.

Вправа$\PageIndex{3}$

Якщо$\textbf{R}$ область між графіками функцій$\displaystyle f(x)=\sin x $ і$\displaystyle g(x)=\cos x$ над інтервалом$\displaystyle [π/2,2π]$, знайдіть площу області$\textbf{R}$.

Підказка: Дві криві перетинаються на$\displaystyle x=(5π)/4.$

Відповідь: $\displaystyle 2+2\sqrt{2}$одиниць ²

Приклад$\PageIndex{4}$: Finding the Area of a Complex Region

Розглянемо область, зображену на малюнку$\PageIndex{6}$. Знайдіть площу$\textbf{R}$.

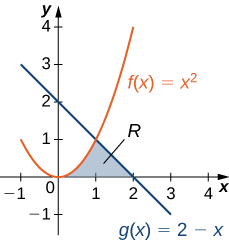
Ця цифра має два графіки в першому квадранті. Вони є функціями f (x) = x^2 і g (x) = 2-х. Між цими графіками знаходиться затінена область, обмежена зліва f (x), а праворуч g (x). Все це вище осі х. Область позначена R. Затінена область знаходиться між x=0 та x=2. — Малюнок$\PageIndex{6}$: Для обчислення площі цієї області потрібні два інтеграла.

Рішення

Як і в прикладі$\PageIndex{3}$, нам потрібно розділити інтервал на дві частини. Графіки функцій перетинаються в$\displaystyle x=1$ (set$\displaystyle f(x)=g(x)$ і вирішують для x), тому ми оцінюємо два окремих інтеграла: один через інтервал$\displaystyle [0,1]$ і один через інтервал$\displaystyle [1,2]$.

Протягом інтервалу$\displaystyle [0,1]$ область обмежена вище$\displaystyle f(x)=x^2$ і нижче по осі х, тому ми маємо

$\displaystyle A_1=\int ^1_0x^2dx=\dfrac{x^3}{3}∣^1_0=\dfrac{1}{3}.$

Протягом інтервалу$\displaystyle [1,2],$ область обмежена вище$\displaystyle g(x)=2−x$ і нижче по осі х, тому ми маємо

$\displaystyle A_2=\int ^2_1(2−x)dx=[2x−\dfrac{x^2}{2}]∣^2_1=\dfrac{1}{2}.$

Склавши ці області воєдино, отримуємо

$\displaystyle A=A_1+A_2=\dfrac{1}{3}+\dfrac{1}{2}=\dfrac{5}{6}.$

Площа області -$\displaystyle 5/6$ одиниці ²^.

Вправа$\PageIndex{4}$

Розглянемо регіон, зображений на наступному малюнку. Знайдіть площу$\textbf{R}$.

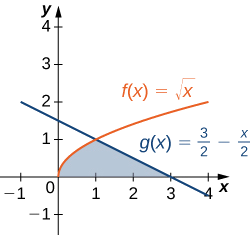
$Ця цифра має два графіки в першому квадранті. Вони є функціями f (x) = квадратний корінь x і g (x) = 3/2 — x/2. Між цими графіками знаходиться затінена область, обмежена зліва f (x), а праворуч g (x). Все це вище осі х. Затінена область знаходиться між x=0 та x=3.$

Підказка: Дві криві перетинаються на x = 1

Відповідь: $\displaystyle \dfrac{5}{3}$одиниць ²

Регіони, визначені стосовно y

У$\PageIndex{4}$ прикладі нам довелося оцінити два окремих інтеграла, щоб обчислити площу області. Однак є й інший підхід, який вимагає тільки одного інтеграла. Що робити, якщо ми розглядаємо криві як функції$\displaystyle y$, а не як функції$\displaystyle x$? Рецензія Малюнок. Зверніть увагу, що лівий графік, показаний червоним кольором, представлений функцією$\displaystyle y=f(x)=x^2$. Ми могли б так само легко вирішити це для х і представляти криву за допомогою функції$\displaystyle x=v(y)=\sqrt{y}$. ($\displaystyle x=−\sqrt{y}$Зауважте, що також є дійсним представленням функції$\displaystyle y=f(x)=x^2$ як функції$\displaystyle y$. Однак, виходячи з графіка, зрозуміло, що нас цікавить позитивний квадратний корінь.) Аналогічно, правий графік представлений функцією$\displaystyle y=g(x)=2−x$, але може так само легко бути представлений функцією$\displaystyle x=u(y)=2−y$. Коли графіки представлені у вигляді функцій$\displaystyle y$, ми бачимо, що область обмежена зліва графіком однієї функції, а праворуч - графіком іншої функції. Тому, якщо ми інтегруємо стосовно$\displaystyle y$, нам потрібно оцінити лише один інтеграл. Давайте розробимо формулу такого типу інтеграції.

$\displaystyle v(y)$Дозволяти$\displaystyle u(y)$ і бути безперервними функціями протягом інтервалу$\displaystyle [c,d]$ такий, що$\displaystyle u(y)≥v(y)$ для всіх$\displaystyle y∈[c,d]$. Ми хочемо знайти площу між графіками функцій, як показано на малюнку$\PageIndex{7}$.

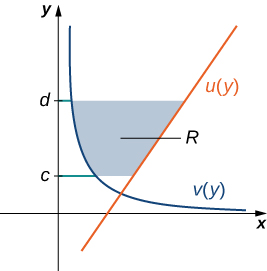
Ця цифра має два графіки в першому квадранті. Ними є функції v (y) і u (y). Між цими графіками знаходиться затінена область, обмежена зліва v (y), а праворуч u (y). Область позначена R. Затінена область знаходиться між горизонтальними межами y=c та y=d. — Малюнок$\PageIndex{7}$: Ми можемо знайти площу між графіками двох функцій,$\displaystyle u(y)$ і$\displaystyle v(y)$.

Цього разу ми збираємося розділити інтервал на осі y і використовувати горизонтальні прямокутники для наближення площі між функціями. Отже, для$\displaystyle i=0,1,2,…,n$, нехай$\displaystyle Q={y_i}$ буде звичайна перегородка$\displaystyle [c,d]$. Потім, для$\displaystyle i=1,2,…,n$, вибрати точку$\displaystyle y^∗_i∈[y_{i−1},y_i]$, потім на кожному інтервалі$\displaystyle [y_{i−1},y_i]$ побудувати прямокутник, який простягається горизонтально від$\displaystyle v(y^0∗_i)$ до$\displaystyle u(y^∗_i)$. $\PageIndex{8a}$На малюнку показані прямокутники, коли$\displaystyle y^∗_i$ вибрано нижню кінцеву точку інтервалу і$\displaystyle n=10$. $\PageIndex{8b}$На малюнку детально зображений представницький прямокутник.

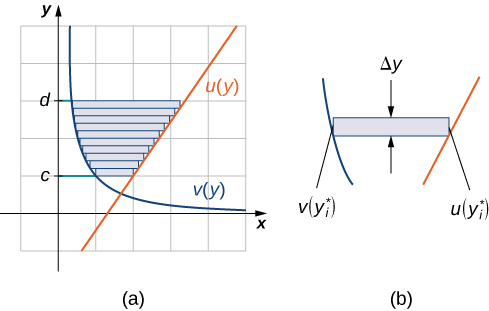
Ця цифра має три графіки. Перша цифра має дві криві. Ними є функції v (y*) і u (y*). Між цими кривими знаходиться горизонтальний прямокутник. Друга фігура, позначена «(a)», є затіненою областю, обмеженою ліворуч v (y), а праворуч - u (y). Затінена область знаходиться між горизонтальними межами y=c та y=d. Ця затінена область розбита на прямокутники між кривими. Третя цифра, позначена «(b)», є двома кривими v (y*) і u (y*). Між кривими знаходиться горизонтальний прямокутник з шириною дельта y. — Рисунок$\PageIndex{8}$: (а) Апроксимація площі між графами двох функцій,$\displaystyle u(y)$ і$\displaystyle v(y)$, з прямокутниками. (b) Площа типового прямокутника.

Висота кожного окремого прямокутника дорівнює$\displaystyle Δy$ і ширина кожного прямокутника дорівнює$\displaystyle u(y^∗_i)−v(y^∗_i)$. Тому площа між кривими приблизно

\[ A≈\sum_{i=1}^n[u(y^∗_i)−v(y^∗_i)]Δy . \nonumber \]

Це сума Рімана, тому ми приймаємо ліміт як$\displaystyle n→∞,$ отримання

\[ \begin{align*} A =\lim_{n→∞}\sum_{i=1}^n[u(y^∗_i)−v(y^∗_i)]Δy \\[4pt] =\int ^d_c[u(y)−v(y)]dy. \end{align*}\]

Ці висновки узагальнені в наступній теоремі.

Пошук площі між двома кривими, інтеграція вздовж осі y

Нехай$\displaystyle u(y)$ і$\displaystyle v(y)$ будуть безперервні функції такі, що$\displaystyle u(y)≥v(y) $ для всіх$\displaystyle y∈[c,d]$. Нехай$\textbf{R}$ позначають область, обмежену праворуч графіком$\displaystyle u(y)$, зліва - графіком$\displaystyle v(y)$, а вище і нижче лініями$\displaystyle y=d$ і$\displaystyle y=c$, відповідно. Потім площа$\textbf{R}$ задається

\[A=\int ^d_c[u(y)−v(y)]dy. \nonumber \]

Приклад$\PageIndex{5}$: Integrating with Respect to y

Давайте повернемося до Приклад$\PageIndex{4}$, тільки цього разу давайте інтегруватися по відношенню до$\displaystyle y$. $\textbf{R}$Дозволяти область, зображена на малюнку$\PageIndex{9}$. Знайти область$\textbf{R}$ шляхом інтеграції по відношенню до$\displaystyle y$.

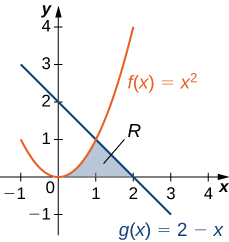
Рішення

Ми повинні спочатку висловити графіки як функції$\displaystyle y$. Як ми бачили на початку цього розділу, крива зліва може бути представлена функцією$\displaystyle x=v(y)=\sqrt{y}$, а крива праворуч може бути представлена функцією$\displaystyle x=u(y)=2−y$.

Тепер нам належить визначити межі інтеграції. Область обмежена нижче віссю x, тому нижня межа інтеграції є$\displaystyle y=0$. Верхня межа інтеграції визначається точкою, де перетинаються два графіки, яка є точкою$\displaystyle (1,1)$, тому верхня межа інтеграції є$\displaystyle y=1$. Таким чином, ми маємо$\displaystyle [c,d]=[0,1]$.

Розрахувавши площу регіону, отримуємо

\[ \begin{align*} A =\int ^d_c[u(y)−v(y)]dy \\[4pt] =\int ^1_0[(2−y)−\sqrt{y}]dy\\[4pt] =[2y−\dfrac{y^2}{2}−\dfrac{2}{3}y^{3/2}]∣^1_0\\[4pt] =\dfrac{5}{6}. \end{align*}\]

Площа області -$\displaystyle 5/6$ одиниці ².

Вправа$\PageIndex{5}$

Давайте повернемося до контрольної точки$\PageIndex{4}$, пов'язаної з Example, тільки цього разу давайте інтегруватися щодо$\displaystyle y$. $\textbf{R}$Дозволяти область, зображена на наступному малюнку. Знайти область$\textbf{R}$ шляхом інтеграції по відношенню до$\displaystyle y$.

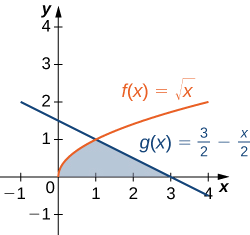
Підказка: Дотримуйтесь процесу з попереднього прикладу.

Відповідь: $\displaystyle \dfrac{5}{3}$одиниць ²

Ключові поняття

Подібно до того, як певні інтеграли можуть бути використані для пошуку площі під кривою, вони також можуть бути використані для пошуку площі між двома кривими.
Щоб знайти площу між двома кривими, визначеними функціями, інтегруйте різницю функцій.
Якщо графіки функцій перетинаються, або якщо область складна, використовують абсолютне значення різниці функцій. У цьому випадку може знадобитися оцінити два або більше інтегралів і додати результати, щоб знайти площу області.
Іноді це може бути простіше інтегрувати стосовно y, щоб знайти область. Принципи однакові незалежно від того, яка змінна використовується як змінна інтеграції.

Ключові рівняння

Площа між двома кривими, що інтегруються на осі x

$\displaystyle A=\int ^b_a[f(x)−g(x)]dx$

Площа між двома кривими, що інтегруються на осі y

$\displaystyle A=\int ^d_c[u(y)−v(y)]dy$

Пошук області між двома кривими

Приклад\(\PageIndex{1}\): Finding the Area of a Region between Two Curves I

Вправа\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\): Finding the Area of a Region between Two Curves II

Вправа\(\PageIndex{2}\)

Пошук площі області між кривими, що перетинаються

Приклад\(\PageIndex{3}\): Finding the Area of a Region Bounded by Functions That Cross

Вправа\(\PageIndex{3}\)

Приклад\(\PageIndex{4}\): Finding the Area of a Complex Region

Вправа\(\PageIndex{4}\)

Пошук площі між двома кривими, інтеграція вздовж осі y

Приклад\(\PageIndex{5}\): Integrating with Respect to y

Вправа\(\PageIndex{5}\)