Skip to main content
LibreTexts - Ukrayinska

1.24: Обсяг загальних твердих речовин

  1. Last updated
  2. Save as PDF
  • Page ID
    65855

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ванда Ортіс із «Залізних дівчат» збільшує обсяг.

    Ви можете використовувати калькулятор у цьому модулі.

    Примітка: Ми не обов'язково будемо дотримуватися правил округлення (точності та точності) в цьому модулі. Багато з цих цифр мають розміри лише з однією значною цифрою, але ми втратили б багато інформації, якби округлили результати лише до одного sig рис.

    У клавіші відповіді ми часто округляємо до найближчого цілого числа, або до найближчої десятої, або до двох-трьох значущих цифр, як ми вважаємо за потрібне.

    Площа поверхні твердого тіла - це сума площ всіх його граней; отже, площа поверхні двовимірна і вимірюється в квадратних одиницях. Обсяг - це кількість простору всередині твердого тіла. Обсяг тривимірний, вимірюється в кубічних одиницях. Ви можете уявити обсяг як кількість кубиків, необхідних для повного заповнення твердого тіла.

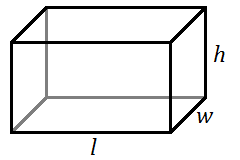
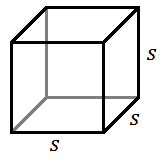
    тривимірна прямокутна коробка з нижнім переднім краєм з позначкою l, нижній правий край позначений w, і вертикальний правий край позначений hтривимірна квадратна коробка з нижнім переднім краєм позначені s, нижній правий край позначений s, і вертикальний правий край позначений s

    Об'єм прямокутного твердого тіла

    Для прямокутного твердого тіла з довжиною\(l\)\(w\), шириною та висотою\(h\):

    \[V=lwh \nonumber \]

    Для куба з довжиною сторони\(s\):

    \[V=s^3 \nonumber \]

    Вправи\(\PageIndex{1}\)

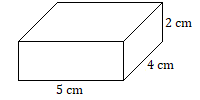
    Знайдіть обсяг кожного твердого тіла.

    1.

    2.

    Відповідь

    1. \(40\text{ cm}^3\)

    2. \(531\text{ cm}^3\)

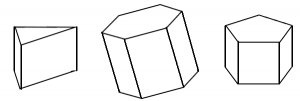
    Тверде тіло з двома рівнорозмірними багатокутниками в якості основ і прямокутними бічними гранями називається прямокутною призмою. Деякі приклади наведені нижче. Ми будемо називати їх просто призмами в цьому підручнику. (Ми не будемо працювати з косими призмами, які мають паралелограми для бічних граней.)

    Якщо ви знаєте площу однієї з підстав, множення її на висоту дає вам обсяг призми. У наведеній нижче формулі ми використовуємо капітал\(B\) для представлення площі підстави.

    Обсяг призми

    Для призми з базовою площею\(B\) і висотою\(h\):

    \[V=Bh \nonumber \]

    Якщо призма лежить на боці, то «висота» буде виглядати як довжина. Незалежно від того, як орієнтована призма, висота - це розмір, який перпендикулярний площинам двох паралельних основ.

    Вправи\(\PageIndex{1}\)

    Знайдіть обсяг кожної призми.

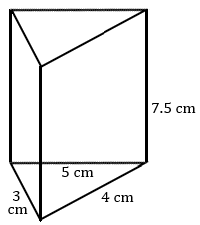
    3.

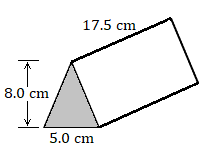
    4.

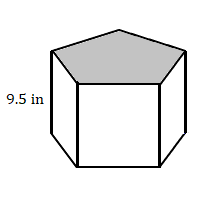
    5.

    Відповідь

    3. \(45\text{ cm}^3\)

    4. \(350\text{ cm}^3\)

    5. \(520\text{ cm}^3\)

    Площа п'ятикутника становить 55 квадратних дюймів.

    Циліндр можна розглядати як призму з основами, які є колами, а не багатокутниками. Так само, як і з призмою, обсяг - це площа підстави, помножена на висоту.

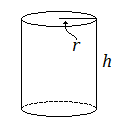
    Обсяг циліндра

    Для циліндра з радіусом\(r\) і висотою\(h\):

    \[V=\pi{r^2}h \nonumber \]

    Вправи\(\PageIndex{1}\)

    Знайдіть обсяг кожного циліндра.

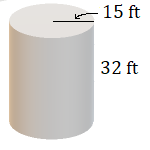
    6.

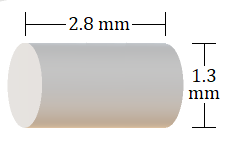
    7.

    Відповідь

    6. \(22,600\text{ ft}^3\)

    7. \(3.7\text{ mm}^3\)

    Як і у випадку з площею поверхні, нам потрібно буде використовувати обчислення, щоб отримати формулу об'єму сфери. Просто повірте. знизивши плечима смайли, вказуючи на те, що нам просто потрібно прийняти речі і рухатися далі

    Обсяг сфери

    Для сфери з радіусом\(r\):

    \[V=\dfrac{4}{3}\pi{r^3} \nonumber \]

    або

    \[V=4\pi{r^3}\div3 \nonumber \]

    Вправи\(\PageIndex{1}\)

    Знайдіть обсяг кожної сфери.

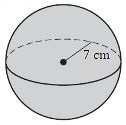
    8. куля радіусом 7 см

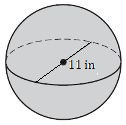
    9. сфера

    Відповідь

    8. \(1,440\text{ cm}^3\)

    9. \(7\overline{0}0\text{ in}^3\)

    Композитні тверді тіла

    Звичайно, не кожен тривимірний об'єкт - це призма, циліндр або сфера. Композитне тверде тіло складається з двох або більше простих твердих тіл. Як і у випадку з двовимірними складовими фігурами, розбиття фігури на впізнавані тверді тіла є хорошим першим кроком.

    Вправа\(\PageIndex{1}\)

    10. Заклепка утворюється шляхом доливання циліндра півсфери. Ширина циліндричної частини (шпильки заклепки) -\(1.6\) см, а довжина -\(7\) см. Ширина полусферической верхівки (головки заклепки) -\(3.2\) см. Знайдіть обсяг заклепки.

    Відповідь

    \(31.2\text{ cm}^3\)(об'єм циліндра\(\approx14.07\text{ cm}^3\) та об'єм півкулі\(\approx17.16\text{ cm}^3\).)