5.4: Рівновага зв'язку

При розгляді поліморфізму в одному генетичному локусі ми припускали два різних алелі,\(A\) і\(a\). Диплоїдний потім зустрічається як один з трьох типів:\(A A, A a\) і аа. Зараз ми розглянемо поліморфізм у двох генетичних локусах, кожен з яких має два різних алелі. Якщо алелі у перших генетичних локусів є\(A\) і\(a\), а ті у другого\(B\) і\(b\), то можливі чотири чіткі гаплоїдні гамети, а саме\(A B, A b, a B\) і\(a b\). Можливі десять різних диплотипів, отриманих шляхом формування пар всіх можливих гаплотипів. Ми можемо записати ці десять диплотипів як\(A B / A B, A B / A b, A B / a B, A B / a b\)\(A b / A b, A b / a B, A b / a b, a B / a B, a B / a b\)\(a b / a b\), і, де чисельник представляє гаплотип від одного з батьків, знаменник представляє гаплотип від іншого батька. Ми не розрізняємо тут, який гаплотип прийшов від якого батька.

Щоб продовжити далі, ми визначаємо алельні та гаметські частоти для нашої проблеми двох локусів у таблиці 5.13. Якщо ймовірність того, що гамета містить алель\(A\) або\(a\) не залежить від того, чи містить гамет аллель\(B\) або\(b\), то два локуси, як кажуть, незалежні. За припущенням незалежності гаметські частоти є добутками алельних частот\(p_{A B}=p_{A} p_{B}, p_{A b}=p_{A} p_{b}\), т. Е.

Найчастіше два локуси не є самостійними. Це може бути пов'язано з епістатичним виділенням, або епістазом. Як приклад, припустимо, що два локуси у людини впливають на висоту, і що найбільш підходящим генотипом є той, що призводить до середньої висоти. Вибір, який сприяє середній чисельності населення ознаки, називається нормалізуючим або стабілізуючим. Припустимо, що\(A\) і\(B\) є гіпотетичними високими алелями,\(a\) і\(b\) є короткими алелями, а людина з двома високими і двома короткими алелями отримує середню висоту. Тоді відбір може сприяти конкретним генотипам\(A B / a b, A b / A b, A b / a B\), і\(a B / a B\). Селекція може діяти як проти генотипів, що дають вище середньої висоти\(A B / A B, A B / A b\), так і тих, що дають нижче середньої висоти,\(A b / a b, a B / a b\) і\(a b / a b\).\(A B / a B\) Епістатичний виділення відбувається тому, що придатність\(A, a\) локусів залежить від того, які алелі присутні в\(B, b\) локусах. Тут\(A\) має вищу придатність, коли в парі з\(b\), ніж у парі з\(B\).

Два локуси також не можуть бути незалежними через кінцевий розмір популяції (тобто стохастичні ефекти). Наприклад, припустимо, що мутація\(a \rightarrow A\) відбувається лише один раз у кінцевій популяції (у нескінченній популяції будь-яка можлива мутація відбувається нескінченну кількість разів), і\(A\) це сильно сприяє природний відбір. Частота\(A\) може потім збільшитися. Якщо поруч знаходиться поліморфний локус на тій же хромосомі, що і\(A\) буває\(B\) (скажімо, при поліморфізмі\(b\) в популяції), то\(A B\) гамети можуть істотно збільшуватися в частоті, при цьому\(A b\) відсутні. Ми говоримо, що алель\(B\) подорожує автостопом з прихильним алелем\(A\).

Коли два локуси не є незалежними, ми говоримо, що локуси знаходяться в гаметічній фазі порушення рівноваги, або частіше порушення рівноваги зв'язку, іноді скорочено LD. Коли локуси незалежні, ми говоримо, що вони знаходяться в рівновазі зв'язку. Тут ми змоделюємо, як два локуси, спочатку в порушення рівноваги зв'язків, наближаються до рівноваги зв'язку через процес рекомбінації.

Для початку нам знадобиться рудиментарне розуміння мейозу. Під час мейозу

Таблиця 5.13: Визначення алельних та гаметських частот для двох генетичних локусів, кожен з двома алелями.

алель або гамет генотип	\(A\)	\(a\)	\(B\)	\(b\)	\(A B\)	\(A b\)	\(a B\)	\(a b\)
частоти	\(p_{A}\)	\(p_{a}\)	\(p_{B}\)	\(p_{b}\)	\(p_{A B}\)	\(p_{A b}\)	\(p_{a B}\)	\(p_{a b}\)

Малюнок 5.2: Схема перетину та рекомбінації під час мейозу (малюнок з Access Excellence @ Національний музей охорони здоров'я)

ДНК диплоїдної клітини, розташованої в дуже довгих молекулах, званих хромосомами, тиражується один раз і розділяється двічі, виробляючи чотири гаплоїдні клітини, кожна з яких містить половину хромосом вихідної клітини. Статеве розмноження призводить до сингамії, злиття гаплоїдної яйцеклітини та сперматозоїдів з утворенням диплоїдної клітини зиготи.

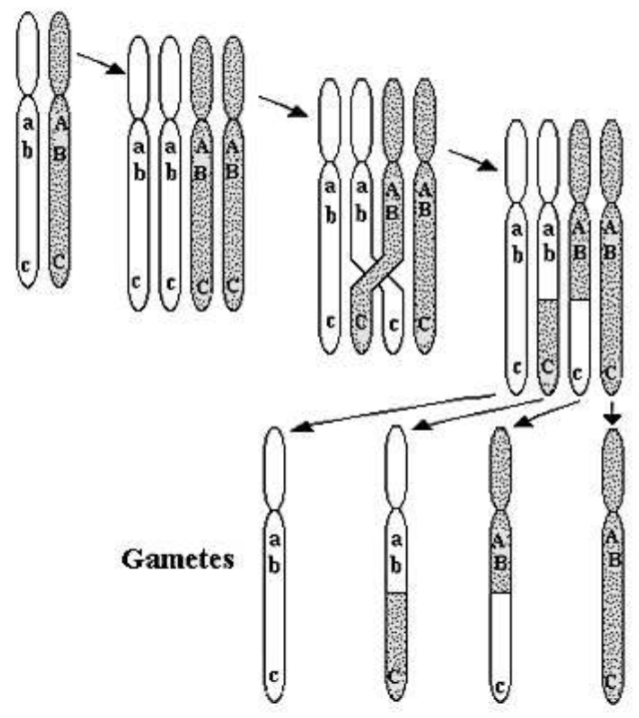
Рис. \(5.2\)представляє схему мейозу та процесу кросинг-оверу, що призводить до рекомбінації. У диплоїда кожна хромосома має відповідну сестринську хромосому, одну хромосому, що походить від яйцеклітини, одна зі сперматозоїда. Ці хромосоми братів і сестер мають однакові гени, але, можливо, різні алелі. На рис. 5.2 схематично покажемо алелі\(a, b, c\) на світлій хромосомі, а алелі -\(A, B, C\) на темній хромосомі сестри. На першому етапі мейозу кожна хромосома відтворює себе точно. На другому етапі сестринські хромосоми обмінюються генетичним матеріалом процесом схрещування. Потім всі чотири хромосоми розділяються на гаплоїдні клітини. Зверніть увагу на схему, що процес схрещування може призвести до генетичної рекомбінації. Припустимо, що схема рис. \(5.2\)являє собою вироблення сперми чоловіком. Якщо хромосома від батька самця містить алелі\(A B C\) і алелі від матері самця\(a b c\), рекомбінація може призвести до того, що сперма містить хромосому з алелями\(A B c\) (третя гамета на рис. 5.2). Ми говоримо, що ця хромосома є рекомбінантною; вона містить алелі як від діда по батькові, так і бабусі по батьківській лінії. Цілком ймовірно, що точного поєднання алелів на цій рекомбінантній хромосомі ніколи раніше не існувало у однієї людини. Рекомбінація - причина, чому всі, за винятком однакових близнюків, генетично унікальні.

Кажуть, що гени, що виникають на одній хромосомі, пов'язані між собою. Чим ближче гени знаходяться один до одного на хромосомі, тим щільніше зв'язок, і тим менше ймовірність їх розділить рекомбінація. Тісно пов'язані гени, швидше за все, будуть успадковані від того ж бабусі і дідуся. Гени на різних хромосомах за визначенням незв'язані; незалежний асортимент хромосом призводить до\(50 \%\) шансу отримати гамет або гени бабусь і дідусів. Для визначення та моделювання еволюції дисрівноваги зв'язків спочатку отримано алельні частоти з гаметічних частот шляхом

\[\begin{array}{ll} p_{A}=p_{A B}+p_{A b}, & p_{a}=p_{a B}+p_{a b} \\[4pt] p_{B}=p_{A B}+p_{a B}, & p_{b}=p_{A b}+p_{a b} \end{array} \nonumber \]

Оскільки частоти сумуються до одиниці,

\[p_{A}+p_{a}=1, \quad p_{B}+p_{b}=1, \quad p_{A B}+p_{A b}+p_{a B}+p_{a b}=1 . \nonumber \]

Існує три незалежні гаметські частоти і лише дві незалежні алельні частоти, тому загалом неможливо отримати гаметські частоти від алельних частот, не припускаючи додаткового обмеження, такого як рівновага зв'язку. Однак ми можемо ввести додаткову змінну\(D\), яка називається коефіцієнтом порушення рівноваги зв'язку, і\(D\) визначити різницю між гаметською частотою\(p_{A B}\) та якою буде ця гаметська частота, якби локуси були у зв'язку рівновага:

\[p_{A B}=p_{A} p_{B}+D \nonumber \]

Використовуючи\(p_{A B}+p_{A b}=p_{A}\) для усунення\(p_{A B}\) в (5.4.3), отримуємо

\[p_{A b}=p_{A} p_{b}-D \nonumber \]

Аналогічним чином, використовуючи\(p_{A B}+p_{a B}=p_{B}\)

\[p_{a B}=p_{a} p_{B}-D \nonumber \]

і використання\(p_{a b}+p_{a b}=p_{a}\)

\[p_{a b}=p_{a} p_{b}+D . \nonumber \]

З нашим визначенням, позитивний зв'язок порушення рівноваги\((D>0)\) передбачає надмірне\(A B\) і\(a b\) гамети і дефіцитні\(A b\) і\(a B\) гамети; негативний зв'язок порушення рівноваги\((D<0)\) передбачає протилежне. \(D\)досягає свого максимального значення\(1 / 4\) коли\(p_{A B}=\)\(p_{a b}=1 / 2\), і досягає мінімального значення\(-1 / 4\) коли\(p_{A b}=p_{a B}=1 / 2\). Рівність, отримана з (5.4.3, 5.4.4, 5.4.5, 5.4.6), яку ми пізніше вважаємо корисною, є

\[\begin{align} \nonumber p_{A B} p_{a b}-p_{A b} p_{a B} &=\left(p_{A} p_{B}+D\right)\left(p_{a} p_{b}+D\right)-\left(p_{A} p_{b}-D\right)\left(p_{a} p_{B}-D\right) \\[4pt] \nonumber &=D\left(p_{A} p_{B}+p_{a} p_{b}+p_{A} p_{b}+p_{a} p_{B}\right) \\[4pt] &=D \end{align} \nonumber \]

Без виділення і мутації\(D\) еволюціонує тільки через рекомбінації. З простими числами, що представляють значення в наступному поколінні, і використовуючи\(p_{A}^{\prime}=p_{A}\) і\(p_{B}^{\prime}=p_{B}\) тому, що статеве розмноження само по собі не змінює частот алелів,

\[\begin{aligned} D^{\prime} &=p_{A B}^{\prime}-p_{A}^{\prime} p_{B}^{\prime} \\[4pt] &=p_{A B}^{\prime}-p_{A} p_{B} \\[4pt] &=p_{A B}^{\prime}-\left(p_{A B}-D\right) \\[4pt] &=D+\left(p_{A B}^{\prime}-p_{A B}\right), \end{aligned} \nonumber \]

де ми використали (5.4.3) для отримання третьої рівності. Таким чином\(D\), зміна дорівнює зміні частоти\(A B\) гамет,

\[D^{\prime}-D=p_{A B}^{\prime}-p_{A B} \nonumber \]

Таблиця 5.14: Обчислення частот гамет.

		gamete безкоштовно/диплоїдний безкоштовно
диплоїдний	занурення фрек	AB	Аб	aB	аб
\(A B / A B\)	\(p_{A B}^{2}\)	1	0	0	0
\(A B / A b\)	\(2 p_{A B} p_{A b}\)	\(1 / 2\)	\(1 / 2\)	0	0
\(A B / a B\)	\(2 p_{A B} p_{a B}\)	\(1 / 2\)	0	\(1 / 2\)	0
\(A B / a b\)	\(2 p_{A B} p_{a b}\)	\((1-r) / 2\)	\(r / 2\)	\(r / 2\)	\((1-r) / 2\)
\(A b / A b\)	\(p_{A b}^{2}\)	0	1	0	0
\(A b / a B\)	\(2 p_{A b} p_{a B}\)	\(r / 2\)	\((1-r) / 2\)	\((1-r) / 2\)	\(r / 2\)
\(A b / a b\)	\(2 p_{A b} p_{a b}\)	0	\(1 / 2\)	0	\(1 / 2\)
\(a B / a B\)	\(p_{a B}^{2}\)	0	0	1	0
\(a B / a b\)	\(2 p_{a B} p_{a b}\)	0	0	\(1 / 2\)	\(1 / 2\)
\(a b / a b\)	\(p_{a b}^{2}\)	0	0	0	1

Щоб зрозуміти, чому гаметичні частоти змінюються між поколіннями, ми повинні спочатку визнати, коли вони не змінюються. Без генетичної рекомбінації хромосоми підтримують свою точну ідентичність між поколіннями. Частоти хромосом без рекомбінації тому постійні, а для генетичних локусів на одній хромосомі з алелями\(\mathrm{A}, \mathrm{a}\) і\(\mathrm{B}, \mathrm{b}\), скажімо,\(p_{A B}^{\prime}=p_{A B} .\) в нескінченній популяції без виділення або мутації гаметні частоти змінюються тільки для генетичних локусів при порушенні рівноваги зв'язків на різних хромосомах, або для генетичних локусів при порушенні рівноваги зв'язків на одній хромосомі, що піддається генетичній рекомбінації.

Обчислимо\(p_{A B}^{\prime}\) частоту\(A B\) гамет в наступному поколінні, враховуючи\(p_{A B}\) частоту\(A B\) гамет в нинішньому поколінні, використовуючи два різних методи. Перший спосіб використовує стіл в'язки. Другий метод робить прямий аргумент ймовірності.

Таблиця в'язки наведена в таблиці 5.14. Перша колонка - батьківський диплотип до мейозу. Другий стовпець - це частота диплотипу, яка передбачає випадкове спаровування. Наступні чотири колонки - частоти гаплоїдного генотипу (нормовані відповідними диплоїдними частотами для спрощення представлення таблиці). Тут ми\(r\) визначаємо частоту, з якою гамета виникає внаслідок поєднання генів бабусі та дідуся. Якщо\(B, b\) локуси\(A, a\) і виникають на одній хромосомі, то\(r\) це частота рекомбінації за рахунок кросинг-оверу. Якщо\(\mathrm{B}, \mathrm{b}\) локуси\(\mathrm{A}, \mathrm{a}\) і зустрічаються на різних хромосомах, то через самостійного асортименту хромосом існує однакова ймовірність того, що гамета містить всі дідусеві або бабусині гени, або містить комбінацію генів бабусі і діда, так що\(r=1 / 2\). Зверніть увагу, що кросінговер або незалежний асортимент має важливе значення для тих пар генів, для яких внесок діда і бабусі в диплоїдний генотип не мають спільних алелів (тобто\(A B / a b\) і\(A b / a B\) генотипів). Частота\(p_{A B}^{\prime}\) в наступному поколінні задається сумою\(A B\) стовпця (після множення на диплоїдні частоти). Тому

\[\begin{align} \nonumber p_{A B}^{\prime} &=p_{A B}^{2}+p_{A B} p_{A b}+p_{A B} p_{a B}+(1-r) p_{A B} p_{a b}+r p_{A b} p_{a B} \\[4pt] \nonumber &=p_{A B}\left(p_{A B}+p_{A b}+p_{a B}+p_{a b}\right)+r\left(p_{A b} p_{a B}-p_{A B} p_{a b}\right) \\[4pt] &=p_{A B}-r D \end{align} \nonumber \]

де кінцева рівність використовує\((5.4.2)\) і (5.4.7).

Другий спосіб обчислень\(p_{A B}^{\prime}\) більш прямий. \(A B\)Гаплотип може виникнути у диплоїда загального типу\(A B / X X\) без рекомбінації, або диплоїда типу\(A X / X B\) з рекомбінацією. Тому

\[p_{A B}^{\prime}=(1-r) p_{A B}+r p_{A} p_{B} \nonumber \]

де перший член - від нерекомбінантних, а другий - від рекомбінантів. З\(p_{A} p_{B}=p_{A B}-D\), у нас є

\[\begin{aligned} p_{A B}^{\prime} &=(1-r) p_{A B}+r\left(p_{A B}-D\right) \\[4pt] &=p_{A B}-r D \end{aligned} \nonumber \]

той же результат, що і\((5.4.9)\).

Використовуючи\((5.4.8)\) і\((5.4.9)\), виводимо

\[D^{\prime}=(1-r) D, \nonumber \]

з розчином

\[D_{n}=D_{0}(1-r)^{n} \nonumber \]

Рекомбінація зменшує порушення рівноваги зв'язку в кожному поколінні в рази\((1-r)\). Тісно пов'язані гени на одній хромосомі мають невеликі значення\(r\); незв'язані гени на різних хромосомах мають\(r=1 / 2\). Для незв'язаних генів порушення рівноваги зв'язків зменшується в два рази в кожному поколінні. Зроблено висновок, що для підтримки дисбалансу зв'язків генів на різних хромосомах необхідний дуже сильний відбір, тоді як слабкий відбір може підтримувати порушення рівноваги зв'язків для щільно пов'язаних генів.