8.7: Вправи

Last updated
Save as PDF

Page ID: 66281

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Навички

Марко в даний час має 20 тюльпанів у своєму дворі. Щороку він садить ще 5.
1. Напишіть рекурсивну формулу для кількості тюльпанів, які має Марко
2. Напишіть явну формулу для кількості тюльпанів Марко має

Пем - диск-жокей. Щотижня вона купує 3 нові альбоми, щоб зберегти свою колекцію актуальною. В даний час вона володіє 450 альбомів.
1. Напишіть рекурсивну формулу для кількості альбомів, які має Pam
2. Напишіть явну формулу для кількості альбомів, які має Pam

Продажі магазину (в тисячах доларів) зростають відповідно до рекурсивного правила$P_n=P_{n-1} + 15$, з початковою чисельністю населення$P_0=40$.
1. Розрахувати$P_1$ і$P_2$
2. Знайдіть явну формулу для$P_n$
3. Використовуйте свою формулу, щоб передбачити продажі магазину через 10 років
4. Коли продажі магазину перевищать 100 000 доларів?

Кількість будинків у місті зростає відповідно до рекурсивного правила$P_n=P_{n-1} + 30$, з початковим населенням$P_0=200$.
1. Розрахувати$P_1$ і$P_2$
2. Знайдіть явну формулу для$P_n$
3. Використовуйте свою формулу, щоб передбачити кількість будинків за 10 років
4. Коли кількість будинків досягне 400 будинків?

Популяція жуків зростає за лінійною моделлю росту. Початкова популяція (тиждень 0) була$P_0=3$, а населення після 8 тижнів -$P_8=67$.
1. Знайдіть явну формулу популяції жуків за тиждень$n$
2. Через скільки тижнів популяція жука досягне 187?

Кількість вуличних ліхтарів у місті зростає лінійно. Чотири місяці тому$(n = 0)$ було 130 вогнів. Зараз$(n = 4)$ є 146 ліхтарів. Якщо ця тенденція збережеться,
1. Знайдіть явну формулу для кількості світильників у місяці$n$
2. Скільки місяців знадобиться, щоб досягти 200 вогнів?

Населення Такоми в 2000 році становило близько 200 тисяч, і щорічно зростало приблизно на 9%.
1. Напишіть рекурсивну формулу для населення Такома
2. Напишіть явну формулу для населення Такома
3. Якщо ця тенденція збережеться, яким буде населення Такоми в 2016 році?
4. Коли ця модель прогнозує чисельність населення Такоми перевищить 400 тисяч?

Населення Портленда в 2007 році становило близько 568 тисяч, і щорічно зростало приблизно на 1,1%.
1. Напишіть рекурсивну формулу для населення Портленд
2. Напишіть явну формулу для населення Портленд
3. Якщо ця тенденція збережеться, яким буде населення Портленда в 2016 році?
4. Якщо ця тенденція збережеться, коли населення Портленда досягне 700 тисяч?

Хвороби мають тенденцію поширюватися відповідно до експоненціальної моделі зростання. У перші дні СНІДу темпи зростання становили близько 190%. У 1983 році близько 1700 чоловік в США померли від СНІДу. Якби ця тенденція продовжувалася безконтрольно, скільки людей померло б від СНІДу в 2005 році?

Населення світу в 1987 році становило 5 мільярдів, а річний темп приросту оцінювався в 2 відсотки на рік. Припускаючи, що населення світу дотримується моделі експоненціального зростання, знайдіть прогнозоване населення світу в 2015 році.

Запускають культуру бактерій з 300 бактерій. Через 4 години популяція виросла до 500 бактерій. Якщо населення зростає в геометричній прогресії,
1. Напишіть рекурсивну формулу для кількості бактерій
2. Напишіть явну формулу для кількості бактерій
3. Якщо ця тенденція збережеться, скільки бактерій буде за 1 день?
4. Скільки часу потрібно, щоб культура потроїлася в розмірах?

Рідний вид вовків був знову введений в національний ліс. Спочатку було пересаджено 200 вовків. Через 3 роки популяція зросла до 270 вовків. Якщо населення зростає в геометричній прогресії,
1. Напишіть рекурсивну формулу для кількості вовків
2. Напишіть явну формулу для кількості вовків
3. Якщо ця тенденція збережеться, скільки вовків буде через 10 років?
4. Якщо ця тенденція збережеться, скільки часу знадобиться популяції, щоб вирости до 1000 вовків?

Сто форелі висівають в озеро. Відсутність обмежень, їх населення буде рости на 70% в рік. Озеро може витримати максимум 2000 форелі. Використовуючи модель логістичного зростання,
1. Напишіть рекурсивну формулу для кількості форелі
2. Розрахуйте кількість форелі через 1 рік і через 2 роки.

У моєму дворі почали рости десять рослин ожини. Відсутність обмежень, ожина буде поширюватися на 200% на місяць. Мій двір може витримати лише близько 50 рослин. Використовуючи модель логістичного зростання,
1. Напишіть рекурсивну формулу для кількості рослин ожини на моєму дворі
2. Розрахуйте кількість рослин через 1, 2 і 3 місяці

У 1968 році мінімальна заробітна плата США становила 1,60 долара на годину. У 1976 році мінімальна заробітна плата становила $2,30 на годину. Припустимо, що мінімальна заробітна плата зростає відповідно до експоненціальної моделі, де n представляє час у роках після 1960 року.
1. Знайдіть явну формулу мінімальної заробітної плати.
2. Що прогнозує модель для мінімальної заробітної плати в 1960 році?
3. Якщо мінімальна заробітна плата становила $5,15 в 1996 році, це вище, нижче або дорівнює тому, що прогнозує модель?

Поняття

Населення невеликого містечка можна описати рівнянням$P_n = 4000 + 70n$, де$n$ знаходиться кількість років після 2005 року. Поясніть словами, що це рівняння говорить нам про те, як змінюється населення.

Населення невеликого містечка можна описати рівнянням$P_n = 4000(1.04)n$, де$n$ знаходиться кількість років після 2005 року. Поясніть словами, що це рівняння говорить нам про те, як змінюється населення.

Розвідка

Більшість прикладів у тексті розглядаються зростаючі величини, але лінійні та експоненціальні рівняння також можуть описувати зменшуються величини, оскільки будуть досліджуватися наступні кілька проблем.

Нова вантажівка коштує 32 000 доларів. Вартість автомобіля з часом знеціниться, а значить втратить вартість. Для цілей оподаткування амортизація зазвичай розраховується лінійно. Якщо вантажівка коштує 24 500 доларів через три роки, напишіть явну формулу вартості автомобіля через$n$ роки.

Інфляція змушує речі коштувати дорожче, а за наші гроші купувати менше (звідси ваші бабусі і дідусі кажуть: «У мій день ви могли б купити чашку кави за нікель»). Припустимо, інфляція щороку знижує вартість грошей на 5%. Іншими словами, якщо у вас є $1 цього року, наступного року він придбає вам лише 0,95 доларів. Скільки $100 ви купите за 20 років?

Припустимо, що у вас є миска з 500 цукерок M&M, і кожен день ви їсте$\frac{1}{4}$ цукерок, які у вас є. Чи змінюється кількість цукерок, що залишилися лінійно або експоненціально? Напишіть рівняння для моделювання кількості цукерок, що залишилися через n днів.

Теплий предмет в більш прохолодному приміщенні буде знижуватися в геометричній прогресії, наближаючись до кімнатної температури за формулою, де Tn$r$ - температура через n хвилин, - швидкість, з якою змінюється температура, а - постійна, а Tr - температура приміщення. Судово-медичні слідчі можуть використовувати це для прогнозування часу смерті жертви вбивства. Припустимо, що коли тіло було виявлено$(n = 0)$, це було 85 градусів. Через 20 хвилин знову виміряли температуру до 80 градусів. Тіло знаходилося в кімнаті 70 градусів.
1. Використовуйте наведену інформацію з наданою формулою, щоб знайти формулу температури тіла.
2. Коли померла потерпіла, якщо тіло почалося в 98,6 градуса?

Рекурсивні рівняння можуть бути дуже зручними для моделювання складних ситуацій, для яких явні рівняння важко інтерпретувати. Як приклад розглянемо озеро, в якому в даний час проживає 2000 риб. Популяція риби щорічно зростає на 10%, але щороку 100 риб збирають з озера людьми, що займаються риболовлею.
1. Напишіть рекурсивне рівняння для кількості риб у озері через n років.
2. Обчисліть чисельність населення після 1 і 2 років. Здається, що населення збільшується або зменшується?
3. Яка максимальна кількість риби, яку можна збирати щороку, не викликаючи зменшення популяції риби в довгостроковій перспективі?

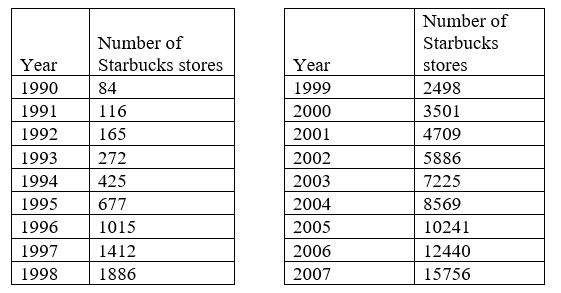
Кількість магазинів Starbucks зросла після першого відкриття. Кількість магазинів за 1990-2007 роки, як повідомляється на їх корпоративному сайті [1], наведено нижче.
1. Ретельно збудуйте дані. Чи здається, змінюється лінійно або експоненціально?
2. Спробуйте знайти рівняння для моделювання даних, вибравши дві точки для роботи. Наскільки добре рівняння моделює дані?
3. Спробуйте використовувати рівняння виду, де k - константа, для моделювання даних. Цей тип моделі називається моделлю Power. Порівняйте свої результати з результатами з частини$b$. Примітка: щоб використовувати цю модель, вам потрібно буде мати 1990 відповідає,$n = 1$ а не$n = 0$.

$clipboard_e723972894bc819360fb5aa9fe3e212fd.png$

Томас Мальтус був економістом, який висунув принцип, що населення зростає на основі експоненціальної моделі зростання, тоді як продовольство та ресурси ростуть на основі лінійної моделі зростання. Виходячи з цього, Мальтус передбачив, що в кінцевому підсумку попит на їжу та ресурси переросте пропозицію, з наслідками приреченості та похмурості. Проведіть деякі дослідження про Мальтуса, щоб відповісти на ці питання.
1. Які соціальні зміни запропонував Мальтус, щоб уникнути приреченості та похмурості, який він прогнозував?
2. Як ви думаєте, чому його прогнози не відбулися?
3. Які подібності та відмінності між теорією Мальтуса та моделлю логістичного зростання?

[1] www.starbucks.com/Про нас/Компанія_Timeline.pdf отримано травень 2009