9.4: Фундаментальна теорема алгебри

Алгебра над комплексними числами багато в чому простіше, ніж над дійсними числами. Причина в тому, що многочлен ступеня\(N\) in\(\mathbb{C}[z]\) має точно\(N\) нулі, рахуючи кратність. Це називається фундаментальною теоремою алгебри. Щоб це довести, ми повинні встановити деякі попередні результати.

Деякий аналіз.

ВИЗНАЧЕННЯ. Ми говоримо, що послідовність\(\left\langle z_{n}=x_{n}+i y_{n}\right\rangle\) комплексних чисел сходиться до числа\(z=x+i y\) iff\(\left\langle x_{n}\right\rangle\) сходиться до\(x\) і\(\left\langle y_{n}\right\rangle\) сходиться до\(y\). Ми говоримо, що послідовність Коші, якщо обидва\(\left\langle x_{n}\right\rangle\) і\(\left\langle y_{n}\right\rangle\) є Коші.

ЗАУВАЖЕННЯ. Це те саме, що говорити, що\(\left\langle z_{n}\right\rangle\) сходиться до\(z\) iff\(\left|z-z_{n}\right|\) прагне до нуля, і\(\left\langle z_{n}\right\rangle\) це Коші iff\[(\forall \varepsilon>0)(\exists N)(\forall m, n>N)\left|z_{m}-z_{n}\right|<\varepsilon .\] ВИЗНАЧЕННЯ. Нехай\(G \subseteq \mathbb{C}\). Ми говоримо, що функція\(f: G \rightarrow \mathbb{C}\) є безперервним на\(G\) якщо, всякий раз, коли\(\left\langle z_{n}\right\rangle\) є послідовність в\(G\), що сходиться до\(z_{\infty}\) деякого значення в\(G\), потім\(\left\langle f\left(z_{n}\right)\right\rangle\) сходиться \(f\left(z_{\infty}\right)\).

ПРОПОЗИЦІЯ 9.34. Поліноми є неперервними функціями на\(\mathbb{C}\).

Доказ. Повторіть доказ Пропозиції\(5.23\) з комплексними числами замість дійсних чисел.

ВИЗНАЧЕННЯ. Замкнутий прямокутник - це набір форми\(\{z \in \mathbb{C} \mid a \leq\)\(\Re(z) \leq b, c \leq \Im(z) \leq d\}\) для деяких дійсних чисел\(a \leq b\) і\(c \leq d\). Ми хотіли б отримати версію теореми про екстремальні значення, але незрозуміло, як слід визначати мінімальне та максимальне значення комплексної функції. Однак наше визначення безперервності має сенс, навіть якщо діапазон\(f\) міститься в\(\mathbb{R}\), і кожна складноцінна безперервна функція\(g\) має три природно пов'язані реальні неперервні функції, а саме.\(\Re(g), \Im(g)\) і \(|g|\).

ТЕОРЕМА 9.35. \(R\)Дозволяти бути замкнутий прямокутник в\(\mathbb{C}\), і\(f: R \rightarrow \mathbb{R} a\) безперервна функція. Потім\(f\) досягає свого максимуму і мінімуму.

Доказ. Нехай\(R=\{z \in \mathbb{C} \mid a \leq \Re(z) \leq b, c \leq \Im(z) \leq d\}\). \(\left\langle z_{n}=x_{n}+i y_{n}\right\rangle\)Дозволяти послідовність точок такі, що\(f\left(z_{n}\right)\) прагне або до найменшої верхньої межі діапазону\(f\), якщо це існує, або нехай\(f\left(z_{n}\right)>n\) для всіх\(n\), якщо діапазон не обмежений вище. За теоремою БольцаноВайєрштрасса 8.6 існує певна підпослідовність, для якої дійсні частини сходяться до деякого числа\(x_{\infty}\) в\([a, b]\). За Больцано-Вейерштрассом знову, деяка підпослідовність цієї підпослідовності має властивість, що уявні частини також сходяться, в якийсь момент\(y_{\infty}\) в\([c, d]\). Отже, замінивши вихідну послідовність цією підпослідовністю, можна вважати, що\(z_{n}\) сходиться до точки\(z_{\infty}=x_{\infty}+i y_{\infty} \in R\). За безперервності,\(f\left(z_{\infty}\right)=\lim _{n \rightarrow \infty} f\left(z_{n}\right)\). Якщо початкова послідовність була необмеженою, то\(f\left(z_{n}\right)>n\) в підпослідовності. Це неможливо, оскільки послідовність\(\left\langle f\left(z_{n}\right)\right\rangle\) сходиться до\(f\left(z_{\infty}\right)\). Тому підпослідовність обмежена і\(f\left(z_{\infty}\right)\) повинна бути найменшою верхньою межею діапазону\(f\). \(f\left(z_{\infty}\right)\)Тому максимум\(f\) більше\(R\).

Подібний аргумент показує, що досягається і мінімум.

ЗАУВАЖЕННЯ. Попередню теорему можна вдосконалити, щоб показати, що безперервна дійсна функція на замкнутій обмеженій множині\(\mathbb{C}\) досягає своєї крайності. Множина\(F\) закривається, якщо всякий раз, коли послідовність точок\(\left\langle z_{n}\right\rangle\) сходиться до деякого комплексного числа\(z_{\infty}\), то\(z_{\infty}\) знаходиться в\(F\). Набір обмежується, якщо він міститься в якомусь прямокутнику.

Потрібен ще один геометричний факт. ЛЕМА 9.36. Нерівність трикутника\(z_{1}, z_{2}\) Дозволяти комплексні числа. Тоді\[\left|z_{1}+z_{2}\right| \leq\left|z_{1}\right|+\left|z_{2}\right|\]

ФІГУРА\(9.18\). Нерівність трикутника

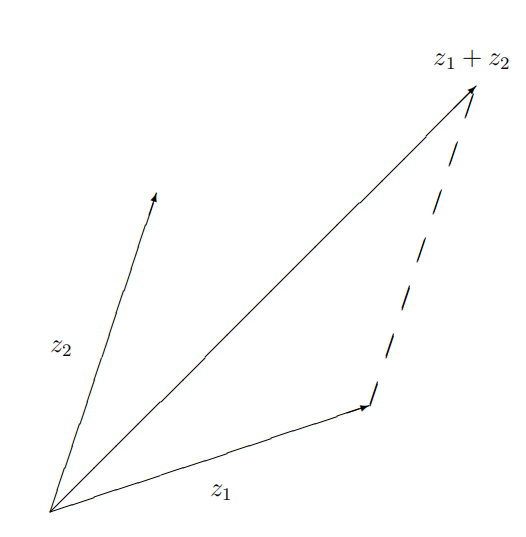
Доказ. Напишіть\(z_{1}=r_{1} \operatorname{Cis}\left(\theta_{1}\right)\) і\(z_{2}=r_{2} \operatorname{Cis}\left(\theta_{2}\right)\). Потім\[\begin{aligned} \left|r_{1} \operatorname{Cis}\left(\theta_{1}\right)+r_{2} \operatorname{Cis}\left(\theta_{2}\right)\right| \\ &=\left[\left(r_{1} \cos \theta_{1}+r_{2} \cos \theta_{2}\right)^{2}+\left(r_{1} \sin \theta_{1}+r_{2} \operatorname{si}\right.\right.\\ &=\left[r_{1}^{2}+r_{2}^{2}+2 r_{1} r_{2}\left(\cos \theta_{1} \cos \theta_{2}+\sin \theta_{1} \sin \theta_{2}\right)\right] \\ &=\left[r_{1}^{2}+r_{2}^{2}+2 r_{1} r_{2} \cos \left(\theta_{1}-\theta_{2}\right)\right]^{1 / 2} \\ & \leq\left[r_{1}^{2}+r_{2}^{2}+2 r_{1} r_{2}\right]^{1 / 2} \\ &=r_{1}+r_{2} . \end{aligned}\] слідство 9.38. Нехай\(z_{1}, \ldots, z_{n} \in \mathbb{C}\). Тоді\[\left|z_{1}+\cdots+z_{n}\right| \leq\left|z_{1}\right|+\cdots+\left|z_{n}\right| .\]

Доказ фундаментальної теореми алгебри.

Спочатку ми спостерігаємо, що пошук коренів і пошук факторів тісно пов'язані між собою.

ЛЕМА 9.39. \(p\)Дозволяти поліном ступеня\(N \geq 1\) в\(\mathbb{C}[z]\). Комплексне\(c\) число - це корінь\(p\) iff,\[p(z)=(z-c) q(z),\] де\(q\) многочлен ступеня\(N-1\).

Доказ. Повторіть доказ Лемми\(4.13\) з дійсними числами, заміненими комплексними числами.

Тепер доведено лему Д'Аламберта, яка стверджує, що модуль полінома не може мати локального мінімуму, окрім як у корені.

ЛЕМА 9.40. Лемма\(p \in \mathbb{C}[z]\) Д'Аламбера Нехай і\(\alpha \in \mathbb{C}\). Якщо\(p(\alpha) \neq 0\), то\[(\forall \varepsilon>0)(\exists \zeta)[|\zeta-\alpha|<\varepsilon] \wedge[|p(\zeta)|<|p(\alpha)|]\] Доказ. Фікс\(\alpha\), а не корінь\(p\). Запишіть\(p\) як\[p(z)=\sum_{k=0}^{N} a_{k}(z-\alpha)^{k},\] де\(a_{0}\) ні\(a_{N}\) ні 0. Нехай\[m=\min \left\{j \in \mathbb{N}^{+} \mid a_{j} \neq 0\right\} .\] так\[p(z)=a_{0}+a_{m}(z-\alpha)^{m}+\cdots+a_{N}(z-\alpha)^{N} .\] нехай\(a_{0}=r_{0} \operatorname{Cis}\left(\theta_{0}\right)\) і\(a_{m}=r_{m} \operatorname{Cis}\left(\theta_{m}\right)\). Ми\(\zeta\) виберемо форму таким\[\zeta=\alpha+\rho \operatorname{Cis}(\phi)\] чином, щоб отримати деяке скасування в перші два терміни (9.42). Отже, нехай\[\phi=\frac{\theta_{0}+\pi-\theta_{m}}{m} .\] Тоді\[a_{0}+a_{m}(\zeta-\alpha)^{m}=r_{0} \operatorname{Cis}\left(\theta_{0}\right)-r_{m} \rho^{m} \operatorname{Cis}\left(\theta_{0}\right) .\] залишається показати, що для досить\(\rho\) малих ми можемо ігнорувати всі умови вищого порядку. Зверніть увагу, що якщо\(\rho<1\), у нас є\[\begin{aligned} \left|a_{m+1}(\zeta-\alpha)^{m+1}+\cdots+a_{N}(\zeta-\alpha)^{N}\right| \\ & \leq\left|a_{m+1}(\zeta-\alpha)^{m+1}\right|+\cdots+\left|a_{N}(\zeta-\alpha)^{N}\right| \\ &=\left|a_{m+1}\right| \rho^{m+1}+\cdots+\left|a_{N}\right| \rho^{N} \\ & \leq \rho^{m+1}\left[\left|a_{m+1}\right|+\cdots+\left|a_{N}\right|\right] \\ &=: C \rho^{m+1} . \end{aligned}\] Вибрати\(\rho\) так, що\(r_{m} \rho^{m}<r_{0}\). Тоді\[p(\zeta)=\left(r_{0}-r_{m} \rho^{m}\right) \operatorname{Cis}\left(\theta_{0}\right)+a_{m+1}(\zeta-\alpha)^{m+1}+\cdots+a_{N}(\zeta-\alpha)^{N},\]\(\mathrm{SO}\)\[|p(\zeta)| \leq r_{0}-r_{m} \rho^{m}+C \rho^{m+1} .\] якщо\(\rho<r_{m} / C\), права сторона (9.43) менше, ніж\(r_{0}\).

Отже, ми робимо висновок, що приймаючи\[\rho=\frac{1}{2} \min \left(1, \frac{r_{m}}{C},\left[\frac{r_{0}}{r_{m}}\right]^{1 / m}, \varepsilon\right)\] потім\[\zeta=\rho \operatorname{Cis}\left(\frac{\theta_{0}+\pi-\theta_{m}}{m}\right)\] задовольняє висновок леми.

ТЕОРЕМА 9.44. Фундаментальна теорема алгебри\(p \in \mathbb{C}[z]\) Дозволяти бути поліном ступеня\(N \geq 1\). Тоді\(p\) можуть бути враховані як\[p(z)=c\left(z-\alpha_{1}\right) \ldots\left(z-\alpha_{N}\right)\] для комплексних чисел\(c, \alpha_{1}, \ldots, \alpha_{N}\). Крім того, факторинг є унікальним під замовлення. Доказ. (i) Показати, що\(p\) має принаймні один корінь.

Нехай\(p(z)=\sum_{k=0}^{N} a_{k} z^{k}\), з\(a_{N} \neq 0\). \(S\)Дозволяти бути замкнутим квадратом\(\{z \in \mathbb{C} \mid-L \leq \Re(z) \leq L,-L \leq \Im(z) \leq L\}\), де\(L\) є деяке (велике) число, яке буде вибрано пізніше.

Якщо\(|z|=R\) потім\[\left|\sum_{k=0}^{N-1} a_{k} z^{k}\right| \leq \sum_{k=0}^{N-1}\left|a_{k}\right| R^{k} .\] вибрати\(L_{0}\) так, що якщо\(R \geq L_{0}\),\[\sum_{k=0}^{N-1}\left|a_{k}\right| R^{k} \leq \frac{1}{2}\left|a_{N}\right| R^{N} .\] то якщо, то якщо\(L \geq L_{0}\) і\(z\) знаходиться зовні\(S\), у нас є\[\begin{aligned} \left|a_{N} z^{N}\right| &=\left|p(z)-\sum_{k=0}^{N-1} a_{k} z^{k}\right| \\ & \leq|p(z)|+\left|\sum_{k=0}^{N-1} a_{k} z^{k}\right| \\ & \leq|p(z)|+\frac{1}{2}\left|a_{N}\right| L^{N}, \end{aligned}\] де перший нерівність - це нерівність трикутника, а друге тому що\(|z|>L\). Вибираємо\(L_{1}\) такі, що\[\frac{1}{2}\left|a_{N}\right| L_{1}^{N}>\left|a_{0}\right| .\] нехай\(L=\max \left(L_{0}, L_{1}\right)\), і нехай\(S\) буде відповідний закритий квадрат. Функція\(|p|\) є безперервною\(S\), тому вона досягає свого мінімуму в якийсь момент,\(\alpha_{1}\) скажімо, за теоремою 9.35. На кордоні\(S\), ми знаємо\[|p(z)| \geq \frac{1}{2}\left|a_{N}\right| L^{N}>\left|a_{0}\right|=|p(0)| .\] Тому\(\alpha_{1}\) повинні бути в інтер'єрі\(S\). За лемою D'Alembert, ми повинні мати\(p\left(\alpha_{1}\right)=0\), інакше буде поруч точка\(\zeta\), також в\(S\), де\(|p(\zeta)|\) було менше, ніж\(\left|p\left(\alpha_{1}\right)\right|\). Так\(\alpha_{1}\) і корінь\(p\).

(ii) Тепер ми застосовуємо Lemma,\(9.39\) щоб зробити висновок, що ми можемо фактор,\(p\) як\[p(z)=\left(z-\alpha_{1}\right) q(z)\] де\(q\) є поліном ступеня\(N-1\). За допомогою простого індукційного аргументу ми можемо\(p\) враховувати\(N\) лінійні фактори.

(iii) Унікальність очевидна. Число\(c\) - коефіцієнт\(a_{N}\). Числа\(a_{k}\) - це саме ті точки, в яких функція\(p\) зникає, як випливає з Пропозиції,\(9.19\) що добуток скінченно багатьох комплексних чисел може бути 0 тоді і тільки тоді, коли одне з чисел саме по собі 0.