9.2: Комплексні числа
- Page ID
- 65727
ВИЗНАЧЕННЯ. Комплексне число Комплексне число - це вираз виду\(a+i b\), де\(a\) і\(b\) є дійсними числами.
На даний момент ви можете думати про\(i\) in\(a+i b\) як про формальний символ, або місце власника. Пізніше ми побачимо, що воно має інше тлумачення.
Позначення. \(\mathbb{C}\)Давайте\(\mathbb{C}\) позначимо множини всіх комплексних чисел:\[\mathbb{C}=\{a+i b: a, b \in \mathbb{R}\} .\] Як множина, можна ідентифікувати\(\mathbb{C}\) з\(\mathbb{R}^{2}\) очевидним чином. Це дозволяє нам визначити додавання; що не так очевидно, це те, що існує також гарне визначення для множення.
ВИЗНАЧЕННЯ. \(c+i d\)Дозволяти\(a+i b\) і бути комплексними числами. Тоді їх сума і добуток визначаються\[\begin{aligned} (a+i b)+(c+i d) &=(a+c)+i(b+d) \\ (a+i b) \times(c+i d) &=(a c-b d)+i(a d+b c) . \end{aligned}\] формулою для суми (9,14) саме те, що ви отримаєте, якби ви ідентифікували комплексне число\(a+i b\) з вектором\((a, b)\) в\(\mathbb{R}^{2}\) і використовували векторне додавання. Продукт більш тонкий. Якщо помножити ліву частину (9.15), ви отримаєте\[a c+i(a d+b c)+i^{2} b d .\] Один приходить праворуч від (9.15), визначаючи\[i^{2}=-1 \text {. }\] Так\(i\) квадратний корінь\(-1\); тобто це алгебраїчна величина, яку ми вводимо, яка визначена для мають властивість, що його площа\(-1\). Очевидно, що це\(i\) виключає реальне число.
По суті, ми продовжили програму визначення систем числення, яку ми розпочали в главі 8. Додавання та множення комплексних чисел визначено алгебраїчними операціями на\(\mathbb{R} \times \mathbb{R}\). Оскільки алгебраїчні операції над дійсними числами були визначені множинно-теоретично, ми тим самим визначили алгебраїчні операції\(\mathbb{C}\) по множинним операціям. На відміну від інших систем чисел, які ми визначили, ми не визначаємо лінійне впорядкування\(\mathbb{C}\). Як правило, не корисно думати про комплексні числа на числовому рядку. Однак дуже корисно думати про комплексні числа як точки на площині\(\mathbb{R}^{2}\), і описувати їх у полярних координатах.
Як завжди, точка з декартовими координатами\((x, y)\) має полярні координати\((r, \theta)\), де вони пов'язані\[\begin{array}{cl} r=\sqrt{x^{2}+y^{2}} & \tan (\theta)=y / x \\ x=r \cos \theta & y=r \sin \theta . \end{array}\] Таким чином комплексне число також\(z=x+i y\) може бути записано як\[z=r(\cos \theta+i \sin \theta) .\] Форма (9.18) настільки широко використовується, що існує спеціальні позначення для нього.
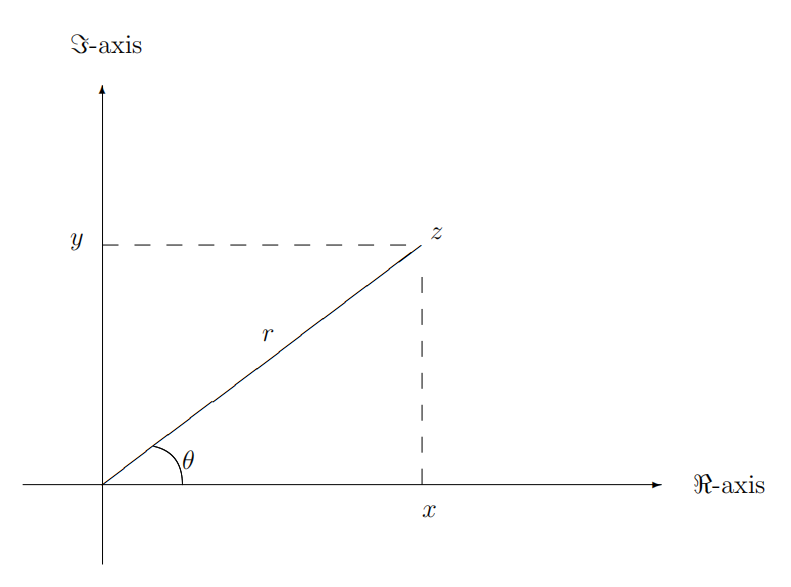
Позначення. Cis\[\operatorname{Cis}(\theta):=\cos \theta+i \sin \theta .\] ВИЗНАЧЕННЯ. Для комплексного числа\(z=x+i y=r \operatorname{Cis}(\theta)\) ми маємо наступне:
\(\Re(z) x\)називається реальна частина\(z\), написана\(\Re(z)\);
\(\Im(z) y\)називається уявна частина\(z\), написана\(\Im(z)\);
\(|z| r\)називається модулем або абсолютним значенням\(z\), записаним\(|z|\);\(\arg (z) \theta\) називається аргументом\(z\), записаним\(\arg (z)\).\(z\)
\(\bar{z}\)Число\(x-i y\) називається сполученим з\(z\), написаним\(\bar{z}\).
ЗАУВАЖЕННЯ. Існує важливий момент, який слід пам'ятати про аргумент: він є унікальним лише до додавання кратних\(2 \pi\). Іншими словами, якщо\(\theta_{0}\) аргумент комплексного числа\(z\), то так і всі числа\(\left\{\theta_{0}+2 k \pi: k \in \mathbb{Z}\right\}\). Додавання найпростіше в декартових координатах: додайте реальну та уявну частини. Множення найпростіше в полярних координатах: множте модулі та додайте аргументи.
Пропозиція 9.19. Нехай\(z_{1}=r_{1} \operatorname{Cis}\left(\theta_{1}\right)\) і\(z_{2}=r_{2} \operatorname{Cis}\left(\theta_{2}\right)\). Потім\[z_{1} z_{2}=r_{1} r_{2} \operatorname{Cis}\left(\theta_{1}+\theta_{2}\right) .\] ProOf. Помноживши, отримаємо результат\[\begin{aligned} z_{1} z_{2}=r_{1} r_{2}\left[\cos \theta_{1} \cos \theta_{2}-\sin \theta_{1} \sin \theta_{2}\right.\\ &\left.+i\left(\cos \theta_{1} \sin \theta_{2}+\cos \theta_{2} \sin \theta_{1}\right)\right] . \end{aligned}\] за тригонометричними тотожностями для косинуса і синуса суми двох кутів.
Наслідком Пропозиції\(9.19\) є наступна формула для підняття комплексного числа до степеня, яка називається теоремою Де Муавра.
ТЕОРЕМА 9.20. Теорема Де Муавра\(z=r \operatorname{Cis}(\theta)\) Дозволяти бути ненульовим комплексним числом, і нехай\(n \in \mathbb{Z}\). Потім\[z^{n}=r^{n} \operatorname{Cis}(n \theta) .\] ProOf. Якщо\(n \geq 0\), то\((9.21)\) можна довести індукцією з Пропозиції 9.19. Для\(n\) негативних достатньо спостерігати, що за допомогою пропозиції\(9.19\)\[[r \operatorname{Cis}(\theta)]\left[r^{-1} \operatorname{Cis}(-\theta)\right]=1 \operatorname{Cis}(0)=1 .\] Ми можемо довести, що кожне ненульове комплексне число має точно\(n\) чіткі\(n^{\text {th }}\) коріння.
ТЕОРЕМА 9.22. \(z=r \operatorname{Cis}(\theta)\)Дозволяти бути ненульовим комплексне число, і\(n\) нехай ціле число більше 1. Тоді є точно\(n\) комплексні числа, що\(w\) задовольняють рівнянню\(w^{n}=z\). Вони є\[\left\{r^{1 / n} \operatorname{Cis}\left(\frac{\theta}{n}+\frac{2 k \pi}{n}\right): k=0,1, \ldots, n-1\right\} .\] доказом. Припустимо,\(w=\rho \operatorname{Cis}(\phi)\) це\(n^{\text {th }}\) корінь\(z\). Тоді за теоремою Де Муавра,\(\rho^{n}=r\) і\(n \phi\) є аргументом\(z\). Як і\(\rho\) має бути позитивним дійсним числом, це унікальний позитивний\(n^{\text {th }}\) корінь\(r\). Число\(n \phi\) може бути будь-який аргумент\(z\), так що у нас є\[n \phi=\theta+2 k \pi, \quad k \in \mathbb{Z} .\] Так\(\phi\) може мати форму\[\frac{\theta}{n}+\frac{2 k \pi}{n}\] для будь-якого цілого числа\(k\). Однак різні\(\phi\) породжують одне і те ж комплексне число,\(w\) якщо вони відрізняються кратним\(2 \pi\). Так що є точно\(n\) різні\(w\) 's, які є\(n^{\text {th }}\) корінням\(z\).
ПРИКЛАД 9.24. Що Теорема\(9.22\) говорить нам квадратні коріння\(-1\)? Допускаємо\(r=1\) і\(\theta=\pi\), і отримуємо квадратні коріння\(\operatorname{Cis}(\pi / 2)=i\) і\(\operatorname{Cis}(-\pi / 2)=-i\).
ПРИКЛАД 9.25. Знайти куб коріння\(1 .\)
У позначеннях теореми\(9.22, r=1\) і\(\theta=0\). Тому кубічні\[\begin{aligned} 1 &=\operatorname{Cis}(2 \pi / 3)=-\frac{1}{2}+i \frac{\sqrt{3}}{2} \\ \omega^{2} &=\operatorname{Cis}(4 \pi / 3)=-\frac{1}{2}-i \frac{\sqrt{3}}{2} . \end{aligned}\] корені є Число\(\omega\) називається примітивним кубовим коренем одиниці, тому що всі кубові коріння виходять як\(\omega, \omega^{2}, \omega^{3}\).
ВИЗНАЧЕННЯ. Примітивний корінь єдності Примітивний\(n^{\text {th }}\) корінь єдності - це число\(\omega\) таке, що\(\left\{1, \omega, \omega^{2}, \ldots, \omega^{n-1}\right\}\) складають всі\(n^{\text {th }}\) коріння 1.
Пропозиція 9.26. \(z\)Дозволяти складне число, і\(w_{0}\) бути деяким\(n^{\text {th }}\) коренем\(z\). Нехай\(\omega\) буде примітивний\(n^{\text {th }}\) корінь єдності. Потім все\(n^{\text {th }}\) коріння\(z\) знаходяться\(\left\{w_{0}, \omega w_{0}, \omega^{2} w_{0}, \ldots, \omega^{n-1} w_{0}\right\}\).
