9.1: Кубіки

Як знайти коріння кубічного многочлена? Вавилоняни знали квадратичну формулу ще в другому тисячолітті до нашої ери, але формула кубічного була знайдена лише в\(16^{\text {th }}\) столітті. Історія відкриття складна, але велика частина кредиту повинна йти Ніколо Тарталья. Рішення було опубліковано в 1545 році в дуже впливовій книзі Джироломо Кардано Artis magnae sive de regulis algebraicis liber unus. Формула\(9.2\) відома сьогодні як формула Тарталья-Кардано. Для історичного рахунку див. Наприклад, [6].

Розглянемо кубічний многочлен в\(\mathbb{R}[x]\)\[p(x)=a_{3} x^{3}+a_{2} x^{2}+a_{1} x+a_{0} .\] Якщо ми хочемо знайти коріння, немає втрати спільності в\(p\) припущенні\(a_{3}=1\), що, оскільки нулі збігаються з нулями\(\frac{1}{a_{3}} p\).

Друге спрощення полягає в тому, що ми можемо припустити\(a_{2}=0\). Дійсно, зробити зміну\[x=y-\beta,\] змінної,\(\beta\) щоб деякі були обрані пізніше. Потім\[\begin{aligned} p(x) &=x^{3}+a_{2} x^{2}+a_{1} x+a_{0} \\ &=(y-\beta)^{3}+a_{2}(y-\beta)^{2}+a_{1}(y-\beta)+a_{0} \\ &=y^{3}+\left[a_{2}-3 \beta\right] y^{2}+\left[a_{1}-2 a_{2} \beta+3 \beta^{2}\right] y+\left[a_{0}-a_{1} \beta+a_{2} \beta^{2}-\beta^{3}\right] \\ &=: \quad q(y) . \end{aligned}\] виберіть\(\beta=a_{2} / 3\). Потім коефіцієнт\(y^{2}\) in\(q(y)\) зникає. Припустимо, що можна знайти коріння\(q\), назвіть їх\(\alpha_{1}, \alpha_{2}, \alpha_{3}\). Тоді коріння вихідного многочлена\(p\) знаходяться\(\alpha_{1}-\beta, \alpha_{2}-\beta, \alpha_{3}-\beta\).

Тому достатньо знайти формулу для коренів кубічного, в якому квадратичний член зникає. Це називається зменшеним кубічним. Оскільки зараз залишилося лише два коефіцієнти, ми скинемо індекси і запишемо наш зменшений кубічний як\[q(x)=x^{3}+a x+b .\] Ключова ідея полягає в тому, щоб зробити іншу, більш геніальну, підміну. Введемо нову змінну\(w\), пов'язану\(x\) з\[x=w+\frac{c}{w},\] де\(c\) є константою, яку ми виберемо пізніше. Потім\[\begin{aligned} q(x) &=\left(w+\frac{c}{w}\right)^{3}+a\left(w+\frac{c}{w}\right)+b \\ &=w^{3}+[3 c+a] w+\left[3 c^{2}+a c\right] \frac{1}{w}+c^{3} \frac{1}{w^{3}}+b . \end{aligned}\] Виберіть\[c=-\frac{a}{3},\], щоб обидва коефіцієнт\(w\) і\(1 / w\) в (9.4) зникли. Потім знайти\(x\) так, що\(q(x)=0\) це те саме, що знайти\(w\) так, що\[\begin{aligned} w^{3}+\frac{c^{3}}{w^{3}}+b &=0 \\ \Longleftrightarrow w^{6}+b w^{3}+c^{3} &=0 . \end{aligned}\] рівняння (9.5) має ступінь 6, що здається гіршим, ніж оригінальний кубічний; але так багато термінів зникають, що це насправді квадратне рівняння в \(w^{3}\). Тому вона може вирішуватися за квадратичною формулою:\[w^{3}=\frac{-b \pm \sqrt{b^{2}-4 c^{3}}}{2} .\] Знаючи\(w\), ми можемо відновитися\(x\)\[x=w+\frac{c}{w}=w-\frac{a}{3 w} .\] Таким чином, ми приходимо до формули Тарталії - Кардано для коренів зменшеної кубічної (9.2):\[x=\left[\frac{-b \pm \sqrt{b^{2}+\frac{4 a^{3}}{27}}}{2}\right]^{1 / 3}-\frac{a}{3\left[\frac{-b \pm \sqrt{b^{2}+\frac{4 a^{3}}{27}}}{2}\right]^{1 / 3}} .\] Як формула працює на практиці?

ПРИКЛАД 9.8. Нехай\(p(x)=x^{3}-3 x+2\). Потім\(c=1\), і (9.6) говорить\(w^{3}=-1\). \(w=-1\)Тому і так\(x=-2\) є корінь. Тому Лемма\(4.13,(x+2)\) є фактором\(p\). Факторинг, ми\[x^{3}-3 x+2=(x+2)\left(x^{2}-2 x+1\right) .\] отримуємо останній термін фактори як\((x-1)^{2}\), тому робимо висновок, що коріння є\(-2,1,1\).

У прикладі 9.8 формула спрацювала, але лише дала нам одне з коренів. Розглянемо наступний приклад:

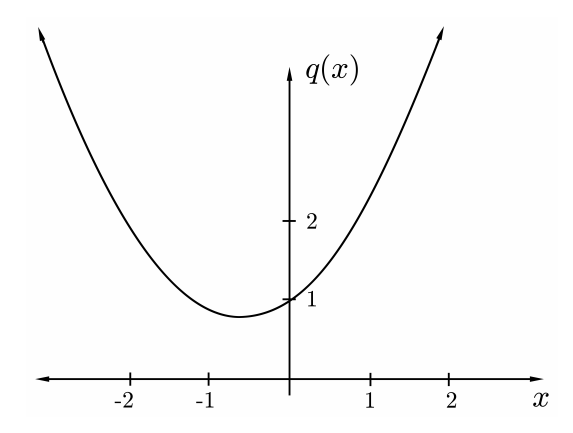
ПРИКЛАД 9.9. Нехай\[p(x)=x^{3}-3 x+1 .\] Тоді\(c=1\), і\[w^{3}=\frac{-1 \pm \sqrt{-3}}{2} .\] Тепер у нас є гірша проблема:\(w^{3}\) включає квадратний корінь негативного числа, і навіть якщо ми маємо сенс цього, ми потім повинні витягти куб корінь. Це аналогічно спробі вирішити квадратне рівняння\[q(x):=x^{2}+x+1=0 ?\] Квадратична формула знову дає праву частину\((9.11)\), і ми пояснюємо це тим, що насправді не\(q\) має реальних коренів. Дійсно, графіка показує, що\(q\) виглядає як рис. 9.12.

МАЛЮНОК 9.12. Сюжет\(q(x)=x^{2}+x+1\)

Але це не може бути так\(p\). Дійсно,\[\begin{aligned} p(-2) &=-1<0 \\ p(0) &=1>0 \\ p(1) &=-1<0 \\ p(2) &=3>0 \end{aligned}\] Отже, за теоремою проміжного значення\(8.10, p\) повинен мати корінь в кожному з інтервалів\((-2,0),(0,1)\) і\((1,2)\). Як\(p\) може мати не більше 3 коренів за теоремою\(4.10\), отже, він повинен мати рівно три корені. Графік\(p\) виглядає як рис. 9.13.

Виявляється, можна знайти коріння\(p\) в\(9.9\) Прикладі, правильно інтерпретувавши формулу Тартаглія-Кардано. Ми повернемося до цього прикладу в розділі 9.3, після того як розробимо необхідні ідеї. Велика ідея полягає в тому, щоб ввести поняття комплексного числа.