1.6: Послідовності
- Page ID
- 65726
У обчисленні ми думаємо про послідовність як (можливо, нескінченний) список об'єктів. Ми трохи розширимо цю ідею і висловимо її мовою функцій.
Кінцевою послідовністю є функція\(f\) з доменом\(\ulcorner N\urcorner\), де\(N \in \mathbb{N}\). Ми часто ототожнюємо послідовність з упорядкованим скінченним множиною\(\left\langle a_{n} \mid n<N\right\rangle\)\(a_{n}=f(n)\), де, для\(0 \leq n<N\).
Ця інтерпретація послідовності як типу функції легко поширюється на нескінченні послідовності.
Нескінченна послідовність - це функція\(f\) з доменом\(\mathbb{N}\). Ми часто ототожнюємо послідовність з упорядкованим нескінченним набором\(\left\langle a_{n} \mid n \in \mathbb{N}\right\rangle\)\(a_{n}=f(n)\), де, для\(n \in \mathbb{N}\).
ЗАУВАЖЕННЯ. Інтервал in\(\mathbb{Z}\) Насправді послідовність слів зазвичай використовується для означення будь-якої функції, область якої є інтервалом в\(\mathbb{Z}\), де інтервал в\(\mathbb{Z}\) є перетином деякого реального інтервалу с\(\mathbb{Z}\). Для зручності в цій книзі ми зазвичай вважаємо, що перший елемент будь-якої послідовності індексується 0 або 1.
\(\langle 0,1,4,9, \ldots\rangle\)Послідовність задається функцією\(f(n)=n^{2} .\)
Послідовність\(\langle 1,-1,2,-2,3,-3, \ldots\rangle\) задається функцією\[f(n)= \begin{cases}\frac{n}{2}+1, & n \text { even } \\ -\frac{n+1}{2}, & n \text { odd. }\end{cases}\] Sequences може приймати значення в будь-якому множині (кодомен функції\(f\), що визначає послідовність). Ми говоримо про реальну послідовність, якщо значення є дійсними числами, цілої послідовності, якщо вони всі цілі числа і т.д. пізніше з'ясується, що послідовності зі значеннями в наборі двох елементів\(\{0,1\}\) зустрічаються досить часто, тому у нас є спеціальна назва для них: ми називаємо їх двійковими послідовностями.
Кінцева двійкова послідовність є функцією\(f:\ulcorner N\urcorner \rightarrow\ulcorner 2\urcorner\), для деяких\(N \in \mathbb{N}\). Нескінченна двійкова послідовність - це функція,\(f: \mathbb{N} \rightarrow\ulcorner 2\urcorner\).
Ми часто використовуємо вираз\(\left\langle a_{n}\right\rangle\) для послідовності\(\left\langle a_{n} \mid n \in \mathbb{N}\right\rangle\).
Функції також використовуються для «індексування» множин з метою побудови більш складних множин з узагальненими операціями множини. Ми обговорили об'єднання (або перетин) більш ніж двох множин. Ви можете запитати, чи можна утворювати об'єднання або перетину великої (нескінченної) колекції множин. Є дві проблеми, які слід вирішити, відповідаючи на це питання. Ми повинні бути впевнені, що визначення об'єднання нескінченно багатьох множин є точним; тобто воно однозначно характеризує об'єкт у математичному всесвіті. Нам також потрібні позначення для управління цією ідеєю - як ми вказуємо множини, над якими ми приймаємо союз?
Для\(n \in \mathbb{N}^{+}\), нехай\(X_{n}\) буде набір. Тоді\[\bigcup_{n=1}^{\infty} X_{n}=\left\{x \mid \text { for some } n \in \mathbb{N}^{+}, x \in X_{n}\right\} \text {. }\]\(\mathbb{N}^{+}\) множиною називається набір індексу для об'єднання.
Це може бути написано кількома різними способами.
ПОЗНАЧЕННЯ. \(\bigcup_{n \in \mathbb{N}^{+}} X_{n}\)Наступні три вирази однакові:
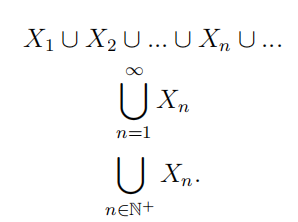
Ми можемо використовувати набори індексів, крім\(\mathbb{N}^{+}\).
Нехай\(A\) буде набір, а для\(\alpha \in A\), нехай\(X_{\alpha}\) буде набір. \[\mathcal{F}=\left\{X_{\alpha} \mid \alpha \in A\right\}\]Множиною називається сімейство множин, індексованих по\(A\). Потім\[\bigcup_{\alpha \in A} X_{\alpha}=\left\{x \mid x \in X_{\alpha} \text { for some } \alpha \in A\right\} \text {. }\]\(\bigcup_{\alpha \in A} X_{\alpha}\) читається позначення «об'єднання над альфою в A множин X sub alpha». Отже,\[x \in \bigcup_{\alpha \in A} X_{\alpha} \text { if } x \in X_{\alpha} \text { for some } \alpha \in A \text {. }\] загальні перетину над сімейством множин визначаються аналогічно:\[\bigcap_{\alpha \in A} X_{\alpha}=\left\{x \mid x \in X_{\alpha} \text { for all } \alpha \in A\right\} .\] приклад 1.43. Нехай\(X_{n}=\{n+1, n+2, \ldots, 2 n\}\) для кожного\(n \in \mathbb{N}^{+}\). Тоді\[\begin{aligned} &\bigcup_{n=1}^{\infty} X_{n}=\{k \in \mathbb{N} \mid k \geq 2\} \\ &\bigcap_{n=1}^{\infty} X_{n}=\emptyset . \end{aligned}\] приклад 1.44. Для кожного позитивного дійсного числа\(t\), нехай\(Y_{t}=[11 / t, t]\). Тоді\[\begin{aligned} \bigcup_{t \in(\sqrt{11}, \infty)} Y_{t} &=\mathbb{R}^{+} \\ \bigcap_{t \in[\sqrt{11}, \infty)} Y_{t} &=\{\sqrt{11}\} . \end{aligned}\] приклад 1.45. Нехай\(f: X \rightarrow Y, A \subseteq X\) і\(B \subseteq Y\). Потім\[\bigcup_{a \in A}\{f(a)\}=f[A] .\] і\[\bigcup_{b \in B} f^{-1}(b)=f^{-1}[B] .\]
