1.5: Зображення та інверси
- Page ID
- 65717
Функції можуть бути використані для визначення підмножин заданих множин.
Нехай\(f: X \rightarrow Y\) і\(W \subseteq X\). Зображення\(W\) під\(f\), написане\(f[W]\), є безліччю\[\{f(x) \mid x \in W\} .\] Так якщо\(f: X \rightarrow Y\), то\[\operatorname{Ran}(f)=f[X] .\] ПРИКЛАД 1.30. Припустимо,\(f\) це реальна функція\(f(x)=x^{2}+3\). Нехай\(W=\{-2,2,3\}\), і\(Z=(-1,2)\). Потім\(f[W]=\{7,12\}\), і\(f[Z]=[3,7)\).
У додатках математики функції часто описують числові зв'язки між вимірними спостереженнями. Так що якщо\(f: X \rightarrow Y\) і\(a \in X\), то\(f(a)\) це прогнозоване або фактичне вимірювання, пов'язане з\(a\). У цьому контексті часто цікавить визначення того, які елементи\(X\) пов'язані зі значенням\(b\), в кодомені\(f\).
Нехай\(f: X \rightarrow Y\) і\(b \in Y\). Тоді зворотне зображення\(b\) under\(f, f^{-1}(b)\), є множиною\[\{x \in X \mid f(x)=b\} .\] Цей набір також називається попереднім зображенням\(b\) під\(f\).
Зверніть увагу, що якщо\(b \notin \operatorname{Ran}(f)\), то\(f^{-1}(b)=\emptyset\). Якщо\(f\) це ін'єкція, то для будь-якої\(b \in \operatorname{Ran}(f), f^{-1}(b)\) є єдиний елемент.
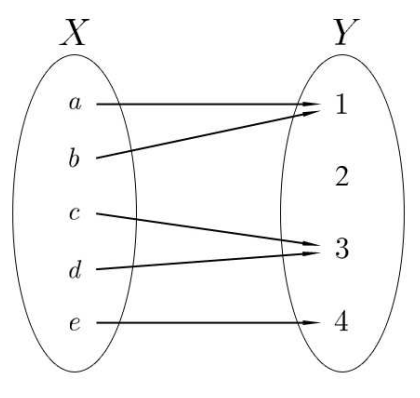
Нехай\(f: X \rightarrow Y\) і\(Z \subseteq Y\). Обернене зображення\(Z\) under\(f\), або попереднє зображення\(Z\) under\(f\), є множиною\[f^{-1}[Z]=\{x \in X \quad \mid f(x) \in Z\}\] Ми використовуємо\(f^{-1}[]\) для означення зворотного зображення підмножини кодомену, і\(f^{-1}\) () для зворотного зображення елемента кодомена - обидва є підмножинами області\(f\). Якщо\(Z \cap \operatorname{Ran}(f)=\emptyset\), то\[f^{-1}[Z]=\emptyset .\] приклад 1.32. \(f\)Дозволяти бути як на малюнку\(1.33\) тоді\(f[\{b, c\}]=\{1,3\}\), і\(f^{-1}[\{1,3\}]=\{a, b, c, d\}\).
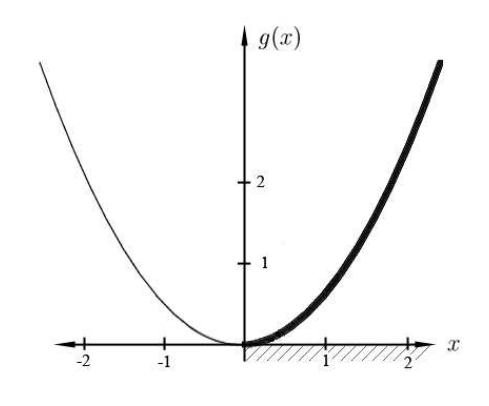
\(g\)Дозволяти бути реальною функцією\(g(x)=x^{2}+3\). Якщо\(b \in \mathbb{R}\) і\(b>3\), то\[g^{-1}(b)=\{\sqrt{b-3},-\sqrt{b-3}\} .\] якщо\(b=3\), то\(g^{-1}(3)=\{0\}\). Якщо\(b<3\), то\(g^{-1}(b)\) порожній.
\(h\)Дозволяти бути реальною функцією\(h(x)=e^{x}\). Якщо\(b \in \mathbb{R}\) і\(b>0\), то\[h^{-1}(b)=\left\{\log _{e}(b)\right\} .\] Наприклад,\[h^{-1}(1)=\{0\} .\]\(h\) тому що суворо збільшується, зворотне зображення будь-якого елемента codomain\((\mathbb{R})\) є або множиною з одним елементом або порожнім набором.
Нехай\(I=(a, b)\), де\(a, b \in \mathbb{R}\) і\(0<a<b\) (\(I\)тобто відкритий інтервал з кінцевими точками\(a\) і\(b\)). Потім\[h^{-1}[I]=\left(\log _{e}(a), \log _{e}(b)\right) .\] ми обговорили побудову нових функцій з існуючих функцій з використанням алгебраїчних операцій та складу функцій. Ще одним інструментом побудови нових функцій з відомих функцій є зворотна функція.
Нехай\(f: X \mapsto Y\) буде біекція. Тоді обернена функція\(f, f^{-1}: Y \rightarrow X\), є функцією з графіком\[\{(b, a) \in Y \times X \mid(a, b) \in \operatorname{graph}(f)\} .\] Функція\(f^{-1}\) визначається «реверсом стрілок». Щоб це мало сенс, має\(f: X \rightarrow Y\) бути двооб'єктивним. Дійсно, якби не\(f\) були суб'єктивними, то був би елемент\(y\)\(Y\), який не знаходиться в діапазоні\(f\), тому не може бути відображений назад ні до чого в\(X\). \(f\)Якби не ін'єкційні, були б елементи\(z\)\(Y\), які були зображенням різних елементів\(x_{1}\) і\(x_{2}\) в\(X\). Не можна було визначити,\(f^{-1}(z)\) не вказавши, як вибрати той чи інший попередній образ. Обидві ці проблеми можна виправити. Якщо\(f\) є ін'єкційним, але не\(g: X \mapsto \operatorname{Ran}(f)\) суб'єктивним, можна визначити\[g(x)=f(x)\] для всіх\(x \in X\). Потім\(g^{-1}: \operatorname{Ran}(f) \mapsto X\). Якщо\(f\) не ін'єкційний, проблема складніша; але якщо ми можемо знайти деяку підмножину,\(X\) на якій\(f\) є ін'єкційним, ми могли б обмежити нашу увагу цим набором.
\(f\)Дозволяти бути реальною функцією\(f(x)=x^{2}\). Функція не\(f\) є біекцією, тому вона не має зворотної функції. Однак функція\[\begin{aligned} g:[0, \infty) & \rightarrow[0, \infty) \\ x & \mapsto x^{2} \end{aligned}\] є біекцією. У цьому випадку\[g^{-1}(y)=\sqrt{y} .\]
\(f\)Дозволяти бути реальною функцією,\(f(x)=e^{x}\). Ви знаєте з обчислення, що\(f\) це ін'єкція, і що\(\operatorname{Ran}(f)=\mathbb{R}^{+}\). Отже,\(f\) це не сприйняття, оскільки неявним кодоменом реальної функції є\(\mathbb{R}\). Функція\[\begin{aligned} g: \mathbb{R} & \rightarrow \mathbb{R}^{+} \\ x & \mapsto e^{x} \end{aligned}\] є біекцією та\[g^{-1}(x)=\log _{e}(x)\] попередженням: Для\(f: X \mapsto Y\) біекції ми призначили два різних значення\(f^{-1}(b)\). У Визначенні 1.31 це означає набір точок\(X\), у яких відображаються\(b\). У визначенні 1.36 це означає обернену функцію біекції\(f^{-1}\),\(f\) застосованої до точки\(b \in Y\). Однак якщо\(f\) це біекція, так що друге визначення має сенс, то ці визначення тісно пов'язані між собою. Припустимо\(a \in \operatorname{Dom}(f)\), і\(f(a)=b\). Відповідно до визначення 1.31,\(f^{-1}(b)=\{a\}\) і за визначенням\(1.36\)\(f^{-1}(b)=a\). На практиці контекст дасть зрозуміти, яке визначення призначене. ВИЗНАЧЕННЯ. Функція ідентичності, id\(\left.\right|_{X}\)\(X\) Дозволяти бути набором. Функція ідентичності on\(X\), id\(\left.\right|_{X}: X \mapsto X\), - це функція, визначена\[\left.\operatorname{id}\right|_{X}(x)=x .\] If\(f: X \rightarrow Y\) є біекцією, то\(f^{-1}\) є унікальною функцією, такою,\[f \circ f^{-1}=\left.\mathrm{id}\right|_{Y} .\] що\[f^{-1} \circ f=\left.\operatorname{id}\right|_{X}\] і Because \(f(x)=x^{2}\)не є ін'єкцією, вона не має зворотного, навіть після обмеження кодомену бути діапазоном. Тому для того, щоб «інвертувати»\(f\), ми розглянули іншу функцію\(g(x)\), яка дорівнювала\(f\) на підмножині області\(f\), і була ін'єкцією. У прикладі 1.37 ми досягли цього шляхом визначення функції\(g(x)=x^{2}\) з доменом\(\{x \in \mathbb{R} \mid x \geq 0\}\). Багато функцій, які нам потрібно інвертувати з практичних та теоретичних причин, трапляються не ін'єкціями, а отже, не мають зворотних функцій. Один із способів вирішення цієї перешкоди - розглянути функцію на меншому домені.
Враховуючи функцію,\(f: X \rightarrow Y\) ми можемо визначити «обернене»\(f\) на деякій підмножині,\(W \subseteq X\) для якої обмеження\(f\) to\(W\) є ін'єкцією.
Нехай\(f: X \rightarrow Y\) і\(W \subseteq X\). Обмеження\(f\) до\(W\), написане\(\left.f\right|_{W}\), є функція\[\begin{aligned} \left.f\right|_{W}: W & \rightarrow Y \\ x & \mapsto f(x) . \end{aligned}\] Так якщо\(f: X \rightarrow Y\) і\(W \subseteq X\), то\[\operatorname{graph}\left(\left.f\right|_{W}\right)=[W \times Y] \cap[\operatorname{graph}(f)] .\] ПРИКЛАД 1.40. Нехай\(f(x)=(x-2)^{4}\). Нехай\(W=[2, \infty)\). Потім\[\left.f\right|_{W}: W \rightarrow[0, \infty)\] йде біекція. Приклад 1.41. \(f\)Дозволяти бути реальною функцією,\(f(x)=\tan (x)\). Потім\[\operatorname{Dom}(f)=\{x \in \mathbb{R} \mid x \neq \pi / 2+k \pi, k \in \mathbb{Z}\},\] і\[\operatorname{Ran}(f)=\mathbb{R} .\] Функція\(f\) періодична з періодом\(\pi\), і тому не є ін'єкцією. Тим не менш, важливо відповісти на питання: «Під яким кутом (кутами)\(x\), чи\(\tan (x)\) дорівнює конкретне значення\(a \in \mathbb{R}\)».
Це математично еквівалентно питанню,\[\text { "What is } \arctan (a) \text { ?". }\] в обчисленні ця потреба була задоволена обмеженням домену найбільшим інтервалом,\(I\) таким, що\[\left.f\right|_{I}: I \mapsto \mathbb{R}\] Для будь-якого\(k \in \mathbb{Z}\),\[\left(\frac{(2 k+1) \pi}{2}, \frac{(2 k+3) \pi}{2}\right)\] є такий інтервал. Для того, щоб визначити конкретну функцію, вибирається найпростіший з цих інтервалів, і ми визначаємо\[\operatorname{Tan}:=\left.\tan \right|_{(-\pi / 2, \pi / 2)} .\] Спостерігати, що\[\text { Tan : }(-\pi / 2, \pi / 2) \mapsto \mathbb{R} .\] Так функція є оборотною, тобто Тан має зворотну функцію,\[\operatorname{Arctan}=\operatorname{Tan}^{-1} \text {. }\]
