6.1: Вступ до функцій
- Page ID
- 65554
Попередній перегляд діяльності 1 (Функції з попередніх курсів)
Однією з найважливіших понять у сучасній математиці є функція. У попередніх курсах математики ми часто думали про функцію як якесь правило введення-виведення, яке призначає рівно один вихід кожному входу. Таким чином, в цьому контексті, функція може бути розглянута як процедура для асоціації з кожним елементом деякого набору, називається область функції, точно один елемент іншого набору, називається codomain функції. Цю процедуру можна вважати правилом введення-виведення. Функція приймає вхід, який є елементом домену, і видає вихід, який є елементом кодомена. У численні та пречисленні входи та виходи майже завжди були дійсними числами. Отже, позначення f\(f(x) = x^2 sin x\) означає наступне:
- \(f\)це назва функції.
- \(f(x)\)є дійсним числом. Це вихід функції, коли вхід є дійсним числом\(x\). Наприклад,
\[\begin{array} {rcl} {f(\dfrac{\pi}{2})} &= & {(\dfrac{\pi}{2})^2 sin(\dfrac{\pi}{2})} \\ {} &= & {\dfrac{\pi ^2}{4} \cdot 1} \\ {} &= & {\dfrac{\pi ^2}{4}.} \end{array}\]
Для цієї функції розуміють, що область функції - це множина всіх\(\mathbb{R}\) дійсних чисел. У цій ситуації ми думаємо про домен як набір всіх можливих входів. Тобто домен - це сукупність всіх можливих дійсних чисел,\(x\) для яких може бути визначено дійсне число, що виводиться.
Це тісно пов'язане з рівнянням\(f = x^2 sin x\). З цим рівнянням ми часто розглядаємо\(x\) як вхід і\(y\) як вихід. Насправді ми іноді пишемо\(y = f(x)\). Ключ, який слід пам'ятати, полягає в тому, що функція повинна мати рівно один вихід для кожного входу. Коли ми пишемо рівняння, таке як
\(y = \dfrac{1}{2} x^3 - 1,\)
ми можемо використовувати це рівняння, щоб визначити\(y\) як функцію\(x\). Це тому, що коли ми підставляємо дійсне число для\(x\) (вхід), рівняння дає рівно одне дійсне число для\(y\) (виводу). Ми можемо дати цій функції ім'я, наприклад\(g\), і написати
\(y = g(x) = \dfrac{1}{2} x^3 - 1.\)
Однак, як написано, таке рівняння, як
\(y^2 = x + 3\)
не може бути використаний для визначення\(y\) як функції,\(x\) оскільки існують дійсні числа, які можуть бути замінені для\(x\) того, щоб отримати більше одного можливого значення\(y\). Наприклад, якщо\(x = 1\), то\(y^2 = 4\), і\(y\) може бути -2 або 2.
Яке з наведених нижче рівнянь можна використовувати для визначення функції з\(x \in \mathbb{R}\) як вхід і\(y \in \mathbb{R}\) як вихід?
- \(y = x^2 - 2\)
- \(y^2 = x + 3\)
- \(y = \dfrac{1}{2} x^3 - 1\)
- \(y = \dfrac{1}{2} x sin x\)
- \(x^2 + y^2 = 4\)
- \(y = 2x - 1\)
- \(y =dfrac{x}{x - 1}\)
Домен і кодомен функцій у Preview Activity\(\PageIndex{1}\) - це набір всіх\(\mathbb{R}\) дійсних чисел або деякої підмножини\(\mathbb{R}\). У більшості цих випадків спосіб, яким функція пов'язує елементи області з елементами кодомена, за правилом визначається деяким математичним виразом. Наприклад, коли ми говоримо,\(f\) що функція така, що
\(f(x) = \dfrac{x}{x - 1},\)
то алгебраїчне правило, яке визначає вихід функції,\(f\) коли вхід\(x\) є\(\dfrac{x}{x - 1}\). У цьому випадку ми б сказали, що область\(f\) - це множина всіх дійсних чисел, не рівних 1, оскільки ділення на нуль не визначено.
Однак поняття функції набагато більш загальне, ніж це. Домен і кодомен функції можуть бути будь-якою множиною, а спосіб, яким функція пов'язує елементи області з елементами кодомена, може мати безліч різних форм. Правилом введення-виведення для функції може бути формула, графік, таблиця, випадковий процес або словесний опис. Ми розглянемо два різних приклади в цій діяльності попереднього перегляду.
- Нехай\(b\) буде функція, яка призначає кожній людині свій день народження (місяць і день). Домен функції\(b\) - це сукупність всіх людей, а кодомен -\(b\) сукупність всіх днів у високосному році (тобто з 1 січня по 31 грудня, включаючи 29 лютого).
(а) Поясніть, чому\(b\) насправді є функцією. Ми будемо називати це функцією дня народження.
(б) У 1995 році Ендрю Уайлс прославився тим, що опублікував доказ останньої теореми Ферма. (Див. А.Д. Акцель, Остання теорема Ферма: Розблокування таємниці давньої математичної задачі, Dell Publishing, Нью-Йорк, 1996.) День народження Ендрю Уайлса - 11 квітня 1953 року. Переведіть цей факт в функціональні позначення за допомогою «функції дня народження»\(b\). Тобто заповнити пробіли для наступних знаків питання:\[b(?) = ?.\]
(c) Чи є таке твердження істинним чи хибним? Поясніть.
На кожен день\(D\) року існує людина\(x\) така, що\(b(x) = D\).
(d) Чи є таке твердження істинним чи хибним? Поясніть.
Для будь-яких людей\(x\) і\(y\), якщо\(x\) і\(y\) різні люди, то\(b(x) \ne b(y)\). - \(s\)Дозволяти функція, яка пов'язує з кожним натуральним числом суму своїх різних натуральних дільників числа. Це називається сумою функції дільників. Наприклад, натуральні дільники числа 6 - це 1, 2, 3 і 6, і так
\[\begin{array} {rcl} {s(6)} &= & {1 + 2 + 3 + 6} \\ {} &= & {12.} \end{array}\]
(а) Обчислити\(s(k)\) для кожного натурального числа\(k\) від 1 до 15.
(b) Чи існує натуральне число\(n\) таке, що\(s(n) = 5\)? Обгрунтуйте свій висновок.
(c) Чи можна знайти два різних натуральних числа\(m\) і\(n\) таке\(s(m) = s(n)\)? Поясніть.
(d) Використовуйте свої відповіді у пунктах (b) та (c), щоб визначити, чи є такі твердження істинними чи хибними.
Тобто для кожного\(m \in \mathbb{N}\) існує натуральне число\(n\) таке, що\(s(n) = m\).
II. Для всіх\(m, n \in \mathbb{N}\), якщо\(m \ne n\), то\(s(m) \ne s(n)\).
Визначення функції
Поняття функції є набагато більш загальним, ніж ідея функції, яка використовується в численні або пречислення. Зокрема, домен і кодомен не повинні бути підмножинами\(\mathbb{R}\). Крім того, спосіб, яким функція пов'язує елементи області з елементами кодомена, може мати безліч різних форм. Це правило введення-виведення може бути формулою, графіком, таблицею, випадковим процесом, комп'ютерним алгоритмом або словесним описом. Два таких приклади були введені в Preview Activity\(\PageIndex{2}\).
Для функції дня народження доменом буде набір усіх людей, а кодомен буде набором усіх днів у високосному році. Для суми функції дільників доменом є множина\(\mathbb{N}\) натуральних чисел, і кодомен також може бути\(\mathbb{N}\). В обох цих випадках правило введення-виведення було словесним описом того, як привласнити елемент кодомену елементу домену.
Формально визначимо поняття функції наступним чином:
Функція від множини\(A\) до множини\(B\) - це правило, яке пов'язує з кожним\(x\) елементом\(A\) множини рівно один елемент множини\(B\). Функція\(A\)\(B\) from to також називається відображенням від\(A\) до\(B\).
Функція позначення. Коли ми працюємо з функцією, ми зазвичай даємо їй ім'я. Ім'я часто являє собою одну букву, наприклад\(f\) або\(g\). Якщо\(f\) функція з набору,\(A\) щоб бути множиною\(B\), ми напишемо\(f: A \to B\). Це просто скорочені позначення для того, що\(f\) є функцією від множини\(A\) до множини\(B\). У цьому випадку ми також говоримо, що\(f\) карти\(A\) до\(B\).
Нехай\(f: A \to B\). (Це читається: «\(f\)Дозволяти бути функцією від\(A\) до\(B\).») \(A\)Безліч називається доменом функції\(f\), і пишемо\(A = dom(f)\). \(B\)Безліч називається кодоменом функції\(f\), і ми пишемо\(B = codom(f)\).
Якщо\(a \in A\), то елемент\(B\) того, з яким\(a\) пов'язаний, позначається\(f(a)\) і називається зображенням під\(f\). Якщо\(f(a) = b\), з\(b \in B\), то а називається преіміджем\(b\) під\(f\).
Деяка термінологія функцій з прикладом. Коли у нас є функція\(f: A \to B\), ми часто пишемо\(y = f(x)\). У цьому випадку ми\(x\) вважаємо невизначеним об'єктом, який можна вибрати з множини\(A\), і ми б сказали, що\(x\) це незалежна змінна функції\(f\) і\(y\) є залежною змінною функції\(f\).
Для конкретного прикладу розглянемо функцію\(g: \mathbb{R} \to \mathbb{R}\), де\(g(x)\) визначається за формулою
\(g(x) = x^2 - 2.\)
Зауважте, що це дійсно функція, оскільки, враховуючи будь-який вхід\(x\) у домені\(\mathbb{R}\), є рівно один вихід\(g(x)\) у codomain,\(\mathbb{R}\). Наприклад,
\[\begin{array} {rcl} {g(-2)} &= & {(-2)^2 - 2 = 2,} \\ {g(5)} &= & {5^2 - 2 = 23,} \\ {g(\sqrt 2)} &= & {(\sqrt 2)^2 - 2 = 0,} \\ {g(-\sqrt 2)} &= & {(-\sqrt 2)^2 - 2 = 0.} \end{array}\]
Так ми говоримо, що зображення -2 під\(g\) 2, зображення 5 під\(g\) 23, і так далі.
Зверніть увагу в цьому випадку, що число 0 в кодомені має два\(-\sqrt 2\) преобрази, і\(\sqrt 2\). Це не порушує математичне визначення функції, оскільки визначення лише стверджує, що кожен вхід повинен видавати один і лише один вихід. Тобто кожен елемент домену має рівно одне зображення в кодомені. Ніде визначення не передбачає, що два різних входи повинні давати різні виходи.
Знайти попередні зображення елемента в кодомені іноді може бути важко. Загалом, якщо\(y\) знаходиться в кодомені, щоб знайти його преобрази, нам потрібно запитати: «Для яких значень\(x\) в домені ми будемо мати\(y = g(x)\)?» Наприклад, для функції g, щоб знайти преобрази 5, нам потрібно знайти все\(x\) для чого\(g(x) = 5\). У цьому випадку, оскільки\(g(x) = x^2 - 2\), ми можемо це зробити, вирішивши рівняння
\(x^2 - 2 = 5.\)
Розв'язками цього рівняння є\(-\sqrt 7\) і\(\sqrt 7\). Таким чином, для функції\(g\), преобрази 5 є\(-\sqrt 7\) і\(\sqrt 7\). Ми часто використовуємо множинні позначення для цього і говоримо, що набір преобразів 5 для функції\(g\) є {\(-\sqrt 7\),\(\sqrt 7\)}.
Також зверніть увагу, що для цієї функції не кожен елемент у кодомені має попередній образ. Наприклад, немає введення\(x\) такого, що\(g(x) = -3\). Це вірно, оскільки для всіх дійсних чисел\(x\),\(x^2 \ge 0\) а значить\(x^2 - 2 \ge -2\). Це означає, що для всіх\(x\) в\(\mathbb{R}\),\(g(x) \ge -2\).
Нарешті, зауважте, що ми ввели функцію g з пропозицією «Розглянемо функцію\(g: \mathbb{R} \to \mathbb{R}\), де\(g(x)\) визначається за формулою»\(g(x) = x^2 - 2\). Це один з правильних способів зробити це, але ми часто скорочуємо це до, «Нехай\(g: \mathbb{R} \to \mathbb{R}\) буде визначено\(g(x) = x^2 - 2\)», або «Нехай\(g: \mathbb{R} \to \mathbb{R}\), де»\(g(x) = x^2 - 2\).
\(f: \mathbb{R} \to \mathbb{R}\)Дозволяти визначатися\(f(x) = x^2 - 5x\) для всіх\(x \in \mathbb{R}\). І нехай\(g: \mathbb{Z} \to \mathbb{Z}\) буде визначено\(g(m) = m^2 - 5m\) для всіх\(m \in \mathbb{Z}\).
- Визначити\(f(-3)\) і\(f(\sqrt 8)\).
- Визначити\(g(2)\) і\(g(-2)\).
- Визначте набір всіх преображений 6 для функції\(f\).
- Визначте набір всіх преображений 6 для функції\(g\).
- Визначте набір всіх попередніх зображень 2 для функції\(f\).
- Визначте набір всіх попередніх зображень 2 для функції\(g\).
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Кодомен та діапазон функції
Окрім домену та кодомена, існує ще один важливий набір, пов'язаний з функцією. Необхідність цього була проілюстрована на прикладі функції\(g\) на сторінці 285. Для цієї функції було помічено, що в кодомені є елементи, які не мають попереднього зображення або, що еквівалентно, є елементи в кодомені, які не є зображенням жодного елемента в області. Множина, про яку ми говоримо, - це підмножина кодомена, що складається з усіх зображень елементів області функції, і називається вона діапазоном функції.
Нехай\(f: A \to B\). Множина\(\{f(x)\ |\ x \in A\}\) називається діапазоном функції\(f\) і позначається range (\(f\)). Діапазон іноді\(f\) називають зображенням функції\(f\) (або зображенням\(A\) під\(f\)).
Діапазон\(f: A \to B\) може бути еквівалентно визначено наступним чином:
діапазон (\(f\))\( = \{y \in B\ |\ y = f(x) \text{ for some } x \in A\}\).
Зверніть увагу, що це означає, що range (\(f\))\(\subseteq\) codom (\(f\)) але не обов'язково означає, що range (\(f\))\(=\) codom (\(f\)). Чи маємо ми цю встановлену рівність чи ні, залежить від функції\(f\). Детальніше про це буде вивчено в розділі 6.3.
- Нехай\(b\) буде функція, яка призначає кожній людині свій день народження (місяць і день).
(a) Яка область цієї функції?
(b) Що таке кодомен для цієї функції?
(c) У попередньому перегляді діяльності ми визначили\(\PageIndex{2}\), що таке твердження вірно: Для кожного дня\(D\) року існує\(x\) така людина, яка\(b(x) = D\). Що це говорить нам про діапазон функції\(b\)? Поясніть. - \(s\)Дозволяти функція, яка пов'язує з кожним натуральним числом суму його різних натуральних числових факторів.
(a) Яка область цієї функції?
(b) Що таке кодомен для цієї функції?
(c) У Preview Activity ми визначили\(\PageIndex{2}\), що таке твердження є помилковим:
Для кожного\(m \in \mathbb{N}\) існує натуральне число\(n\) таке, що\(s(n) = m\).
Наведіть приклад натурального числа\(m\), яке показує, що це твердження є помилковим, і поясніть, що це говорить нам про діапазон функції\(s\).
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Графік реальної функції
Ми закінчимо цей розділ методами візуального донесення інформації про двох конкретних типах функцій. Перший - це знайомий метод графічних функцій, який був основною частиною деяких попередніх курсів математики. Наприклад, розглянемо функцію,\(g: \mathbb{R} \to \mathbb{R}\) визначену\(g(x) = x^2 - 2x - 1\).
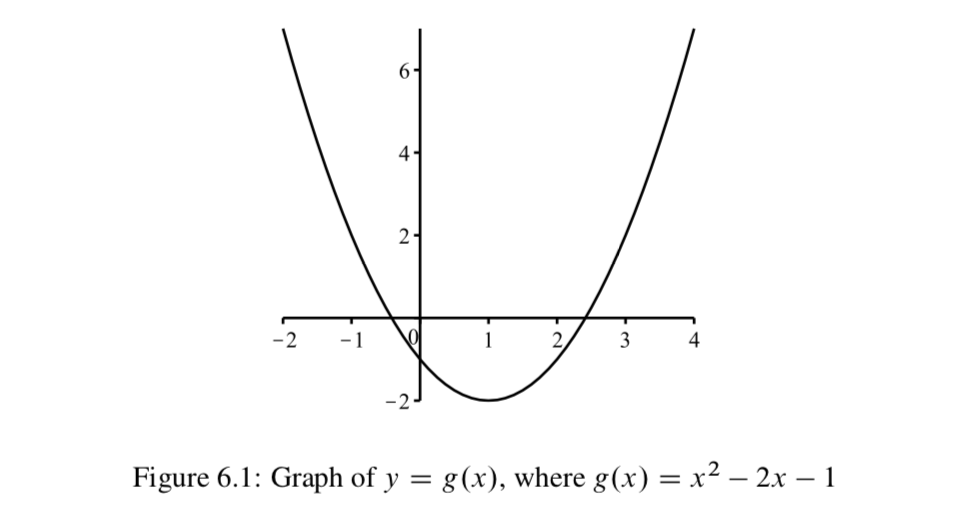
Кожна точка на цьому графіку відповідає впорядкованої парі (\(x\),\(y\)) дійсних чисел, де\(y = g(x) = x^2 - 2x - 1\). Оскільки ми використовуємо декартову площину при малюванні цього типу графа, ми можемо використовувати цей тип графа лише тоді, коли і область, і кодомен функції є підмножинами дійсних чисел\(\mathbb{R}\). Таку функцію іноді називають реальною функцією. Графік реальної функції - це наочний спосіб передачі інформації про функцію. Наприклад, діапазон\(g\) - це набір всіх значень y, які відповідають точкам на графіку. У цьому випадку граф\(g\) є параболою і має вершину в точці (1, -2). (Примітка: координату x вершини можна знайти за допомогою числення та вирішення рівняння\(f\prime (x) = 0\).) Оскільки графік функції\(g\) є параболою, ми знаємо, що візерунок показаний на лівому кінці і правому кінці графіка триває, і ми можемо зробити висновок, що діапазон\(g\) є множиною всіх\(y \in \mathbb{R}\) таких, що\(y \ge -2\). Тобто,
діапазон (\(g\))\( = \{y \in \mathbb{R}\ |\ y \ge -2\}.\)
Графік на малюнку 6.2 показує графік (трохи більше) двох повних періодів для функції\(f: \mathbb{R} \to \mathbb{R}\), де\(f(x) = Asin(Bx)\) для деяких позитивних дійсних чисел константи\(A\) і\(B\).
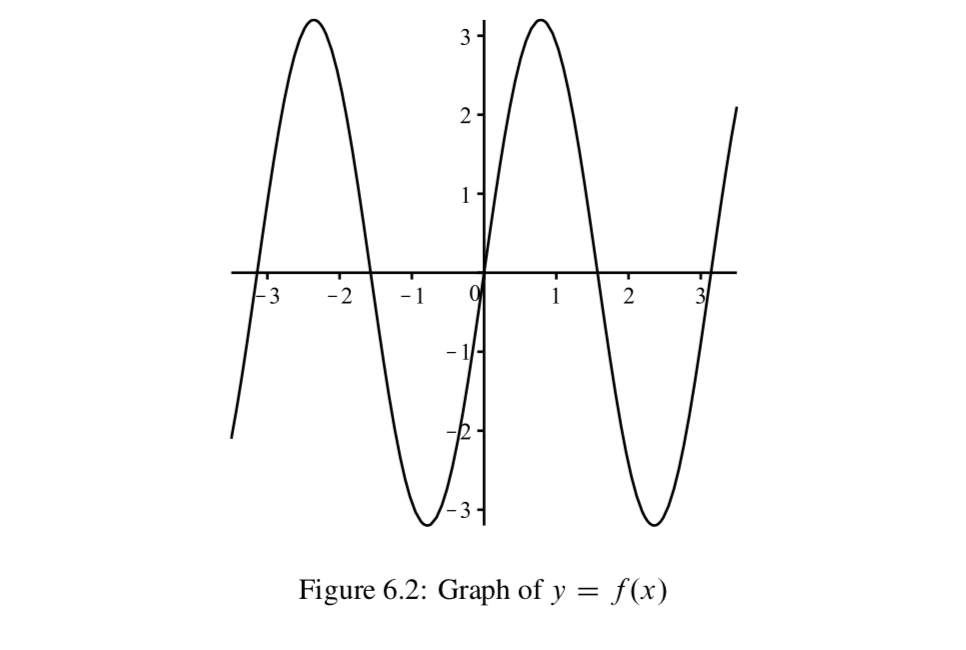
- Ми можемо використовувати графік для оцінки вихідних даних для різних входів. Це робиться шляхом оцінки\(y\) -координати для точки на графіку з заданою\(x\) -координатою. На графіку намалюйте вертикальні лінії в\(x = -1\)\(x = 2\) і і оцініть значення\(f(-1)\) і\(f(2)\).
- Аналогічно, ми можемо оцінити входи функції, які виробляють заданий вихід. Це робиться шляхом оцінки\(x\) -координат точок на графіку, які мають задану\(y\) -координату. Намалюйте горизонтальну лінію\(y = 2\) і оцініть принаймні два значення\(x\) таких, що\(f(x) = 2\).
- Скористайтеся графіком Рисунок 6.2 для оцінки діапазону функції\(f\).
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Діаграми стрілок
Іноді домен і кодомен функції є невеликими, скінченними множинами. Коли це так, ми можемо визначити функцію, просто вказавши виходи для кожного входу в домені. Наприклад, якщо ми дозволяємо\(A = \{1, 2, 3\}\) і нехай\(B = \{a, b\}\), ми можемо визначити функцію,\(F: A \to B\) вказавши, що
\(F(1) = a, F(2) = a,\text{ and } F(3) = b.\)
Це функція, оскільки кожен елемент домену зіставляється рівно з одним елементом в\(B\). Зручний спосіб ілюструвати або візуалізувати цей тип функцій - це так звана діаграма стрілок, як показано на малюнку 6.3. Діаграма зі стрілками може
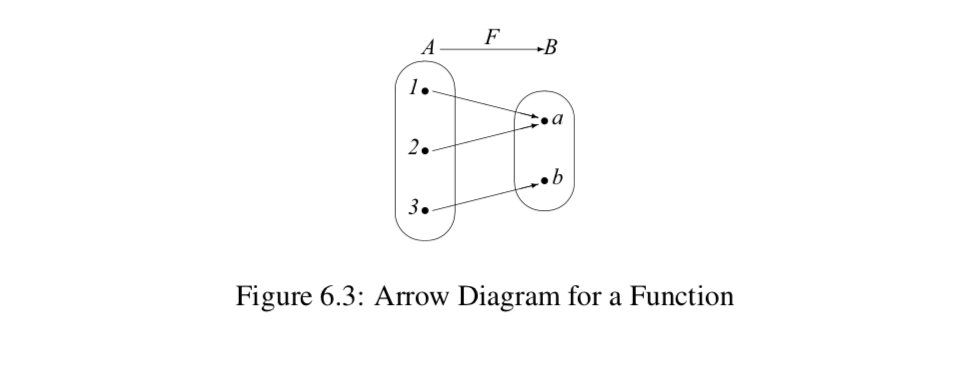
використовуватися, коли домен і кодомен функції є кінцевими (і малими). Ми представляємо елементи кожної множини точками, а потім за допомогою стрілок показуємо, як елементи домену пов'язані з елементами кодомена. Наприклад, стрілка від точки 2 в\(A\) до точки\(a\) в\(B\) являє собою той факт, що\(F(2) = a\). У цьому випадку ми можемо використовувати діаграму зі стрілками на малюнку 6.3, щоб зробити висновок, що діапазон (\(F\))\( = \{a, b\}\).
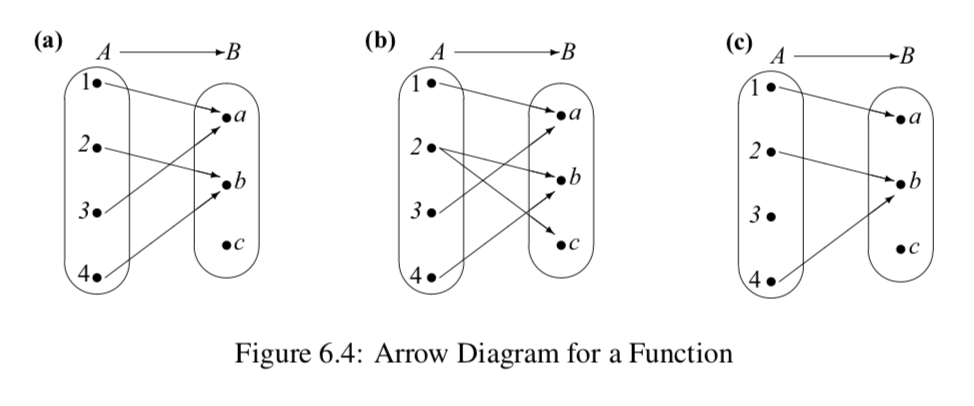
Нехай\(A = \{1, 2, 3, 4\}\) і нехай\(B = \{a, b, c\}\).
- Яку з діаграм стрілок на малюнку 6.4 можна використовувати для представлення функції від\(A\) до\(B\)? Поясніть.
- Для тих діаграм стрілок, які можна використовувати для представлення функції від\(A\) до\(B\), визначте діапазон функції.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
- Дозвольте\(f: \mathbb{R} \to \mathbb{R}\) визначитися з\(f(x) = x^2 - 2x\).
(a) Оцінювати\(f(-3)\),\(f(-1)\),\(f(1)\), і\(f(3)\).
(b) Визначте набір усіх попередніх зображень 0 та набір усіх попередніх зображень 4.
(c) Намалюйте графік функції\(f\).
(d) Визначити діапазон функції\(f\). - Нехай\(\mathbb{R} ^{\ast} = \{x \in \mathbb{R}\ |\ x \ge 0\}\), і нехай\(s: \mathbb{R} \to \mathbb{R} ^{\ast}\) будуть визначені\(s(x) = x^2\).
(a) Оцінювати\(s(-3)\),\(s(-1)\),\(s(1)\), і\(s(3)\).
(b) Визначте набір усіх попередніх зображень 0 та набір усіх попередніх зображень 2.
(c) Намалюйте графік функції\(s\).
(d) Визначити діапазон функції\(s\). - Дозвольте\(f: \mathbb{Z} \to \mathbb{Z}\) визначитися з\(f(m) = 3 - m\).
(a) Оцінювати\(f(-7)\),\(f(-3)\),\(f(3)\), і\(f(7)\).
(b) Визначте набір усіх попередніх зображень 5 та набір усіх попередніх зображень 4.
(c) Визначити діапазон функції\(f\).
(d) Цю функцію можна вважати реальною функцією, оскільки\(\mathbb{Z} \subseteq \mathbb{R}\). Намалюйте графік цієї функції. Примітка: Графік буде нескінченним набором точок, які лежать на прямій. Однак це не буде лінією, оскільки її домен не є,\(\mathbb{R}\) але є\(\mathbb{Z}\). - Дозвольте\(f: \mathbb{Z} \to \mathbb{Z}\) визначитися з\(f(m) = 2m + 1\).
(a) Оцінювати\(f(-7)\),\(f(-3)\),\(f(3)\), і\(f(7)\).
(b) Визначте набір усіх попередніх зображень 5 та набір усіх попередніх зображень 4.
(c) Визначити діапазон функції\(f\).
(d) Намалюйте графік функції\(f\). Дивіться коментарі у Вправі (3d). - Нагадаємо, що реальна функція - це функція, домен і кодомен якої є підмножинами дійсних чисел R. (Див. стор. 288.) Більшість функцій, що використовуються в обчисленні, є реальними функціями. Досить часто реальна функція задається формулою або графіком без конкретного посилання на домен або кодомен. У цих випадках звичайною умовою є припущення, що область дійсної функції\(f\) - це набір всіх дійсних чисел,\(x\) для яких\(f(x)\) є дійсним числом, і що кодомен є\(\mathbb{R}\). Наприклад, якщо ми визначимо (реальну) функцію\(f\),
\[f(x) = \dfrac{x}{x - 2},\]
ми будемо припускати, що домен є набором всіх дійсних чисел, які не рівні 2 і що codomain в\(\mathbb{R}\).
Визначте область і діапазон кожної з наступних реальних функцій. Це може допомогти використовувати графічний калькулятор для побудови графіка функції.
(a) Функція,\(k\) визначена\(k(x) = \sqrt{x - 3}\)
(b) Функція,\(F\) визначена\(F(x) = ln(2x - 1)\)
(c) Функція,\(f\) визначена\(f(x) = 3sin(2x)\)
(d) Функція,\(g\) визначена \(g(x) = \dfrac{4}{x^2 - 4}\)
(e) Функція,\(G\) визначена\(G(x) = 4cos(\pi x) + 8\) - Число дільників функції. \(d\)Дозволяти функція, яка пов'язує з кожним натуральним числом число його натуральних дільників. Саме\(d: \mathbb{N} \to \mathbb{N}\) там\(d(n)\) знаходиться число натуральних дільників числа\(n\). Наприклад,\(d(6) = 4\) оскільки 1, 2, 3 і 6 є натуральними числовими дільниками 6.
(а) Обчислити\(d(k)\) для кожного натурального числа\(k\) від 1 до 12.
(b) Чи існує натуральне число\(n\) таке, що\(d(n) = 1\)? Що таке сукупність передзображень натурального числа 1.
(c) Чи існує натуральне число\(n\) таке, що\(d(n) = 2\)? Якщо так, то визначте множину всіх преобразів натурального числа 2.
(d) Чи є таке твердження істинним чи хибним? Обгрунтуйте свій висновок.
Для всіх\(m, n \in \mathbb{N}\), якщо\(m \ne n\), то\(d(m) \ne d(n)\).
(e) Обчислити\(d(2^k)\) для\(k = 0\) і для кожного натурального числа\(k\) від 1 до 6.
(f) На основі вашої роботи у Вправі (6e) зробіть гіпотезу для формули,\(d(2^n)\) де\(n\) є невід'ємне ціле число. Тоді поясніть, чому ваша здогадка правильна.
(g) Чи є таке твердження істинним чи хибним?
Для кожного\(n \in \mathbb{N}\) існує натуральне число\(m\) таке, що\(d(m) = n\). - У Вправі (6) ми ввели функцію числа дільників\(d\). Для цієї функції\(d: \mathbb{N} \to \mathbb{N}\),\(d(n)\) де число натуральних дільників числа\(n\).
Функція, яка пов'язана з цією функцією, - це так звана множина дільників функції. Це можна визначити як функцію\(S\), яка пов'язує з кожним натуральним числом безліч його різних натуральних числових факторів. Наприклад,\(S(6) = \{1, 2, 3, 6\}\) і\(S(10) = \{1, 2, 5, 10\}\).
(a) Обговоріть функцію\(S\), ретельно вказавши її домен, кодомен та її правило для визначення результатів.
(b) Визначити\(S(n)\) принаймні п'ять різних значень\(n\).
(c) Визначити\(S(n)\) принаймні три різних простих числових значень\(n\).
(d) Чи існує натуральне число,\(n\) таке, що карта (\(S(n) = 1\))? Поясніть. [Нагадаємо, що card (\(S(n)\)) - це кількість елементів у наборі\(S(n)\).]
(e) Чи існує натуральне число,\(n\) таке, що карта (\(S(n) = 2\))? Поясніть.
(f) Запишіть висновок для функції з\(d\) точки зору виводу для функції\(S\). Тобто пишіть\(d(n)\) в терміні\(S(n)\).
(g) Чи є таке твердження істинним чи хибним? Обгрунтуйте свій висновок.
Для всіх натуральних чисел\(m\) і\(n\), якщо\(m \ne n\), то\(S(m) \ne S(n)\).
(h) Чи є таке твердження вірним чи хибним? Обгрунтуйте свій висновок.
Для всіх множин\(T\), які є\(\mathbb{N}\) підмножинами, існує натуральне число\(n\) таке, що\(S(n) = T\).
Дослідження та діяльність - Створення функцій з скінченними доменами. Нехай\(A = \{a, b, c, d\}\),\(B= \{a, b, c\}\). і\(C = \{s, t, u, v\}\). У кожному з наступних вправ намалюйте діаграму зі стрілками, щоб представити вашу функцію, коли це доречно.
(a) Створіть функцію, діапазон\(f: A \to C\) якої є множиною,\(C\) або поясніть, чому неможливо побудувати таку функцію.
(b) Створіть функцію, діапазон\(f: A \to C\) якої є множиною,\(\{u,v\}\) або поясніть, чому неможливо побудувати таку функцію.
(c) Створіть функцію, діапазон\(f: B \to C\) якої є множиною,\(C\) або поясніть, чому неможливо побудувати таку функцію.
(d) Створіть функцію, діапазон\(f: A \to C\) якої є множиною,\(\{u\}\) або поясніть, чому неможливо побудувати таку функцію.
(e) Якщо можливо, створіть функцію,\(f: A \to C\) яка задовольняє такій умові:
Для всіх\(x,y \in A\), якщо\(x \ne y\), то\(f(x) \ne f(y)\).
Якщо створити таку функцію не представляється можливим, поясніть, чому.
(f) Якщо можливо, створіть функцію,\(f: A \to \{s, t, u\}\) яка задовольняє такій умові:
Для всіх\(x,y \in A\), якщо\(x \ne y\), то\(f(x) \ne f(y)\).
Якщо створити таку функцію не представляється можливим, поясніть, чому.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
